| Citation: | Kamal Shah, Arshad Ali, M. Boukhobza, A. Debbouche, Thabet Abdeljawad. HYERS-ULAM STABILITY ANALYSIS FOR PIECEWISE VARIABLE ORDER FRACTIONAL IMPULSIVE EVOLUTION SYSTEMS[J]. Journal of Applied Analysis & Computation, 2025, 15(5): 3159-3184. doi: 10.11948/20240536 |
HYERS-ULAM STABILITY ANALYSIS FOR PIECEWISE VARIABLE ORDER FRACTIONAL IMPULSIVE EVOLUTION SYSTEMS
-
Abstract
We investigate a class of piecewise variable-order fractional differential equations with impulsive and nonlocal conditions in Banach space. The nonhomogeneous term in the proposed system is given in terms of variable kernel which has flexibility property. We formulate appropriate equivalent integral equations to the considered evolution problem, then we show the solvability results by using mainly fractional calculus and fixed point techniques. Further, we study Hyers-Ulam stability analysis by adapting suitable conditions. The concerned area has numerous applications in those evolution processes and phenomenon, where abrupt changes occur. At the end, we support our obtained theory by illustrative and computational example.
-

-
References
[1] T. Abdeljawad, N. Mlaiki and M. S. Abdo, Caputo-type fractional systems with variable order depending on the impulses and changing the kernel, Fractals, 2022, 30(8), 2240219. doi: 10.1142/S0218348X22402198 [2] Z. Ahmad, F. Ali, A. M. Alqahtani, N. Khan and I. Khan, Dynamics of cooperative reactions based on chemical kinetics with reaction speed: A comparative analysis with singular and nonsingular kernels, Fractals, 2022, 30(01), 2240048. doi: 10.1142/S0218348X22400485 [3] Z. Ahmad, G. Bonanomi, A. Cardone, A. Iuorio, G. Toraldo and F. Giannino, Fractal-fractional sirs model for the disease dynamics in both prey and predator with singular and nonsingular kernels, Journal of Biological Systems, 2024, 32(04), 1487–1520. doi: 10.1142/S0218339024400035 [4] Z. Ahmad, G. Bonanomi, D. di Serafino and F. Giannino, Transmission dynamics and sensitivity analysis of pine wilt disease with asymptomatic carriers via fractal-fractional differential operator of Mittag-Leffler kernel, Applied Numerical Mathematics, 2023, 185, 446–465. doi: 10.1016/j.apnum.2022.12.004 [5] Z. Ahmad, S. Crisci, S. Murtaza and G. Toraldo, Numerical insights of fractal-fractional modeling of magnetohydrodynamic Casson hybrid nanofluid with heat transfer enhancement, Mathematical Methods in the Applied Sciences, 2024, 47(11), 9046–9066. doi: 10.1002/mma.10059 [6] A. Ali, K. J. Ansari, H. Alrabaiah, A. Aloqaily and N. Mlaiki, Coupled system of fractional impulsive problem involving power-law kernel with piecewise order, Fractal Fract. 2023, 7(6), 436. doi: 10.3390/fractalfract7060436 [7] R. Almeida, A Caputo fractional derivative of a function with respect to another function, Commun. Nonlinear Sci. Numer. Simul., 2017, 44, 460–481. doi: 10.1016/j.cnsns.2016.09.006 [8] J. Alzabut, M. Houas and M. I. Abbas, Application of fractional quantum calculus on coupled hybrid differential systems within the sequential Caputo fractional q-derivatives, Demonstratio Mathematica, 2023, 56(1), 20220205. doi: 10.1515/dema-2022-0205 [9] K. J. Ansari, Asma, F. Ilyas, K. Shah, A. Khan and T. Abdeljawad, On new updated concept for delay differential equations with piecewise Caputo fractional-order derivative, Waves in Random and Complex Media, 2023, 2023, 1–20. [10] A. Atangana and D. Baleanu, New fractional derivatives with nonlocal and non-singular kernel: Theory and application to heat transfer model, Thermal Science, 2016, 20(2), 763–769. doi: 10.2298/TSCI160111018A [11] K. Balachandran and S. Kiruthika, Existence of solutions of abstract fractional impulsive semilinear evolution equations, Electronic Journal of Qualitative Theory of Differential Equations, 2010, 4, 1–12. [12] M. Bragdi, A. Debbouche and D. Baleanu, Existence of solutions for fractional differential inclusions with separated boundary conditions in Banach space, Advances in Mathematical Physics, 2013, 426061. [13] L. Byszewski and V. Lakshmikantham, Theorem about the existence and uniqueness of a solution of a nonlocal abstract Cauchy problem in a Banach space, Applicable Analysis, 1991, 40(1), 11–19. doi: 10.1080/00036819008839989 [14] M. Caputo and M. Fabrizio, A new definition of fractional derivative without singular kernel, Progress in Fractional Differentiation and Applications, 2015, 1(2), 73–85. [15] A. Debbouche and J. J. Nieto, Relaxation in controlled systems described by fractional integro-differential equations with nonlocal control conditions, Electronic Journal of Differential Equations, 2015, 2015(89), 1–18. [16] M. Du, Z. Wang and H. Hu, Measuring memory with the order of fractional derivative, Scientific Reports, 2013, 3(1), 1–3. [17] L. L. Huang, J. H. Park, G. C. Wu and Z. W. Mo, Variable-order fractional discrete-time recurrent neural networks, J. Comput. Appli. Math., 2020, 370, 112633. doi: 10.1016/j.cam.2019.112633 [18] A. Jajarmi, D. Baleanu, K. Zarghami Vahid and S. Mobayen, A general fractional formulation and tracking control for immunogenic tumor dynamics, Mathematical Methods in the Applied Sciences, 2022, 45, 667–680. doi: 10.1002/mma.7804 [19] K. Karthikeyan, A. Debbouche and D. F. M. Torres, Analysis of Hilfer fractional integro-differential equations with almost sectorial operators, Fractal and Fractional, 2021, 5(1), 22. doi: 10.3390/fractalfract5010022 [20] A. Khan, J. F. Gómez-Aguilar, T. S. Khan and H. Khan, Stability analysis and numerical solutions of fractional order HIV/AIDS model, Chaos, Solitons Fractals, 2019, 122, 119–128. doi: 10.1016/j.chaos.2019.03.022 [21] H. Khan, J. Alzabut, D. Baleanu, G. Alobaidi and M. U. Rehman, Existence of solutions and a numerical scheme for a generalized hybrid class of n-coupled modified ABC-fractional differential equations with an application, AIMS Mathematics, 2023, 8(3), 6609–6625. doi: 10.3934/math.2023334 [22] H. Khan, W. Chen, A. Khan, T. S. Khan and Q. M. Al-Madlal, Hyers-Ulam stability and existence criteria for coupled fractional differential equations involving p-Laplacian operator, Advances in Difference Equations, 2018, 2018, 1–16. doi: 10.1186/s13662-017-1452-3 [23] A. A. Kilbas, H. M. Srivastava and J. J. Trujillo, Theory and Applications of Fractional Differential Equations, Elsevier, Amsterdam, 2006. [24] H. Kim, R. Sakthivel, A. Debbouche and D. F. M. Torres, Traveling wave solutions of some important Wick-type fractional stochastic nonlinear partial differential equations, Chaos, Solitons & Fractals, 2020, 131, 109542. [25] S. Kumar, R. Kumar, M. S. Osman and B. Samet, A wavelet based numerical scheme for fractional order SEIR epidemic of measles by using Genocchi polynomials, Numerical Methods for Partial Differential Equations, 2021, 37(2), 1250–1268. doi: 10.1002/num.22577 [26] V. Lakshmikantham and A. Vatsala, Basic theory of frac-tional differential equations, Nonlinear Analysis: Theory, Methods & Applications, 2008, 69(8), 2677–2682. [27] V. Lakshimikantham and A. Vatsala, Theory of fractional differential inequalities and applications, Communications in Applied Analysis, 2007, 11, 395–402. [28] X. Liao, T. Zhou, L. Zhang, X. Hu and Y. Peng, A method for calculating the derivative of activation functions based on piecewise linear approximation, Electronics, 2023, 12(2), 267. doi: 10.3390/electronics12020267 [29] B. Maayah, A. Moussaoui, S. Bushnaq and O. Abu Arqub, The multistep Laplace optimized decomposition method for solving fractional-order coronavirus disease model (COVID-19) via the Caputo fractional approach, Demonstratio Mathematica, 2022, 55(1), 963–977. doi: 10.1515/dema-2022-0183 [30] R. L. Magin, Fractional calculus in bioengineering-part 2, Crit. Rev. Biomed. Eng., 2004, 32(2), 105–193. doi: 10.1615/CritRevBiomedEng.v32.i2.10 [31] C. McCluskey, A model of HIV/AIDS with staged progression and amelioration, Math Bio., 2003, 181, 1–16. doi: 10.1016/S0025-5564(02)00149-9 [32] M. Mohammad, M. Sweidan and A. Trounev, Piecewise fractional derivatives and wavelets in epidemic modeling, Alexandria Engineering Journal, 2024, 101, 245–253. doi: 10.1016/j.aej.2024.05.053 [33] Y. A. Rossikhin and M. V. Shitikova, Applications of fractional calculus to dynamic problems of linear and nonlinear hereditary mechanics of solids, Appl. Mech. Rev., 1997, 50, 15–67. doi: 10.1115/1.3101682 [34] S. G. Samko, A. A. Kilbas and O. I. Marichev, Fractional Integrals and Derivatives, Theory and Applications, Gordon & Breach, Amsterdam, The Netherlands, 1993. [35] H. Schaefer, Über die methode der a priori-Schranken, Math. Ann., 1955, 129, 415–416. doi: 10.1007/BF01362380 [36] K. Shah, T. Abdeljawad and A. Ali, Mathematical analysis of the Cauchy type dynamical system under piecewise equations with Caputo fractional derivative, Chaos, Solitons & Fractals, 2022, 161, 112356. [37] K. Shah, A. Ullah and J. J. Nieto, Study of fractional order impulsive evolution problem under nonlocal Cauchy conditions, Math. Method. Appl. Sci., 2021, 44(11), 8516–8527. doi: 10.1002/mma.7274 [38] G. C. Wu, Z. G. Deng, D. Baleanu and D. Q. Zeng, New variable-order fractional chaotic systems for fast image encryption, Chaos, 2019, 29, 083103. doi: 10.1063/1.5096645 [39] G. C. Wu, M. Luo, L. L. Huang and S. Banerjee, Short memory fractional differential equations for new memristor and neural network design, Nonlinear Dynamics, 2020, 100(4), 3611–3623. doi: 10.1007/s11071-020-05572-z [40] G. C. Wu, D. Q. Zeng and D. Baleanu, Fractional impulsive differential equations: Exact solutions, integral equations and short memory case, Fractional Calculus and Applied Analysis, 2019, 22, 180–192. doi: 10.1515/fca-2019-0012 [41] A. Zeb, A. Atangana, Z. Khan and S. Djillali, A robust study of a piecewise fractional order COVID-19 mathematical model, Alexandria Engineering Journal, 2022, 61(7), 5649–5665. doi: 10.1016/j.aej.2021.11.039 -
-
-
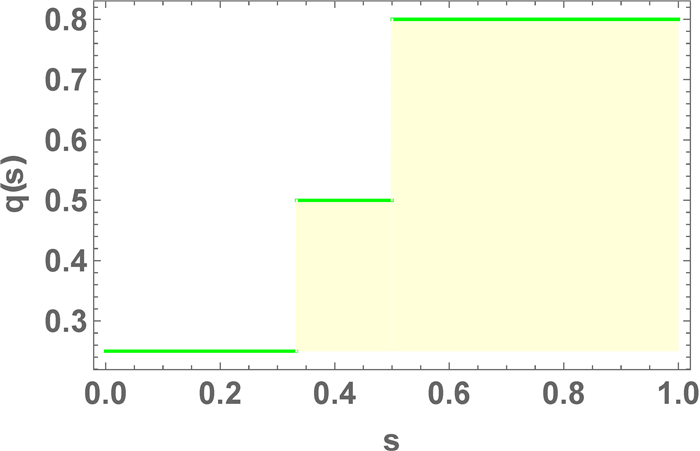
Figure 1.
Graphical presentation of
$ {q} $ -
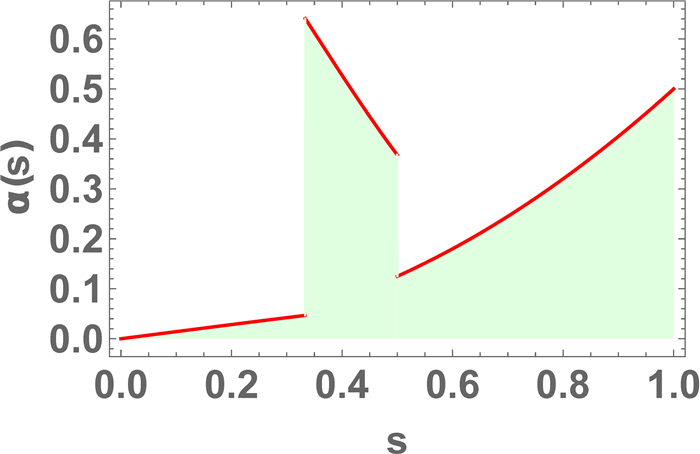
Figure 2.
Graphical presentation of
$ \alpha $ -
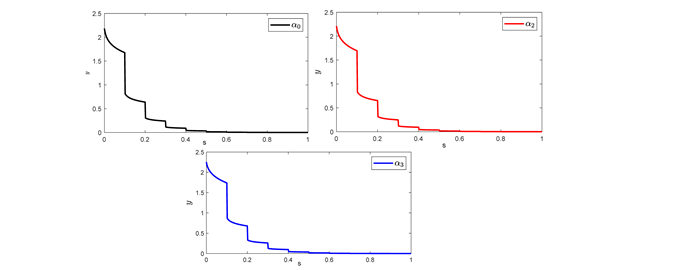
Figure 3.
Graphical presentation of solution of Problem 5.1.




 DownLoad:
DownLoad: