| Citation: | Junyan Bao, Peiguang Wang. SHEAF IMPULSIVE FUZZY CONTROL PROBLEM UNDER THE SECOND TYPE HUKUHARA DERIVATIVE[J]. Journal of Applied Analysis & Computation, 2025, 15(5): 2900-2920. doi: 10.11948/20240505 |
SHEAF IMPULSIVE FUZZY CONTROL PROBLEM UNDER THE SECOND TYPE HUKUHARA DERIVATIVE
-
Abstract
The concept of sheaf-solution to impulsive fuzzy control differential equations under the second-type Hukuhara derivative is developed in this paper. The continuous dependence of the sheaf-solution of such equations on the initial value is investigated using the Gronwall inequality. In addition, the comparison theorem and the criteria for the stability for the impulsive fuzzy control differential equations are provided.
-

-
References
[1] P. Balasubramaniam and S. Muralisankar, Existence and uniqueness of fuzzy solution for the nonlinear fuzzy integrodifferential equations, Applied Mathematics Letters, 2001, 14(4), 455–462. doi: 10.1016/S0893-9659(00)00177-4 [2] B. Bede and S. G. Gal, Generalizations of the differentiability of fuzzy-number-value functions with applications to fuzzy differential equations, Fuzzy Sets and Systems, 2005, 151, 581–599. doi: 10.1016/j.fss.2004.08.001 [3] B. Bede and S. G. Gal, Almost periodic fuzzy-number-valued functions, Fuzzy Sets and Systems, 2004, 147, 385–403. doi: 10.1016/j.fss.2003.08.004 [4] Y. C. Canoa and H. R. Flores, On new solutions of fuzzy differential equations, Chaos, Solitons and Fractals, 2008, 38, 112–119. doi: 10.1016/j.chaos.2006.10.043 [5] Z. Ding, M. Ma and A. Kandel, Existence of the solutions of fuzzy differential equations with parameters, Information Sciences, 1997, 99(3–4), 205–217. doi: 10.1016/S0020-0255(96)00279-4 [6] S. H. Hong, J. Gao and Y. Z. Peng, Solvability and stability of impulsive set dynamic equations on time scales, Abstract and Applied Analysis, 2014, 1, 610365. [7] J. Z. Huang and D. F. Luo, Ulam-Hyers stability of fuzzy fractional non-instantaneous impulsive switched differential equations under generalized Hukuhara differentiability, International Journal of Fuzzy Systems, 2024, 26(5), 1481–1492. doi: 10.1007/s40815-024-01681-8 [8] V. Lakshmikantham and S. Leela, Differential and Integral Inequalities, Vol. 1, Academic Press, New York, 1969. [9] V. Lakshmikantham and S. G. Leela, Stability theory of fuzzy differential equations via differential inequalities, Mathematical Inequalities & Applications, 1999, 2(4), 551–559. [10] V. Lakshmikantham and R. N. Mohapatra, Theory of Fuzzy Differential Equations and Inclusions, Taylor and Francis Publishers, London, 2003. [11] R. Liu, J. R. Wang and D. O'Regan, Ulam type stability of first-order linear impulsive fuzzy differential equations, Fuzzy Sets and Systems, 2020, 400, 34–89. doi: 10.1016/j.fss.2019.10.007 [12] D. F. Luo, X. Wang, T. Caraballo and Q. X. Zhu, Ulam-Hyers stability of Caputo-type fractional fuzzy stochastic differential equations with delay, Communications in Nonlinear Science and Numerical Simulation, 2023, 121, 107229. doi: 10.1016/j.cnsns.2023.107229 [13] J. J. Nieto, A. Khastan and K. Ivaz, Numerical solution of fuzzy differential equations under generalized differentiability, Nonlinear Analysis: Hybrid Systems, 2009, 3(4), 700–707. doi: 10.1016/j.nahs.2009.06.013 [14] J. J. Nieto, Rodríguez-López and Rosana, Existence and uniqueness results for fuzzy differential equations subject to boundary value conditions, American Institute of Physics Conference Series, American Institute of Physics, 2009, 264–273. [15] D. A. Ovsanikov, Mathematical Methods for Sheaf-Control, Publisher of Leningrad University, Leningrad, 1980. [16] X. Pan, Robust stability of fuzzy impulsive differential equations with delay, International Mathematical Forum, 2011, 60(6), 2985–2996. [17] N. D. Phu and N. V. Hoa, Mittag-Leffler stability of random-order fractional nonlinear uncertain dynamic systems with impulsive effects, Nonlinear Dynamics, 2023, 111(10), 9409–9430. doi: 10.1007/s11071-023-08340-x [18] N. D. Phu and T. T. Tung, Some results on sheaf-solutions of sheaf set control problems, Nonlinear Analysis: Theory, Methods & Applications, 2007, 67, 1309–1315. [19] N. D. Phu and T. T. Tung, Some properties of sheaf-solutions of sheaf fuzzy control problems, Electronic Journal of Differential Equations, 2006, 108, 1–8. [20] M. Puri and D. Ralescu, Differentials of fuzzy functions, Journal of Mathematical Analysis and Applications, 1983, 91, 552–558. doi: 10.1016/0022-247X(83)90169-5 [21] S. Seikkala, On the fuzzy initial value problem, Fuzzy Sets and Systems, 1987, 24, 319–330. doi: 10.1016/0165-0114(87)90030-3 [22] Y. H. Shen, Hyers-Ulam-Rassias stability of first order linear partial fuzzy differential equations under generalized differentiability, Advances in Difference Equations, 2015, 1, 351. [23] S. Song and C. Wu, Existence and uniqueness of solutions to Cauchy problem of fuzzy differential equations, Fuzzy Sets and Systems, 2000, 110(1), 55–67. doi: 10.1016/S0165-0114(97)00399-0 [24] L. Stefanini, A Generalization of Hukuhara Difference and Division for Interval and Fuzzy Arithmetic, Soft Methods for Handling Variability and Imprecision, Springer Berlin Heidelberg, 2008. [25] L. Stefanini and B. Bede, Generalized Hukuhara differentiability of interval-valued functions and interval differential equations, Nonlinear Analysis: Theory, Methods & Applications, 2009, 71, 1311–1328. [26] P. V. Tri, N. V. Hoa and N. D. Phu, Sheaf fuzzy problems for functional differential equations, Advances in Difference Equations, 2014, 1, 156. [27] V. A. Truong and V. H. Hoa, Fuzzy differential equations with Riemann-Liouville generalized fractional integrable impulses, Fuzzy Sets and Systems, 2022, 429, 74–100. doi: 10.1016/j.fss.2021.01.001 [28] A. S. Vatsala, Impulsive hybrid fuzzy differential equation, Facta Universitatis, Series: Mechanics, Automatic Control and Robotics, 2003, 3(14), 851–859. [29] H. Vu and N. V. Hoa, On impulsive fuzzy functional differential equations, Iranian Journal of Fuzzy Systems, 2016, 13(4), 79–94. [30] X. Wang, D. F. Luo and Q. X. Zhu, Ulam-Hyers stability of Caputo type fuzzy fractional differential equations with time-delays, Chaos Solitons & Fractals, 2022, 156, 111822. -
-
-
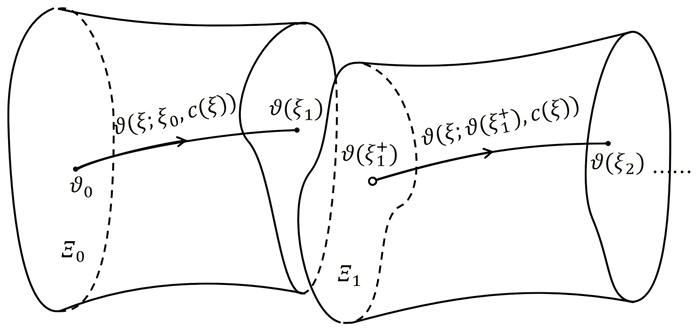
Figure 1.
Sheaf-solution
$ \Xi_{\xi, c}$




 DownLoad:
DownLoad: