| Citation: |
Yanjuan Yang, Jin Zhao. SYMMETRY OF ROTATIONAL EQUATORIAL INTERNAL WAVES[J]. Journal of Applied Analysis & Computation, 2025, 15(4): 2461-2473. doi: 10.11948/20240514
|
SYMMETRY OF ROTATIONAL EQUATORIAL INTERNAL WAVES
-
Abstract
The aim of this paper is to study the symmetry of the equatorial internal waves, which propagate above the thermocline and beneath the upper flat boundary. For general vorticity distributions, we prove that a steady periodic internal wave with a monotone profile between crests and troughs must be symmetric. Moreover, for the flows with constant vorticity, we show that the symmetric periodic internal waves must be traveling waves.
-
-
References
[1] A. A. Abrashkin and A. Constantin, A steady azimuthal stratified flow modelling the antarctic circumpolar current, J. Differential Equations, 2023, 374, 632–641. doi: 10.1016/j.jde.2023.07.044 [2] A. Aivaliotis, On the symmetry of equatorial travelling water waves with constant vorticity and stagnation points, Nonlinear Anal. Real World Appl., 2017, 34, 159–171. doi: 10.1016/j.nonrwa.2016.08.010 [3] B. Basu, On the nonlinear three-dimensional models in equatorial ocean flows, Commun. Pure Appl. Anal., 2022, 21(7), 2271–2290. doi: 10.3934/cpaa.2022085 [4] J. Chu, Q. Ding and Y. Yang, Steady periodic waves and formal stability for fixed-depth rotational equatorial flows, J. Differential Equations, 2020, 269(5), 4192–4214. doi: 10.1016/j.jde.2020.03.040 [5] J. Chu and J. Escher, Steady periodic equatorial water waves with vorticity, Discrete Cont. Dyn. Syst., 2019, 39(8), 4713–4729. doi: 10.3934/dcds.2019191 [6] J. Chu and L. Wang, Analyticity of rotational travelling waves in two-layer flows, Stud. Appl. Math., 2021, 146(3), 605–634. doi: 10.1111/sapm.12358 [7] J. Chu and Y. Yang, Constant vorticity water flows in the equatorial $\beta$-plane approximation with centripetal forces, J. Differential Equations, 2020, 269(11), 9336–9347. doi: 10.1016/j.jde.2020.06.044 CrossRef $\beta$-plane approximation with centripetal forces" target="_blank">Google Scholar
[8] A. Constantin, The trajectories of particles in Stokes waves, Invent. Math., 2006, 166(3), 523–535. doi: 10.1007/s00222-006-0002-5 [9] A. Constantin, On the modelling of equatorial waves, Geophys. Res. Lett., 2012, 39(5), L05602. [10] A. Constantin, Mean velocities in a Stokes wave, Arch. Ration. Mech. Anal., 2013, 207(3), 907–917. doi: 10.1007/s00205-012-0584-6 [11] A. Constantin, Some nonlinear, equatorially trapped, nonhydrostatic internal geophysical waves, J. Phys. Oceanogr., 2014, 44(2), 781–789. doi: 10.1175/JPO-D-13-0174.1 [12] A. Constantin, M. Ehrnström and E. Wahlén, Symmetry of steady periodic gravity water waves with vorticity, Duke Math. J., 2007, 140(3), 591–603. [13] A. Constantin and J. Escher, Symmetry of steady periodic surface water waves with vorticity, J. Fluid Mech., 2004, 498, 171–181. doi: 10.1017/S0022112003006773 [14] A. Constantin and J. Escher, Symmetry of steady deep-water waves with vorticity, European J. Appl. Math., 2004, 15(6), 755–768. doi: 10.1017/S0956792504005777 [15] A. Constantin and J. Escher, Analyticity of periodic traveling free surface water waves with vorticity, Ann. of Math. (2), 2011, 173(1), 559–568. doi: 10.4007/annals.2011.173.1.12 [16] A. Constantin and R. I. Ivanov, Equatorial wave-current interactions, Comm. Math. Phys., 2019, 370(1), 1–48. doi: 10.1007/s00220-019-03483-8 [17] A. Constantin and R. S. Johnson, The dynamics of waves interacting with the equatorial undercurrent, Geophys. Astrophys. Fluid Dyn., 2015, 109(4), 311–358. doi: 10.1080/03091929.2015.1066785 [18] A. Constantin and W. Strauss, Exact steady periodic water waves with vorticity, Comm. Pure Appl. Math., 2004, 57(4), 481–527. doi: 10.1002/cpa.3046 [19] A. Constantin and W. Strauss, Pressure beneath a Stokes wave, Comm. Pure Appl. Math., 2010, 63(4), 533–557. doi: 10.1002/cpa.20299 [20] A. Constantin, W. Strauss and E. Varvaruca, Global bifurcation of steady gravity water waves with critical layers, Acta Math., 2016, 217(2), 195–262. doi: 10.1007/s11511-017-0144-x [21] W. Craig and P. Sternberg, Symmetry of solitary waves, Comm. Partial Differential Equations, 1988, 13(5), 603–633. doi: 10.1080/03605308808820554 [22] M. Ehrnstrom, Deep-water waves with vorticity: Symmetry and rotational behaviour, Discrete Contin. Dyn. Syst., 2007, 19(3), 483–491. doi: 10.3934/dcds.2007.19.483 [23] M. Ehrnstrom, H. Holden and X. Raynaud, Symmetric waves are traveling waves, Int. Math. Res. Not. IMRN, 2009, 24, 4578–4596. [24] L. E. Fraenkel, An Introduction to Maximum Principles and Symmetry in Elliptic Problems, Cambridge University Press, Cambridge, 2000. [25] B. Gidas, W. Ni and L. Nirenberg, Symmetry and related properties via the maximum principle, Comm. Math. Phys., 1979, 68(3), 209–243. doi: 10.1007/BF01221125 [26] D. Henry, Analyticity of the streamlines for periodic travelling free surface capillary-gravity water waves with vorticity, SIAM J. Math. Anal., 2010, 42(6), 3103–3111. doi: 10.1137/100801408 [27] D. Henry, Large amplitude steady periodic waves for fixed-depth rotational flows, Comm. Partial Differential Equations, 2013, 38(6), 1015–1037. doi: 10.1080/03605302.2012.734889 [28] D. Henry, A modified equatorial β-plane approximation modelling nonlinear wave-current interactions, J. Differential Equations, 2017, 263(5), 2554–2566. doi: 10.1016/j.jde.2017.04.007 [29] D. Henry, Energy considerations for nonlinear equatorial water waves, Commun. Pure Appl. Anal., 2022, 21(7), 2337–2356. doi: 10.3934/cpaa.2022057 [30] D. Henry and H.-C. Hsu, Instability of equatorial water waves in the $f$-plane, Discrete Contin. Dyn. Syst., 2015, 35(3), 909–916. doi: 10.3934/dcds.2015.35.909 [31] D. Henry and A.-V. Matioc, On the symmetry of steady equatorial wind waves, Nonlinear Anal. Real World Appl., 2014, 18, 50–56. doi: 10.1016/j.nonrwa.2014.01.009 [32] D. Henry and G. Villari, Flow underlying coupled surface and internal waves, J. Differential Equations, 2022, 310, 404–442. doi: 10.1016/j.jde.2021.11.009 [33] V. H. Hur, Symmetry of steady periodic water waves with vorticity, Phil. Trans. R. Soc. A, 2007, 365(1858), 2203–2214. doi: 10.1098/rsta.2007.2002 [34] M. L. Dubreil-Jacotin, Sur la détermination rigoureuse des ondes permanentes périodiques d'ampleur finie, J. Math. Pures Appl., 1934, 13, 217–291. [35] F. Kogelbauer, On symmetric water waves with constant vorticity, J. Nonlinear Math. Phys., 2015, 22(4), 494–498. [36] F. Kogelbauer, Symmetric irrotational water waves are traveling waves, J. Differential Equations, 2015, 259(10), 5271–5275. doi: 10.1016/j.jde.2015.06.025 [37] F. Kogelbauer, On the symmetry of spatially periodic two-dimensional water waves, Discrete Contin. Dyn. Syst., 2016, 36(12), 7057–7061. doi: 10.3934/dcds.2016107 [38] D. Ionescu-Kruse and C. I. Martin, Periodic equatorial water flows from a Hamiltonian perspective, J. Differential Equations, 2017, 262(8), 4451–4474. doi: 10.1016/j.jde.2017.01.001 [39] D. Ionescu-Kruse and A.-V. Matioc, Small-amplitude equatorial water waves with constant vorticity: Dispersion relations and particle trajectories, Discrete Contin. Dyn. Syst., 2014, 34(8), 3045–3060. doi: 10.3934/dcds.2014.34.3045 [40] J. Li, Geometric properties and exact travelling wave solutions for the generalized Burger-Fisher equation and the Sharma-Tasso-Olver equation, J. Nonl. Mod. Anal., 2019, 1(1), 1–10. [41] X. Li, F. Meng and Z. Du, Traveling wave solutions of a fourth-order generalized dispersive and dissipative equation, J. Nonl. Mod. Anal., 2019, 1(3), 307–318. [42] A.-V. Matioc and B.-V. Matioc, Regularity and symmetry properties of rotational solitary water waves, J. Evol. Equ., 2012, 12(2), 481–494. doi: 10.1007/s00028-012-0141-7 [43] A.-V. Matioc and B.-V. Matioc, On the symmetry of periodic gravity water waves with vorticity, Differential Integral Equations, 2013, 26(1–2), 129–140. [44] B.-V. Matioc, A characterization of the symmetric steady water waves in terms of the underlying flow, Discrete Contin. Dyn. Syst., 2014, 34(8), 3125–3133. doi: 10.3934/dcds.2014.34.3125 [45] J. McCarney, Nonhydrostatic internal waves in the presence of mean currents and rotation, J. Math. Phys., 2014, 65(4), 10 pp. [46] B. Cushman-Roisin and J. M. Beckers, Introduction to Geophysical Fluid Dynamics: Physical and Numerical Aspects, Academic, Waltham, Mass., 2011. [47] G. Tulzer, On the symmetry of steady periodic water waves with stagnation points, Commun. Pure Appl. Anal., 2012, 11(4), 1577–1586. doi: 10.3934/cpaa.2012.11.1577 [48] S. Walsh, Some criteria for the symmetry of stratified water waves, Wave Motion, 2009, 46(6), 350–362. doi: 10.1016/j.wavemoti.2009.06.008 [49] L. Wang, Analyticity of rotational traveling capillary-gravity waves with critical layers, Nonlinear Anal., 2023, 227, 18 pp. [50] X. Wang and Y. Yang, On some recently derived exact solutions to the Euler equations, Appl. Anal., 2024, 103(5), 998–1007. doi: 10.1080/00036811.2023.2223201 [51] H. Wen and J. Huang, Traveling wave of three-species stochastic Lotka-Volterra competitive system, J. Nonl. Mod. Anal., 2024, 6(1), 32–55. [52] M. Wheeler, On stratified water waves with critical layers and Coriolis forces, Discrete Contin. Dyn. Syst., 2019, 39(8), 4747–4770. doi: 10.3934/dcds.2019193 [53] F. Xu, F. Li and Y. Zhang, The symmetry of steady stratified periodic gravity water waves, Monatsh. Math., 2024, 203(1), 247–266. -
-
Figures(2)
Export File
Citation
Yanjuan Yang, Jin Zhao. SYMMETRY OF ROTATIONAL EQUATORIAL INTERNAL WAVES[J]. Journal of Applied Analysis & Computation, 2025, 15(4): 2461-2473. doi: 10.11948/20240514
Format
Content
DownLoad:
-
Figure 1.
Symmetrization in the physical variables.
-
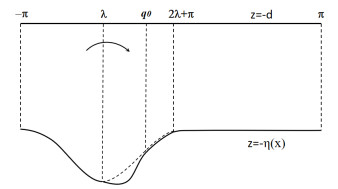
Figure 2.
Symmetrization in the
$ (q,p) $