| Citation: | D. Vijayaraghavan, S. Yugesh, Sunil Kumar. A STUDY ON FRACTIONAL LANE–EMDEN EQUATION OF ASTROPHYSICS AS THERMAL EXPLOSIONS USING CHEBYSHEV WAVELET METHOD[J]. Journal of Applied Analysis & Computation, 2025, 15(6): 3603-3628. doi: 10.11948/20240557 |
A STUDY ON FRACTIONAL LANE–EMDEN EQUATION OF ASTROPHYSICS AS THERMAL EXPLOSIONS USING CHEBYSHEV WAVELET METHOD
-
Abstract
Thermal explosions in astrophysical systems are crucial for understanding stellar evolution and dynamics. The fractional Lane–Emden equation is a key mathematical tool for modeling these explosions, providing insight into the thermodynamic processes within stellar interiors. Knowledge of such equations is significant because they quantify the temperature field and transport of energy within self-gravitating systems. A notable challenge in solving these equations arises from the singularity at $ x=0 $, which requires careful numerical handling. Standard analytical methods may not give exact solutions to fractional-order models, necessitating effective numerical solutions. In this paper, we use the second-kind Chebyshev wavelet approximation to solve the fractional Lane–Emden equation effectively. This method utilizes orthogonality and the wavelet operational matrices to convert the original problem into algebraic equations, significantly reducing the computational burden. Numerical experiments confirm that the presented technique is not only efficient and precise but also has the least computational cost compared to traditional numerical methods. Therefore, it makes it highly suitable for solving other complex fractional models in astrophysics.
-

-
References
[1] H. Adibi and A. M. Rismani, On using a modified Legendre-spectral method for solving singular IVPs of Lane–Emden type, Computers and Mathematics with Applications, 2010, 60(7), 2126–2130. doi: 10.1016/j.camwa.2010.07.056 [2] G. Adomian, R. Rach and N. T. Shawagfeh, On the analytic solution of the Lane–Emden equation, Foundations of Physics Letters, 1995, 8(2), 161–181. doi: 10.1007/BF02187585 [3] H. M. Ahmed, Numerical solutions for singular Lane–Emden equations using shifted Chebyshev polynomials of the first kind, Contemporary Mathematics, 2023, 4(1), 132–149. [4] A. El-Ajou, Z. Odibat, S. Momani and A. Alawneh, Construction of analytical solutions to fractional differential equations using homotopy analysis method, IAENG International Journal of Applied Mathematics, 2010, 40(2), 43–51. [5] A. Akgül, M. Inc, E. Karatas and D. Baleanu, Numerical solutions of fractional differential equations of Lane–Emden type by an accurate technique, Advances in Difference Equations, 2015, 220, 1–12. [6] E. K. Akgul, Solutions of the linear and nonlinear differential equations within the generalized fractional derivatives, Chaos, 2019, 29(2), 1–6. [7] S. S. Alzaid, P. K. Shaw and S. Kumar, A numerical study of fractional population growth and nuclear decay model, AIMS Mathematics, 2022, 7(6), 11417–11442. doi: 10.3934/math.2022637 [8] S. S. Alzaid, P. K. Shaw and S. Kumar, A study of Ralston's cubic convergence with the application of population growth model, AIMS Mathematics, 2022, 7(6), 11320–11344. doi: 10.3934/math.2022632 [9] E. Babolian and F. FattahZadeh, Numerical solution of differential equations by using Chebyshev wavelet operational matrix of integration, Applied Mathematics and Computation, 2007, 188(1), 417–426. doi: 10.1016/j.amc.2006.10.008 [10] A. H. Bhrawy and A. S. Alofi, A Jacobi–Gauss collocation method for solving nonlinear Lane–Emden type equations, Communications in Nonlinear Science and Numerical Simulation, 2012, 17(1), 62–70. doi: 10.1016/j.cnsns.2011.04.025 [11] A. H. Bhrawy, M. M. Tharwat and A. Yildirim, A new formula for fractional integrals of Chebyshev polynomials application for solving multi-term fractional differential equations, Applied Mathematical Modeling, 2013, 37(6), 4245–4252. doi: 10.1016/j.apm.2012.08.022 [12] J. -F. Cheng and Y. -M. Chu, Solution to the linear fractional differential equation using Adomian decomposition method, Mathematical Problems in Engineering, 2011. DOI: 10.1155/2011/587068. [13] C. K. Chui, An Introduction to Wavelets, Academic Press, 1992. [14] Daubechies, Ten Lectures of Wavelets, Springer-Verlag, 1992. [15] M. Dehghan and A. Saadatmandi, Chebyshev finite difference method for Fredholm integro-differential equation, International Journal of Computer Mathematics, 2008, 85(1), 123–130. doi: 10.1080/00207160701405436 [16] K. Diethelm, The Analysis of Fractional Differential Equations, Springer, 2010. [17] E. H. Doha, W. M. Abd-Elhameed and Y. H. Youssri, Second kind Chebyshev operational matrix algorithm for solving differential equations of Lane–Emden type, New Astronomy, 2013, 23–24, 113–117. [18] W. M. Abd-Elhameed, E. H. Doha and Y. H. Youssri, New spectral second kind Chebyshev wavelets algorithm for solving linear and nonlinear second-order differential equations involving singular and Bratu type equations, Abstract and Applied Analysis, 2013, 2013, 1–9. [19] V. Daftardar-Gejji and H. Jafari, Solving a multi-order fractional differential equation using Adomian decomposition, Applied Mathematics and Computation, 2007, 189(1), 541–548. doi: 10.1016/j.amc.2006.11.129 [20] R. Gupta and S. Kumar, Numerical simulation of variable order fractional differential equation of nonlinear Lane–Emden type appearing in astrophysics, International Journal of Nonlinear Sciences and Numerical Simulation, 2023, 24(3), 965–988. doi: 10.1515/ijnsns-2021-0092 [21] J. H. He, G. C. Wu and F. Austin, The variational iteration method which should be followed, Nonlinear Science Letters A, 2010, 1(1), 1–30. [22] C. Hunter, Series solutions for polytropes and the isothermal sphere, Monthly Notices of the Royal Astronomical Society, 2001, 328(3), 839–847. doi: 10.1046/j.1365-8711.2001.04914.x [23] R. W. Ibrahim, Existence of nonlinear Lane–Emden equation of fractional order, Miskolc Mathematical Notes, 2012, 13(1), 39–52. doi: 10.18514/MMN.2012.453 [24] F. İdiz, G. Tanoğlu and N. Aghazadeh, A numerical method based on Legendre wavelet and quasilinearization technique for fractional Lane–Emden type equations, Numerical Algorithms, 2023, 95(1), 132–149. [25] M. A. Iqbal, A. Ali and S. T. Mohyud-Din, Chebyshev wavelets method for fractional delay differential equations, International Journal of Modern Applied Physics, 2013, 4(1), 49–61. [26] H. Kaur, R. C. Mittal and V. Mishra, Haar wavelet approximate solutions for the generalized Lane–Emden equations arising in astrophysics, Computer Physics Communications, 2013, 184(9), 2169–2177. doi: 10.1016/j.cpc.2013.04.013 [27] A. M. M. Khodier and A. Y. Hassan, One-dimensional adaptive grid generation, International Journal of Mathematics and Mathematical Sciences, 1997, 20(3), 577–584. doi: 10.1155/S0161171297000781 [28] S. Kumar, A. Ahmadian, R. Kumar, D. Kumar, J. Singh, D. Baleanu and M. Salimi, An efficient numerical method for fractional SIR epidemic model of infectious disease by using Bernstein wavelets, Mathematics, 2020, 8(4), 1–22. [29] S. Kumar, R. Kumar, C. Cattani and B. Samet, Chaotic behaviour of fractional predator-prey dynamical system, Chaos, Solitons and Fractals, 2020, 135, 1–12. [30] S. Kumar, R. Kumar, M. S. Osman and B. Samet, A wavelet based numerical scheme for fractional order SEIR epidemic of measles by using Genocchi polynomials, Numerical Methods for Partial Differential Equations, 2020, 37(2), 1250–1268. [31] S. Kumar, R. Kumar, J. Singh, K. S. Nisar and D. Kumar, An efficient numerical scheme for fractional model of HIV-1 infection of CD4+ T-cells with the effect of antiviral drug therapy, Alexandria Engineering Journal, 2020, 59(4), 2053–2064. doi: 10.1016/j.aej.2019.12.046 [32] S. Kumar, P. K. Shaw, A. H. Abdel‐Aty and E. E. Mahmoud, A numerical study on fractional differential equation with population growth model, Numerical Methods for Partial Differential Equations, 2020, 40(1), 1–24. [33] Y. L. Li and N. Sun, Numerical solution of fractional differential equations using the generalized block pulse operational matrix, Computers and Mathematics with Applications, 2011, 62(3), 1046–1054. doi: 10.1016/j.camwa.2011.03.032 [34] Y. Li, N. Sun, B. Zheng, Q. Wang and Y. Zhang, Wavelet operational matrix method for solving the Riccati differential equation, Communications in Nonlinear Science and Numerical Simulation, 2014, 19(3), 483–493. doi: 10.1016/j.cnsns.2013.05.022 [35] X. Li, M. Xu and X. Jiang, Homotopy perturbation method to time-fractional diffusion equation with a moving boundary condition, Applied Mathematics and Computation, 2009, 208(2), 434–439. doi: 10.1016/j.amc.2008.12.023 [36] Y. L. Li and W. W. Zhao, Haar wavelet operational matrix of fractional order integration and its applications in solving the fractional order differential equations, Applied Mathematics and Computation, 2010, 216(8), 2276–2285. doi: 10.1016/j.amc.2010.03.063 [37] S. Mall and S. Chakraverty, A novel Chebyshev neural network approach for solving singular arbitrary order Lane–Emden equation arising in astrophysics, Network: Computation in Neural Systems, 2020, 31(1–4), 142–165. [38] H. R. Marasi, N. Sharifi and H. Piri, Modified differential transform method for singular Lane–Emden equations in integer and fractional order, TWMS Journal of Applied and Engineering Mathematics, 2015, 5(1), 124–131. [39] M. S. Mechee and N. Senu, Numerical study of fractional differential equations of Lane–Emden type by the least square method, International Journal of Differential Equations and Applications, 2012, 11(3), 157–168. [40] K. S. Miller and B. Ross, An Introduction to the Fractional Calculus and Fractional Differential Equations, Wiley, New York, 1993. [41] B. M. Mirza, Approximate analytical solutions of the Lane–Emden equation for a self-gravitating isothermal gas sphere, Monthly Notices of the Royal Astronomical Society, 2009, 395(4), 2288–2291. doi: 10.1111/j.1365-2966.2009.14697.x [42] A. Mohammadi, G. Ahmadnezhad and N. Aghazadeh, Chebyshev-quasilinearization method for solving fractional singular nonlinear Lane–Emden equations, Communications in Mathematics, 2022, 30(1), 201–228. [43] H. Mohammadi, S. Kumar, S. Rezapour and S. Etemad, A theoretical study of the Caputo–Fabrizio fractional modeling for hearing loss due to Mumps virus with optimal control, Chaos, Solitons and Fractals, 2021. DOI: 10.1016/j.chaos.2021.110668. [44] R. Yulita Molliq, M. S. M. Noorani and I. Hashim, Variational iteration method for fractional heat and wave-like equations, Nonlinear Analysis: Real World Applications, 2009, 10(3), 1854–1869. [45] S. Momani and Z. Odibat, Homotopy perturbation method for nonlinear partial differential equations of fractional order, Physics Letters A, 2007, 365(5–6), 345–350. [46] S. Momani and Z. Odibat, Numerical approach to differential equations of fractional order, Journal of Computational and Applied Mathematics, 2007, 201(3), 96–110. [47] E. Momoniat and C. Harley, Approximate implicit solution of a Lane–Emden equation, New Astronomy, 2006, 11(7), 520–526. [48] A. Kazemi Nasab, A. Kılıcman, Z. Pashazadeh Atabakan and S. Abbasbandy, Chebyshev wavelet finite difference method: A new approach for solving initial and boundary value problems of fractional order, Abstract and Applied Analysis, 2013, 2013, 1–15. [49] A. Kazemi Nasab, A. Kılıcman, Z. Pashazadeh Atabakan and W. J. Leong, A numerical approach for solving singular nonlinear Lane–Emden type equations arising in astrophysics, New Astronomy, 2015, 34, 178–186. [50] A. Kazemi Nasab, Z. Pashazadeh Atabakan, A. I. Ismail and R. W. Ibrahim, A numerical method for solving singular fractional Lane–Emden type equations, Journal of King Saud University–Science, 2018, 30(1), 120–130. [51] M. I. Nouh, Accelerated power series solution of polytropic and isothermal gas spheres, New Astronomy, 2004, 9(6), 467–473. [52] M. I. Nouh and E. A. Abdel-Salam, Approximate solution to the fractional Lane–Emden type equations, Iranian Journal of Science and Technology, Transactions A: Science, 2017, 42, 2199–2206. [53] Z. Odibat, S. Momani and V. S. Erturk, Generalized differential transform method: Application to differential equations of fractional order, Applied Mathematics and Computation, 2008, 197(2), 467–477. [54] R. K. Pandey, N. Kumar, A. Bhardwaj and G. Dutta, Solution of Lane–Emden type equations using Legendre operational matrix of differentiation, Applied Mathematics and Computation, 2012, 218(14), 7629–7637. [55] K. Parand, M. Dehghan, A. R. Rezaei and S. M. Ghaderi, An approximation algorithm for the solution of the nonlinear Lane–Emden type equations arising in astrophysics using Hermite functions collocation method, Computer Physics Communications, 2010, 181(6), 1096–1108. [56] K. Parand, M. Shahini and M. Dehghan, Rational Legendre pseudospectral approach for solving nonlinear differential equations of Lane–Emden type, Journal of Computational Physics, 2009, 228(23), 8830–8840. [57] I. Podlubny, An Introduction to Fractional Derivatives, Fractional Differential Equations, to Methods of their Solution and Some of their Applications, Academic Press, New York, 1999. [58] S. Saha Ray and R. K. Bera, An approximate solution of a nonlinear fractional differential equation by Adomian decomposition method, Applied Mathematics and Computation, 2005, 167(1), 561–571. [59] O. W. Richardson, The Emission of Electricity from Hot Bodies, Longmans Green and Co., London, 1921. [60] R. Saadeh, A. Burqan and A. El-Ajou, Reliable solutions to fractional Lane–Emden equations via Laplace transform and residual error function, Alexandria Engineering Journal, 2022, 61, 10551–10562. [61] U. Saeed, Haar Adomian method for the solution of fractional nonlinear Lane–Emden type equations arising in astrophysics, Taiwanese Journal of Mathematics, 2017, 21(5), 1175–1192. [62] P. K. Sahu and B. Mallick, Approximate solution of fractional order Lane–Emden type differential equation by orthonormal Bernoulli's polynomials, International Journal of Applied and Computational Mathematics, 2019. DOI: 10.1007/s40819-019-0677-0. [63] P. K. Sahu and R. S. Saha, Numerical solutions for Volterra integro-differential forms of Lane–Emden equations of first and second kind using Legendre multi wavelets, Electronic Journal of Differential Equations, 2015, 2015(28), 1–11. [64] Z. Seidov, Lane–Emden Equation: Perturbation Method, Astrophysics, 2004. DOI: 10.48550/arXiv.astro-ph/0402130. [65] B. Sharma, S. Kumar, M. K. Paswan and D. Mahato, Chebyshev operational matrix method for Lane–Emden Problem, Nonlinear Engineering, 2019, 8(1), 1–9. [66] P. K. Shaw, S. Kumar, S. Momani and S. Hadid, Dynamical analysis of fractional plant disease model with curative and preventive treatments, Chaos, Solitons & Fractals, 2022. DOI: 10.1016/j.chaos.2022.112705. [67] P. K. Shaw, S. Kumar, S. Momani and S. Hadid, Two new quadratic schemes for fractional differential equation with world population growth model, Progress in Fractional Differentiation and Applications, 2023, 9(4), 545–564. [68] N. T. Shawagfeh, Non perturbative approximate solution for Lane–Emden equation, Journal of Mathematical Physics, 1993, 34(9), 4364–4369. [69] S. C. Shiralashetti, A. B. Deshi and P. B. Mutalik Desai, Haar wavelet collocation method for the numerical solution of singular initial value problems, Ain Shams Engineering Journal, 2016, 7(2), 663–670. [70] R. Singh, H. Garg and V. Guleria, Haar wavelet collocation method for Lane–Emden equations with Dirichlet, Neumann and Neumann-Robin boundary conditions, Journal of Computational and Applied Mathematics, 2019, 346, 150–161. [71] Swati, M. Singh and K. Singh, An efficient technique based on higher order Haar wavelet method for Lane–Emden equations, Mathematics and Computers in Simulation, 2023, 206, 21–39. [72] P. Veeresha, D. G. Prakasha and S. Kumar, A fractional model for propagation of classical optical solitons by using nonsingular derivative, Mathematical Methods in the Applied Sciences, 2020. DOI: 10.1002/mma.6335. [73] D. F. Walnut, An Introduction to Wavelet Analysis, Springer Science and Business Media, 2002. [74] Y. Wang and L. Zhu, Solving nonlinear Volterra integro-differential equations of fractional order by using Euler wavelet method, Advances in Difference Equations, 2017. DOI: 10.1186/s13662-017-1085-6. [75] G. K. Watugala, Sumudu transform: A new integral transform to solve differential equations and control engineering problems, International Journal of Mathematical Education in Science and Technology, 1993, 24(1), 35–43. [76] A. Wazwaz, A new algorithm for solving differential equations of Lane–Emden type, Applied Mathematics and Computation, 2001, 118(3), 287–310. [77] A. -M. Wazwaz, Adomian decomposition method for a reliable treatment of the Emden-Fowler equation, Applied Mathematics and Computation, 2005, 161(2), 543–560. [78] A. -M. Wazwaz, Partial Differential Equations and Solitary Waves Theory, Nonlinear Physical Science, Higher Education Press, Beijing; Springer, Berlin, 2009. [79] A. M. Wazwaz, R. Rach and J. S. Duan, Adomian decomposition method for solving the Volterra integral form of the Lane–Emden equations with initial values and boundary conditions, Applied Mathematics and Computation, 2013, 219(10), 5004–5019. [80] G. Wu and E. W. M. Lee, Fractional variational iteration method and its application, Physics Letters A, 2010, 374(25), 2506–2509. [81] A. Yıldırım and T. Ozis, Solutions of singular IVPs of Lane–Emden type by homotopy perturbation method, Physics Letters A, 2007, 369(1–2), 70–76. [82] A. Yıldırım and T. Özış, Solutions of singular IVPs of Lane–Emden type by the variational iteration method, Nonlinear Analysis, 2009, 70(6), 2480–2484. [83] F. K. Yin, W. Y. Han and J. Q. Song, Modified Laplace decomposition method for Lane–Emden type differential equations, International Journal of Applied Physics and Mathematics, 2013, 3(2), 98–102. [84] S. A. Yousefi, Legendre wavelets method for solving differential equations of Lane–Emden type, Applied Mathematical Computation, 2006, 181(2), 1417–1422. [85] Y. H. Youssri, W. M. Abd-Elhameed and E. H. Doha, Ultraspherical wavelets method for solving Lane–Emden type equations, Romanian Journal of Physics, 2015, 60(9), 1298–1314. [86] F. Zhou and X. Xu, Numerical solution of the convection diffusion equations by the second kind Chebyshev wavelets, Applied Mathematics and Computation, 2014, 247, 353–367. [87] L. Zhu and Q. Fan, Solving fractional nonlinear Fredholm integro-differential equations by the second kind Chebyshev wavelet, Communications in Nonlinear Science and Numerical Simulation, 2012, 17(6), 2333–2341. -
-
-
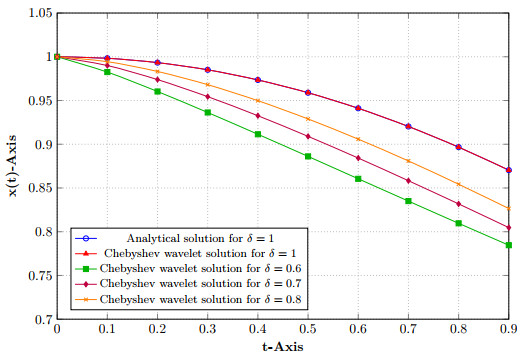
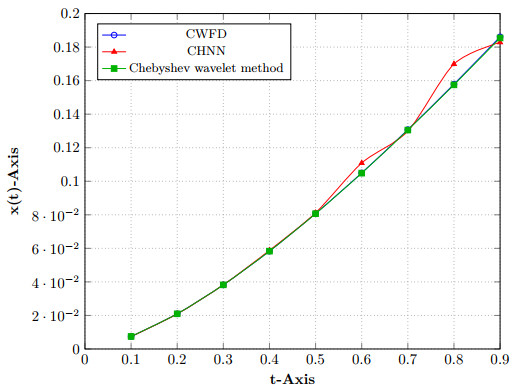
Figure 1.
Example 7.1.
-
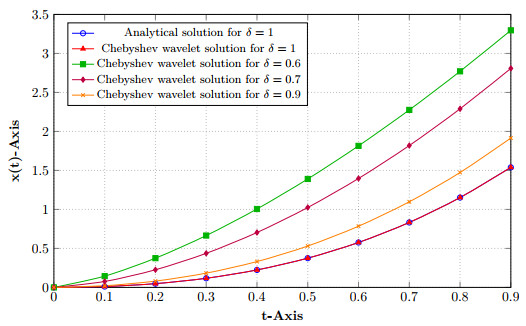
Figure 2.
Example 7.2.
-
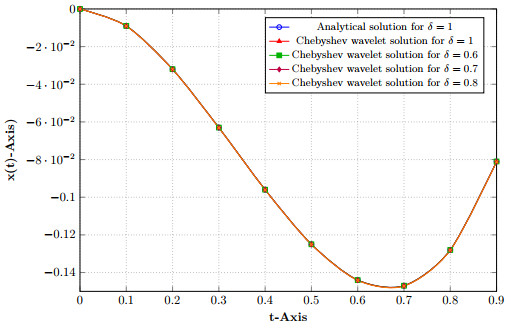
Figure 3.
Example 7.3.
-
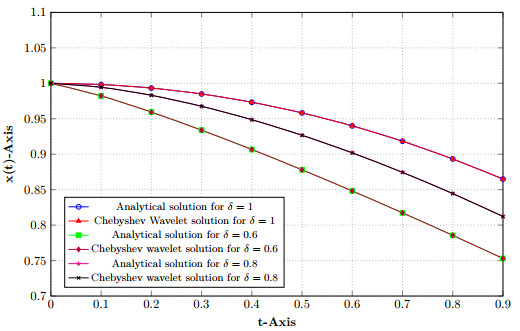
Figure 4.
Example 7.4.
-
Figure 5.
Example 7.5.




 DownLoad:
DownLoad: