| Citation: | Ayoub Louakar, Devaraj Vivek, Ahmed Kajouni, Khalid Hilal. EXISTENCE RESULTS OF HILFER FRACTIONAL STOCHASTIC PANTOGRAPH DIFFERENTIAL EQUATIONS WITH NON-INSTANTANEOUS IMPULSES VIA CONDENSING OPERATOR THEORY[J]. Journal of Applied Analysis & Computation, 2025, 15(6): 3629-3648. doi: 10.11948/20250001 |
EXISTENCE RESULTS OF HILFER FRACTIONAL STOCHASTIC PANTOGRAPH DIFFERENTIAL EQUATIONS WITH NON-INSTANTANEOUS IMPULSES VIA CONDENSING OPERATOR THEORY
-
Abstract
In this study, we establish the existence of mild solutions for fractional stochastic pantograph differential equations incorporating the Hilfer fractional derivative and non-instantaneous impulses. The analysis is conducted using tools from fractional calculus, semigroup theory, and stochastic analysis under appropriate conditions. Additionally, we employ condensing operator theory, the Hausdorff measure of noncompactness, and Sadovskii's fixed point theorem to derive our existence results. A detailed example, supported by graphical analysis, is presented to illustrate the practical applicability of the theoretical findings.
-

-
References
[1] T. Abdeljawad, K. Shah, M. S. Abdo and F. Jarad, An analytical study of fractional delay impulsive implicit systems with Mittag-Leffler law, Appl. Comput. Math., 2023, 22, 34–44. [2] A. S. Ahmed, Existence and uniqueness of mild solutions to neutral impulsive fractional stochastic delay differential equations driven by both Brownian motion and fractional Brownian motion, Differ. Equat. Appl., 2022, 14, 433–446. [3] H. M. Ahmed and J. R. Wang, Exact null controllability of Sobolev-Type Hilfer fractional stochastic differential equations with fractional Brownian motion and Poisson jumps, B. Iran. Math. Soc., 2018, 44, 673–690. doi: 10.1007/s41980-018-0043-8 [4] K. Balachandran, S. Kiruthika and J. J. Trujillo, Existence of solutions of nonlinear fractional pantograph equations, Acta Math. Sin., 2013, 33, 712–720. doi: 10.1016/S0252-9602(13)60032-6 [5] J. Banaś, Measures of noncompactness in the study of solutions of nonlinear differential and integral equations, Open Math., 2012, 10, 2003–2011. doi: 10.2478/s11533-012-0120-9 [6] T. Caraballo and M. A. Diop, Neutral stochastic delay partial functional integrodifferential equations driven by a fractional Brownian motion, Front. Math. China, 2013, 8, 745–760. doi: 10.1007/s11464-013-0300-3 [7] S. J. Daher, On a fixed point principle of Sadovskii, Nonlinear Analysis: Theory, Methods and Applications, 1978, 2, 643–645. [8] K. Deimling, Nonlinear Functional Analysis, Courier Corporation, 2010. [9] K. Diethelm and N. J. Ford, Analysis of fractional differential equations, J. Math. Anal. Appl., 2002, 265, 229–248. doi: 10.1006/jmaa.2000.7194 [10] P. Duan and Y. Ren, Solvability and stability for neutral stochastic integro-differential equations driven by fractional Brownian motion with impulses, Mediterr. J. Math., 2018, 15, 207. doi: 10.1007/s00009-018-1253-2 [11] K. M. Furati and M. D. Kassim, Existence and uniqueness for a problem involving Hilfer fractional derivative, Comput. Math. Appl., 2012, 64, 1616–1626. doi: 10.1016/j.camwa.2012.01.009 [12] G. R. Gautam and J. Dabas, Mild solutions for a class of neutral fractional functional differential equations with non-instantaneous impulses, Appl. Math. Comput., 2015, 259, 480–489. [13] H. Gu and J. J. Trujillo, Existence of mild solution for evolution equation with Hilfer fractional derivative, Appl. Math. Comput., 2015, 257, 344–354. [14] E. Hernández and D. ÓRegan, On a new class of abstract impulsive differential equations, Proc. Am. Math. Soc., 2013, 141, 1641–1649. [15] R. Hilfer, Applications of Fractional Calculus in Physics, World Scientific, Singapore, 1999. [16] F. Isaia, On a nonlinear integral equation without compactness, Acta Math. Univ. Comen., 2006, 75, 233–240. [17] M. B. Jeelani, K. Shah, H. Alrabaiah and A. S. Alnahdi, On a SEIR-type model of COVID-19 using piecewise and stochastic differential operators undertaking management strategies, AIMS Mathematics, 2023, 8, 27268–27290. doi: 10.3934/math.20231395 [18] J. L. Jensen, Sur les fonctions convexes et les inégalités entre les valeurs moyennes, Acta Mathematica, 1906, 30, 175–193. doi: 10.1007/BF02418571 [19] R. Kasinathan, R. Kasinathan and D. Chalishajar, Trajectory controllability of impulsive neutral stochastic functional integrodifferential equations driven by fBm with noncompact semigroup via Mönch fixed point, Qual. Theory Dyn. Syst., 2024, 23, 72. doi: 10.1007/s12346-023-00917-6 [20] H. Khalil, A. Zada, S. B. Moussa, I. L. Popa and A. Kallekh, Qualitative analysis of impulsive stochastic Hilfer fractional differential equation, Qual. Theory Dyn. Syst., 2024, 23, 1–21. doi: 10.1007/s12346-023-00858-0 [21] R. Kruse, Strong and Weak Approximation of Semilinear Stochastic Evolution Equations, Lecture Notes in Mathematics., Springer, Cham., 2014. [22] Y. Ma, H. Khalil, A. Zada and L. Popa, Existence theory and stability analysis of neutral $\psi$-Hilfer fractional stochastic differential system with fractional noises and non-instantaneous impulses, AIMS Math., 2024, 9, 8148–8173. doi: 10.3934/math.2024396 [23] A. B. Makhlouf and L. Mchiri, Some results on the study of Caputo–Hadamard fractional stochastic differential equations, Chaos Solitons Fractals, 2022, 155, 111757. doi: 10.1016/j.chaos.2021.111757 [24] A. B. Makhlouf, L. Mchiri and H. Rguigui, Ulam-Hyers stability of pantograph fractional stochastic differential equations, Math. Methods Appl. Sci., 2023, 46, 4134–4144. doi: 10.1002/mma.8745 [25] H. Mönch, Boundary value problems for nonlinear ordinary differential equations of second order in Banach spaces, Nonlinear Anal. Theory Methods Appl., 1980, 4, 985–999. doi: 10.1016/0362-546X(80)90010-3 [26] N. Mshary, H. M. Ahmed and A. S. Ghanem, Existence and controllability of nonlinear evolution equation involving Hilfer fractional derivative with noise and impulsive effect via Rosenblatt process and Poisson jumps, AIMS Math., 2024, 9, 9746–9769. doi: 10.3934/math.2024477 [27] K. S. Nisar, Efficient results on Hilfer pantograph model with nonlocal integral condition, Alex. Eng. J., 2023, 80, 342–347. doi: 10.1016/j.aej.2023.08.061 [28] I. Podlubny, Fractional Differential Equations, New York. Academic Press, 1999. [29] B. Radhakrishnan, T. Sathya and M. A. Alqudah, Existence results for nonlinear Hilfer pantograph fractional integro-differential equations, Qual. Theory Dyn. Syst., 2024, 23, 237. doi: 10.1007/s12346-024-01069-x [30] Y. Ren, X. Cheng and R. Sakthivel, Impulsive neutral stochastic functional integro-differential equations with infinite delay driven by fBm, Appl. Math. Comput., 2014, 247, 205–212. [31] S. Saravanakumar and P. Balasubramaniam, Non-instantaneous impulsive Hilfer fractional stochastic differential equations driven by fractional Brownian motion, Stoch. Anal. Appl., 2021, 39, 549–566. doi: 10.1080/07362994.2020.1815545 [32] K. Shah, T. Abdeljawad, B. Abdalla and M. S. Abualrub, Utilizing fixed point approach to investigate piecewise equations with non-singular type derivative, AIMS Mathematics, 2022, 7, 14614–14630. doi: 10.3934/math.2022804 [33] K. Shah, T. Abdeljawad and H. Alrabaiah, On coupled system of drug therapy via piecewise equations, Fractals, 2022, 30, 2240206. doi: 10.1142/S0218348X2240206X [34] K. Shah, H. Naz, T. Abdeljawad and B. Abdalla, Study of fractional order dynamical system of viral infection disease under piecewise derivative, CMES-Computer Modeling in Engineering and Sciences, 2023, 136, 921–941. doi: 10.32604/cmes.2023.025769 [35] J. Vanterler da C. Sousa, D. S. Oliveira and E. Capelas de Oliveira, A note on the mild solutions of Hilfer impulsive fractional differential equations, Chaos Solitons Fractals, 2021, 147, 110944. doi: 10.1016/j.chaos.2021.110944 [36] H. Tahir, A. Din, K. Shah, B. Abdalla and T. Abdeljawad, Advances in stochastic epidemic modeling: Tackling worm transmission in wireless sensor networks, Math. Comput. Model. Dyn. Syst., 2024, 30, 658–682. doi: 10.1080/13873954.2024.2396480 [37] Z. Tomovski, R. Hilfer and H. M. Srivastava, Fractional and operational calculus with generalized fractional derivative operators and Mittag-Leffler type functions, Integral Transforms Spec. Funct., 2010, 21, 797–814. doi: 10.1080/10652461003675737 [38] D. Vivek, E. Elsayed and K. Kangarajan, Existence results for hybrid stochastic differential equations involving $\psi$-Hilfer fractional derivative, Turk. J. Math. Comput. Sci., 2022, 14, 138–144. doi: 10.47000/tjmcs.987414 [39] A. Wongcharoen, S. K. Ntouyas and J. Tariboon, Nonlocal boundary value problems for Hilfer-type pantograph fractional differential equations and inclusions, Adv. Differ. Equ., 2020, 8, 1–21. [40] R. Ye, Existence of solutions for impulsive partial neutral functional differential equation with infinite delay, Nonlinear Anal. Theory Methods Appl., 2010, 73, 155–162. doi: 10.1016/j.na.2010.03.008 -
-
-
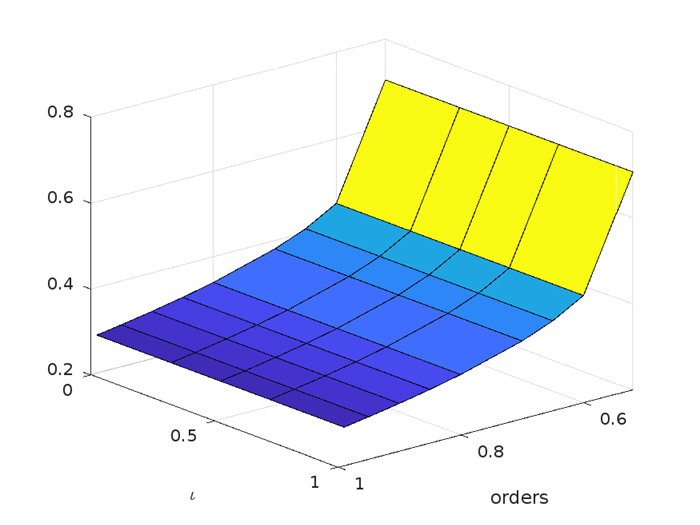
Figure 1.
Lipschitz constant with different values of orders.




 DownLoad:
DownLoad: