| Citation: | Juan Zhou, Kangkang Deng, Hongxia Wang, Zheng Peng. A NOVEL RIEMANNIAN CONJUGATE GRADIENT METHOD WITH ITERATION COMPLEXITY GUARANTEES[J]. Journal of Applied Analysis & Computation, 2026, 16(1): 209-228. doi: 10.11948/20240564 |
A NOVEL RIEMANNIAN CONJUGATE GRADIENT METHOD WITH ITERATION COMPLEXITY GUARANTEES
-
Abstract
Conjugate gradient methods are important first-order optimization algorithms both in Euclidean spaces and on Riemannian manifolds. However, while various types of Riemannian conjugate gradient methods have been studied, the iteration complexity analysis remains unknown. This paper proposes a novel Riemannian conjugate gradient method for nonconvex problems with an iteration complexity guarantee. In particular, we introduce a novel restart condition, leading to a function decrease at each iteration. Our method converges to an $ \epsilon $-stationary point with an iteration complexity of $ \mathcal{O}(\epsilon^{-2}) $. To the best of our knowledge, this is the first Riemannian conjugate gradient method with iteration complexity guarantees. Numerical experiments on Rayleigh-quotient and Brockett-cost-function minimization problems demonstrate the efficiency and practical applicability of the proposed method.
-

-
References
[1] P. -A. Absil, R. Mahony and R. Sepulchre, Optimization Algorithms on Matrix Manifolds, Princeton University Press, Princeton, NJ, 2008. [2] G. C. Bento, O. P. Ferreira and J. G. Melo, Iteration-complexity of gradient, subgradient and proximal point methods on Riemannian manifolds, Journal of Optimization Theory and Applications, 2017, 173(2), 548–562. [3] M. Bortoloti, T. A. Fernandes and O. P. Ferreira, An efficient damped Newton-type algorithm with globalization strategy on Riemannian manifolds, Journal of Computational and Applied Mathematics, 2022, 403, 113853. [4] N. Boumal, An Introduction to Optimization on Smooth Manifolds, Cambridge University Press, Cambridge, UK, 2023. [5] N. Boumal, P. -A. Absil and C. Cartis, Global rates of convergence for nonconvex optimization on manifolds, IMA Journal of Numerical Analysis, 2019, 39(1), 1–33. [6] N. Boumal, P. -A. Absil and C. Cartis, Global rates of convergence for nonconvex optimization on manifolds, IMA Journal of Numerical Analysis, 2019, 39(1), 1–33. [7] C. Cartis, P. R. Sampaio and P. L. Toint, Worst-case evaluation complexity of non-monotone gradient-related algorithms for unconstrained optimization, Optimization, 2015, 64(5), 1349–1361. [8] Y. Chen, K. Kuang and X. Yan, A modified PRP-type conjugate gradient algorithm with complexity analysis and its application to image restoration problems, Journal of Computational and Applied Mathematics, 2023, 427, 115105. [9] Y. -H. Dai and Y. -X. Yuan, A nonlinear conjugate gradient method with a strong global convergence property, SIAM Journal on Optimization, 1999, 10(1), 177–182. [10] K. Deng and J. Hu, Decentralized projected Riemannian gradient method for smooth optimization on compact submanifolds, arXiv preprint, 2023. arXiv: 2304.08241. [11] K. Deng, J. Hu and H. Wang, Decentralized douglas-rachford splitting methods for smooth optimization over compact submanifolds, arXiv preprint, 2023. arXiv: 2311.16399. [12] K. Deng and Z. Peng, A manifold inexact augmented Lagrangian method for nonsmooth optimization on Riemannian submanifolds in Euclidean space, IMA Journal of Numerical Analysis, 2023, 43(3), 1653–1684. [13] E. D. Dolan and J. J. Moré, Benchmarking optimization software with performance profiles, Mathematical Programming, 2002, 91, 201–213. [14] R. Fletcher and C. M. Reeves, Function minimization by conjugate gradients, The Computer Journal, 1964, 7(2), 149–154. [15] G. N. Grapiglia and E. W. Sachs, A generalized worst-case complexity analysis for non-monotone line searches, Numerical Algorithms, 2021, 87, 779–796. [16] L. Grippo, F. Lampariello and S. Lucidi, A nonmonotone line search technique for Newton's method, SIAM Journal on Numerical Analysis, 1986, 23(4), 707–716. [17] W. W. Hager and H. Zhang, A new conjugate gradient method with guaranteed descent and an efficient line search, SIAM Journal on Optimization, 2005, 16(1), 170–192. [18] M. R. Hestenes, E. Stiefel, et al., Methods of conjugate gradients for solving linear systems, Journal of Research of the National Bureau of Standards, 1952, 49(6), 409–436. [19] J. Hu, X. Liu, Z. -W. Wen and Y. -X. Yuan, A brief introduction to manifold optimization, Journal of the Operations Research Society of China, 2020, 8, 199–248. [20] W. Huang, P. -A. Absil and K. A. Gallivan, A Riemannian BFGS method without differentiated retraction for nonconvex optimization problems, SIAM Journal on Optimization, 2018, 28(1), 470–495. [21] R. Chan-Renous-Legoubin and C. W. Royer, A nonlinear conjugate gradient method with complexity guarantees and its application to nonconvex regression, EURO Journal on Computational Optimization, 2022, 10, 100044. [22] G. Montúfar and Y. G. Wang, Distributed learning via filtered hyperinterpolation on manifolds, Foundations of Computational Mathematics, 2022, 22(4), 1219–1271. [23] A. S. Nemirovsky and D. B. Yudin, Problem complexity and method efficiency in optimization, Journal of the Operational Research Society, 1984, 35(5). [24] Y. Nesterov, Introductory Lectures on Convex Optimization: A Basic Course, 87, Springer Science & Business Media, Berlin, Germany, 2013. [25] A. Neumaier, M. Kimiaei and B. Azmi, Globally linearly convergent nonlinear conjugate gradients without wolfe line search, Numerical Algorithms, 2024, 1–27. [26] J. Nocedal and S. J. Wright, Numerical Optimization, Springer, Berlin, 1999. [27] E. Polak and G. Ribiere, Note sur la convergence de méthodes de directions conjuguées, Revue Française D'informatique et de Recherche Opérationnelle. Série Rouge, 1969, 3(16), 35–43. [28] B. T. Polyak, The conjugate gradient method in extremal problems, USSR Computational Mathematics and Mathematical Physics, 1969, 9(4), 94–112. [29] M. J. D. Powell, Restart procedures for the conjugate gradient method, Mathematical Programming, 1977, 12, 241–254. [30] E. W. Sachs and S. M. Sachs, Nonmonotone line searches for optimization algorithms, Control and Cybernetics, 2011, 40(4), 1059–1075. [31] H. Sakai and H. Iiduka, Sufficient descent riemannian conjugate gradient methods, Journal of Optimization Theory and Applications, 2021, 190(1), 130–150. [32] H. Sakai, H. Sato and H. Iiduka, Global convergence of Hager–Zhang type Riemannian conjugate gradient method, Applied Mathematics and Computation, 2023, 441, 127685. [33] H. Sato, Riemannian Optimization and its Applications, SpringerBriefs in Electrical and Computer Engineering, Springer International Publishing, Cham, Switzerland, 2021. [34] H. Sato, Riemannian conjugate gradient methods: General framework and specific algorithms with convergence analyses, SIAM Journal on Optimization, 2022, 32(4), 2690–2717. [35] H. Sato, Riemannian optimization on unit sphere with p-norm and its applications, Computational Optimization and Applications, 2023, 1–39. [36] H. Sato and T. Iwai, A new, globally convergent riemannian conjugate gradient method, Optimization, 2015, 64(4), 1011–1031. [37] S. T. Smith, Optimization techniques on Riemannian manifolds, arXiv preprint, 2014. arXiv: 1407.5965. [38] G. -J. Song, X. -Z. Wang and M. K. Ng, Riemannian conjugate gradient descent method for fixed multi rank third-order tensor completion, Journal of Computational and Applied Mathematics, 2023, 421, 114866. [39] J. Townsend, N. Koep and S. Weichwald, Pymanopt: A python toolbox for optimization on manifolds using automatic differentiation, Journal of Machine Learning Research, 2016, 17(137), 1–5. [40] M. Yamada and H. Sato, Conjugate gradient methods for optimization problems on symplectic stiefel manifold, IEEE Control Systems Letters, 2023, 7, 2719–2724. [41] H. Zhang and W. W. Hager, A nonmonotone line search technique and its application to unconstrained optimization, SIAM Journal on Optimization, 2004, 14(4), 1043–1056. [42] H. Zhang and S. Sra, First-order methods for geodesically convex optimization, in Conference on Learning Theory, PMLR, 2016, 1617–1638. [43] Z. Zhao, X. -Q. Jin and T. -T. Yao, The Riemannian two-step perturbed Gauss–Newton method for least squares inverse eigenvalue problems, Journal of Computational and Applied Mathematics, 2022, 405, 113971. [44] X. Zhu and H. Sato, Riemannian conjugate gradient methods with inverse retraction, Computational Optimization and Applications, 2020, 77, 779–810. [45] X. Zhu and H. Sato, Cayley-transform-based gradient and conjugate gradient algorithms on Grassmann manifolds, Advances in Computational Mathematics, 2021, 47, 1–28. [46] X. Zhu and C. Shen, Practical gradient and conjugate gradient methods on flag manifolds, Computational Optimization and Applications, 2024, 1–34. -
-
-
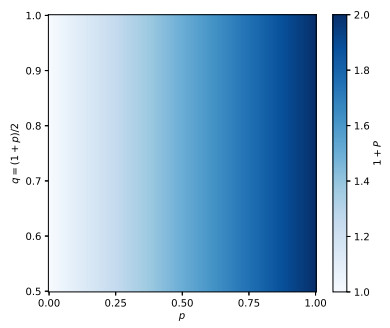
Figure 1.
Possible complexity values for different values of
$ p $ $ q $ $ 1+p-2 q=0 $ $ 1+p-q \geq 0 $ -
Figure 2.
Performance profiles of each algorithm versus the number of iterations (a) and the elapsed time (b) by Algorithm 1 using the FR, DY, PRP, and HZ methods from (2.6)
-
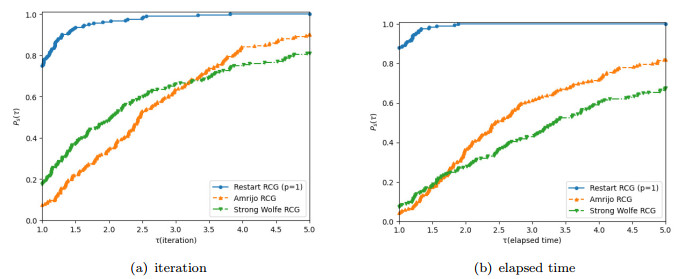
Figure 3.
Performance profiles of FR methods versus the number of iterations (a) and elapsed time (b) by Algorithm 1 using the modified restart condition, the Amrijo RCG and the Strong Wolfe RCG




 DownLoad:
DownLoad: