| Citation: | Han Xu, Xilin Fu. PERIODIC FLOWS IN SWITCHING DYNAMICAL SYSTEMS THROUGH DISCRETE IMPLICIT MAPPINGS[J]. Journal of Applied Analysis & Computation, 2026, 16(1): 229-245. doi: 10.11948/20240545 |
PERIODIC FLOWS IN SWITCHING DYNAMICAL SYSTEMS THROUGH DISCRETE IMPLICIT MAPPINGS
-
Abstract
In this paper, we investigate the periodic flow in a switching dynamical system through an implicit mapping method. By the given accuracy and the transport law, discrete implicit mappings at switching points are obtained and the corresponding interpolation points are achieved. Discrete implicit mappings at non-switching points are obtained by the discretization of differential equations of the switching system and the corresponding interpolation points are also determined. Then the periodic flow expressed by interpolation points in one period is determined. A two-order impulsive system with a pulse at a fixed time is presented as an example. The implicit mapping method may provide a plan for the periodic flows in discontinuous dynamical systems.
-
Keywords:
- Switching systems /
- implicit mappings /
- mapping structures /
- periodic flows
-

-
References
[1] L. Baymout and R. Benterk, Four limit cycles of three-dimensional discontinuous piecewise differential systems having a sphere as switching manifold, Int. J. Bifurcat. Chaos, 2024, 34(03), 2450030. [2] M. S. Branicky, Analyziny continuous switching systems: Theory and example, in Proc. Amer. Contr. Conf., 1994, 3110–3114. [3] M. S. Branicky, Multiple Lyapunov functions and other analysis tools for switched and hybried systems, IEEE Trans. Automat. Contr., 1998, 43(4), 475–482. [4] C. Guo and A. C. J. Luo, Symmetric and asymmetric periodic motions of a nonlinear oscillotor with a tuned damper inerter, Eur. Phys. J. Spec. Top., 2021, 230, 3533–3549. [5] S. Guo and A. C. J. Luo, Period-1 to period-4 motions in a 5D Lorenz system, Int. J. Bifurcat. Chaos, 2024, 34(05), 2450065. [6] Y. Guo and A. C. J. Luo, On complex periodic motions and bifurcations in a periodically forced, damped, hardening Duffing oscillator, Chaos Soliton Fract., 2015, 81, 378–399. [7] Y. Guo and A. C. J. Luo, Period-3 motions to chaos in a periodically forced nonlinear-spring pendulum, Chaos, 2022, 32, 103129. [8] T. Koeppen, T. Kuepper and O. Makarenkov, Existence and stability of limit cycles in Control of anti-lock braking systems with two boundaries via perturbation theory, Internat. J. Control, 2017, 90, 974–989. [9] W. L. De Koning, Digital optimal reduced-order control of pulse-width-modulated switched linear systems, Automatica, 2003, 39(11), 1997–2003. [10] L. Li and A. C. J. Luo, On periodic solutions of a second-order time-delayed discontinuous dynamical system, Chaos Soliton. Fract., 2018, 114, 216–229. [11] Y. Liu, S. Yin, L. Zhang, X. Yin and H. Yan, Improved results on asymptotic stabilization for stochastic nonlinear time-delay systems with application to a chemical reactor system, IEEE T. Syst. Man CY-S., 2017, 47(1), 195–204. [12] J. Llibre, R. Oliveira and C. B. Rodrigues, On the periodic solutions of the Michelson continuous and discontinuous piecewise linear differential system, Comput. Appl. Math., 2018, 37, 1550–1561. [13] K. A. Loparo, J. T. Aslanis and O. Hajek, Analysis of switched linear systems in the plane, part 2: Global behavior of trajectories, controllability and attainability, J. Optimiz. Theory. App., 1987, 52(3), 395–427. [14] K. A. Loparo, J. T. Aslants and O. Hajek, Analysis of switched linear systems in the plane, part 1: Local behavior of trajectories and local cycle geometry, J. Optimiz. Theory. APP., 1987, 52(3), 365–394. [15] A. C. J. Luo, Discrete and Switching Dynamical Systems, Higher Education Press, Beijing, 2012. [16] A. C. J. Luo, Periodic flows to chaos based on discrete implicit mappings of continuous nonlinear systems, Int. Bifuroat. Chaos, 2015, 25(3), 1550044. [17] A. C. J. Luo and S. Xing, Symmetric and asymmetric period-1 motions in a periodically fored, time-delayed, hardening Duffing oscillator, Nonlinear Dyn., 2016, 85(2), 1141–1166. [18] A. C. J. Luo and S. Xing, Bifurcation trees of period-3 motions to chaos in a time-delayed Duffing oscillator, Nonlinear Dyn., 2017, 88(4), 2831–2862. [19] A. C. J. Luo and Y. Zhu, Periodic motions with impact chatters in an impact Duffing oscillator, Chaos, 2024, 34, 053124. [20] O. Makarenkov, Bifurcation of limit cycles from a switched equilibrium in planar switched systems, J. Franklin. I, 2019. [21] M. E. M. Meza, A. Bhaya, E. Kaszkurewicz and M. I. S. Costa, On-off policy and hysteresis on-off policy control of the herbivore-vegetation dynamics in a semi-arid grazing system, Ecol. Eng., 2006, 28, 114–123. [22] Y. Niu, D. W. C. Ho and J. Lam, Robust integral sliding mode control for uncertain stochastic systems with time-varying delay, Automatica, 2005, 41(5), 873–880. [23] P. Peleties and R. A. Decarlo, Asymptotic Stability of m-Switched Systems using Lyapunov-Like Functions, Proceeding of 31st IEEE Conference On Decision and Control, Tucson, AZ, USA, 1992. [24] A. V. Savkin and A. S. Matveev, Existence and stability of periodic trajectories in switched server systems, Automatica, 2000, 36, 775–779. [25] A. Schild, J. Lunze, J. Krupar and W. Schwarz, Design of generalized hysteresis controllers for DC-DC switching power converters, IEEE Trans. Power Electron., 2009, 24, 138–146. [26] Y. Shang, Resilient consensus of switched multi-agent systems, Syst. Control. Lett., 2018, 122, 12–18. [27] A G. Tanaka, K. Tsumoto, S. Tsuji and K. Aihara, Bifurcation analysis on a hybrid system model of intermittent hormonal therapy for prostate cancer, Phys. D., 2008, 237, 2616–2627. [28] P. P. Varaiya, Smart cars on smart roads: Problem of control, IEEE T. Automat. Cont., 1993, 8(2), 195–207. [29] E. Hernandez-Vargas, P. Conlaneri and R. Middleton, Discrete-time control for switched positive systems with application to mitigating viral esape, Int. J. Robust Nonlin., 2011, 21(10), 1093–1111. [30] X. Wang and L. Guo, Limit cycles in a switching Liénard system, Discrete Cont. Dyn. -B, 2023, 28(02), 1503–1512. [31] S. Xing and A. C. J. Luo, Period-1 motions to twin spiral homoclinic orbits in the Rossler system, J. Comput. Nonlin. Dyn., 2023, 18(08), 081008. [32] Y. Xu, Z. Chen and A. C. J. Luo, On bifurcation trees of period-1 to period-2 motions in a nonlinear Jeffcott rotor system, Int. J. Mech. SCI., 2019, 160, 429–500. [33] Y. Xu and A. C. J. Luo, Frequency-amplitude characteristic of periodic motions in a periodically forced Van der Pol oscillator, Eur. Phys. Special Topics, 2019, 228, 1839–1854. [34] Y. Xu and A. C. J. Luo, Indepent period-2 motions to chaos in a Van der Pol-Duffing oscillator, Int. J. Bifurca. Chaos, 2020, 30(15), 2030045. [35] X. Yang and G. Chen, Limit cycles and chaotic invariant sets in autonomous hybrid planar systems, Nonlinear Anal. -Hybri., 2008, 2, 952–957. [36] C. Zhang, Q. Tang and Z. Wang, Grazing and symmetry-breaking bifurcations induced oscillations in a switched system composed of Duffing and van der Pol oscillators, Mathematics, 2022, 10(05), 772. [37] X. Zhang, J. Zhou, C. Zhang and Q. Bi, Analysis of dynamical behaviors in a nonlinear switching circuit system, Acta Phys. Sin., 2013, 62, 240505. [38] S. Zheng and X. Fu, Periodic motion of the Van der Pol equation with impulsive effect, Int. J. Bifurcat. Chaos, 2015, 25(9), 1550119. [39] Y. Zhou, H. Hu, Y. Lin, S. Lin and Z. Ding, A distributed approach to robust control of multi-robot systems, Auctomatica, 2018, 98, 1–13. -
-
-
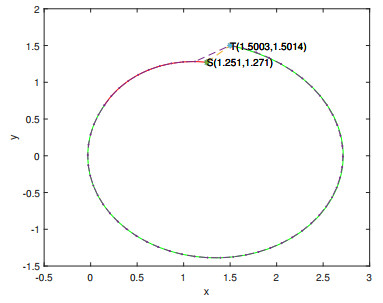
Figure 1.
The red curve crossing the point
$ S(1.251,1.271) $ $ [0,1] $ $ x(1)=1.251 $ $ y(1)=1.271; $ $ T(1.5012,1.5) $ $ x(1^{+})=1.5012 $ $ y(1^{+})=1.5 $ $ (1,6] $ -
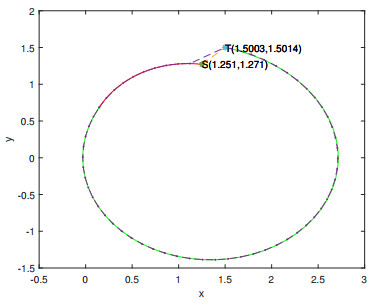
Figure 2.
Blue dots connecting with short lines depict the approximate periodic solution of Eq. (3.1) on the interval [0, 6].
-
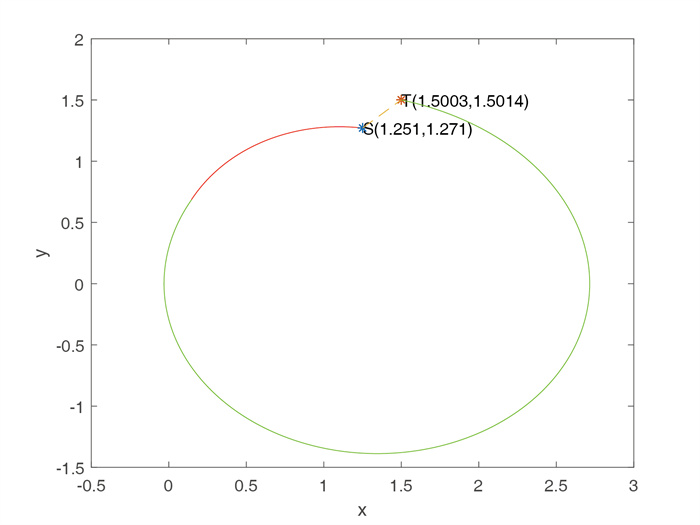
Figure 3.
Overlap of the approximate periodic solution of Eq. (3.1) and the analytical solution of Eq. (3.1).




 DownLoad:
DownLoad: