| Citation: | Di Yu, Xue Yang. USING HOMOTOPY MULTI-HIERARCHICAL ENCODER REPRESENTATION FROM TRANSFORMERS (HMHERT) FOR TIME SERIES CHAOS CLASSIFICATION[J]. Journal of Applied Analysis & Computation, 2026, 16(1): 246-269. doi: 10.11948/20250101 |
USING HOMOTOPY MULTI-HIERARCHICAL ENCODER REPRESENTATION FROM TRANSFORMERS (HMHERT) FOR TIME SERIES CHAOS CLASSIFICATION
-
Abstract
The Transformer architecture, renowned for its exceptional capacity in processing long-sequence data, inspires our framework that leverages its self-attention mechanism to classify time series through relational analysis between sequence elements. In this article, we propose a Homotopy Multi-Hierarchical Encoder Representation from Transformers (HMHERT), for chaotic/non-chaotic sequence classification. Empirical investigations into the linear combination coefficients of multi-head attention reveal that constrained homotopy coefficients significantly enhance model performance, with homotopy constrained configurations outperforming their unconstrained coefficient counterparts. Through systematic comparative analysis of Confusion Matrix, classification accuracy, F1-scores, and Matthews Correlation Coefficient (MCC), HMHERT exhibits significantly enhanced generalization performance, outperforming conventional models including Time-Delayed Reservoir Computing (RC), Fully Connected Neural Network (FCNN), Long Short Term Memory (LSTM), and Convolutional Neural Network (CNN) by 0.5097-0.9204 across MCC metrics. Furthermore, compared to the baseline Transformer encoder architecture, HMHERT achieves performance improvement, demonstrating the critical role of our proposed architectural modifications in chaotic pattern recognition.
-
Keywords:
- Chaotic classification /
- homotopy /
- multi-hierarchical /
- Transformer
-

-
References
[1] S. J. Anagnostopoulos, J. D. Toscano, N. Stergiopulos and G. E. Karniadakis, Residual-based attention in physics-informed neural networks. Computer Methods in Applied Mechanics and Engineering, 2024, 421: 116805. [2] A. Balestrino, A. Caiti and E. Crisostomi, Generalised entropy of curves for the analysis and classification of dynamical systems. Entropy, 2009, 11(2): 249-270. [3] N. Boullé, V. Dallas, Y. Nakatsukasa and D. Samaddar, Classification of chaotic time series with deep learning. Physica D: Nonlinear Phenomena, 2020, 403: 132261. [4] J. S. Cánovas, Topological sequence entropy of interval maps. Nonlinearity, 2003, 17(1): 49. [5] T. L. Carroll, Using reservoir computers to distinguish chaotic signals. Physical Review E, 2018, 98(5): 052209. [6] C. F. R. Chen, Q. Fan and R. Panda, Crossvit: Cross-attention multi-scale vision transformer for image classification. in Proceedings of the IEEE/CVF International Conference on Computer Vision, 2021, 357-366. [7] W. Chen and K. Shi, Multi-scale attention convolutional neural network for time series classification. Neural Networks, 2021, 136: 126-140. [8] Z. Cui, Q. Li, Z. Cao and N. Liu, Dense attention pyramid networks for multi-scale ship detection in sar images. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(11): 8983-8997. [9] J. Devlin, Bert: Pre-training of deep bidirectional transformers for language understanding. arXiv preprint, 2018. arXiv: 1810.04805. [10] H. Fan, B. Xiong, K. Mangalam, et al., Multiscale vision transformers. in Proceedings of the IEEE/CVF International Conference on Computer Vision, 2021, 6824-6835. [11] B. Feng and X. Zhou, Energy-informed graph transformer model for solid mechanical analyses. Communications in Nonlinear Science and Numerical Simulation, 2024, 108103. [12] N. Geneva and N. Zabaras, Transformers for modeling physical systems. Neural Networks, 2022, 146: 272-289. [13] D. Han, T. Ye, Y. Han, et al., Agent attention: On the integration of softmax and linear attention, in European Conference on Computer Vision. Springer, 2024, 124-140. [14] J. Hao and W. Zhu, Architecture self-attention mechanism: Nonlinear optimization for neural architecture search. J. Nonlinear Var. Anal, 2021, 5: 119-140. [15] A. Hemmasian and A. B. Farimani, Multi-scale time-stepping of partial differential equations with transformers. Computer Methods in Applied Mechanics and Engineering, 2024, 426: 116983. [16] Y. Li and Y. Li, A homotopy gated recurrent unit for predicting high dimensional hyperchaos. Communications in Nonlinear Science and Numerical Simulation, 2022, 115: 106716. [17] Y. Li and Y. Li, Predicting chaotic time series and replicating chaotic attractors based on two novel echo state network models. Neurocomputing, 2022, 491: 321-332. [18] D. W. Liedji, J. H. Talla Mbé and G. Kenné, Chaos recognition using a single nonlinear node delay-based reservoir computer. The European Physical Journal B, 2022, 95(1): 18. [19] D. Wenkack Liedji, J. H. Talla Mbé and G. Kenne, Classification of hyperchaotic, chaotic, and regular signals using single nonlinear node delay-based reservoir computers. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2022, 32(12). [20] B. Lim, S. Ö. Arık, N. Loeff and T. Temporal fusion transformers for interpretable multi-horizon time series forecasting. International Journal of Forecasting, 2021, 37(4): 1748-1764. [21] Z. Liu, Y. Lin, Y. Cao, et al., Swin transformer: Hierarchical vision transformer using shifted windows. in Proceedings of the IEEE/CVF International Conference on Computer Vision, 2021, 10012-10022. [22] E. N. Lorenz, Deterministic nonperiodic flow. Journal of Atmospheric Sciences, 1963, 20(2): 130-141. [23] H. Miao, W. Zhu, Y. Dan and N. Yu, Chaotic time series prediction based on multi-scale attention in a multi-agent environment, Chaos. Solitons & Fractals, 2024, 183: 114875. [24] S. Mukhopadhyay and S. Banerjee, Learning dynamical systems in noise using convolutional neural networks. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2020, 30(10). [25] Y. Pan, T. Yao, Y. Li and T. Mei, X-linear attention networks for image captioning. in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2020, 10971-10980. [26] A. Radford, Improving language understanding by generative pre-training, 2018. [27] A. Sinha and J. Dolz, Multi-scale self-guided attention for medical image segmentation. IEEE Journal of Biomedical and Health Informatics, 2020, 25(1): 121-130. [28] J. Su, H. Li, R. Wang, et al., A hybrid dual-branch model with recurrence plots and transposed transformer for stock trend prediction. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2025, 35(1). [29] S. Sun, W. Ren, X. Gao, et al., Restoring images in adverse weather conditions via histogram transformer, in European Conference on Computer Vision. Springer, 2024, 111-129. [30] A. Szczęsna, D. Augustyn, K. Harężlak, et al., Datasets for learning of unknown characteristics of dynamical systems. Scientific Data, 2023, 10(1): 79. [31] A. Vaswani, N. Shazeer, N. Parmar, et al., Attention is All You Need. Advances in Neural Information Processing Systems, 2017. [32] Y. Xiong, W. Yang, H. Liao, et al., Soft variable selection combining partial least squares and attention mechanism for multivariable calibration. Chemometrics and Intelligent Laboratory Systems, 2022, 223: 104532. [33] S. Yun and Y. Ro, Shvit: Single-head vision transformer with memory efficient macro design. in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2024, 5756-5767. [34] A. Zeng, M. Chen, L. Zhang and Q. Xu, Are transformers effective for time series forecasting?. in Proceedings of the AAAI Conference on Artificial Intelligence, 2023, 37: 11121-11128. [35] C. Zhao, J. Ye, Z. Zhu and Y. Huang, Flrnn-fga: Fractional-order lipschitz recurrent neural network with frequency-domain gated attention mechanism for time series forecasting. Fractal and Fractional, 2024, 8(7): 433. [36] L. Zhornyak, M. A. Hsieh and E. Forgoston, Inferring bifurcation diagrams with transformers. Chaos: An Interdisciplinary Journal of Nonlinear Science, 2024, 34(5). [37] H. Zhou, S. Zhang, J. Peng, et al., Informer: Beyond efficient transformer for long sequence time-series forecasting. in Proceedings of the AAAI Conference on Artificial Intelligence, 2021, 35: 11106-11115. [38] L. Zhu, X. Wang, Z. Ke, et al., Biformer: Vision transformer with bi-level routing attention. in Proceedings of the IEEE/CVF Conference on Computer Vision and Pattern Recognition, 2023, 10323-10333. -
-
-
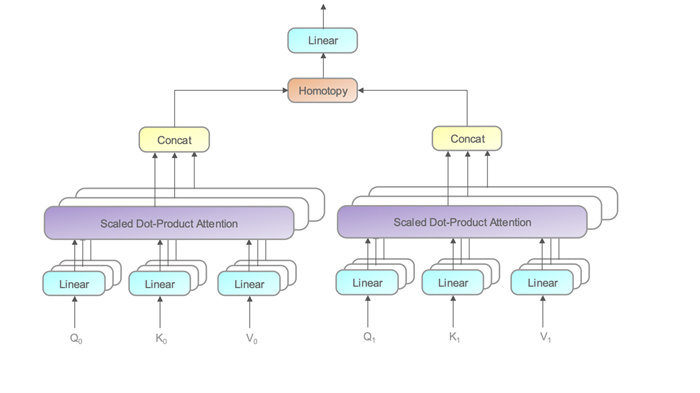
Figure 1.
Homotopy multi-hierarchical multi-head attention
-
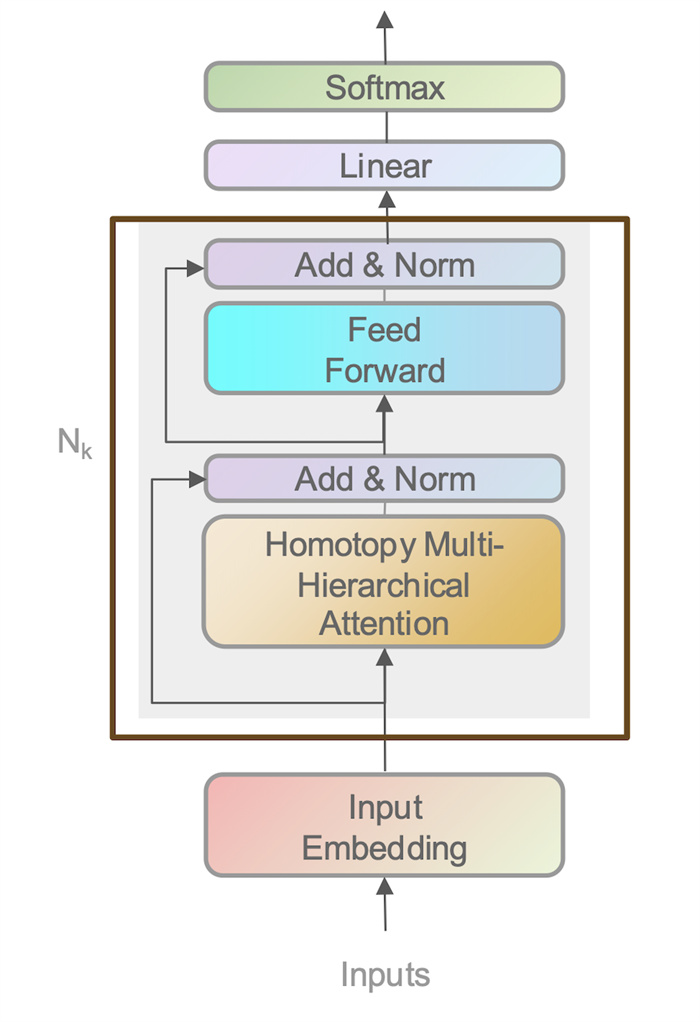
Figure 2.
HMHERT-model architecture
-
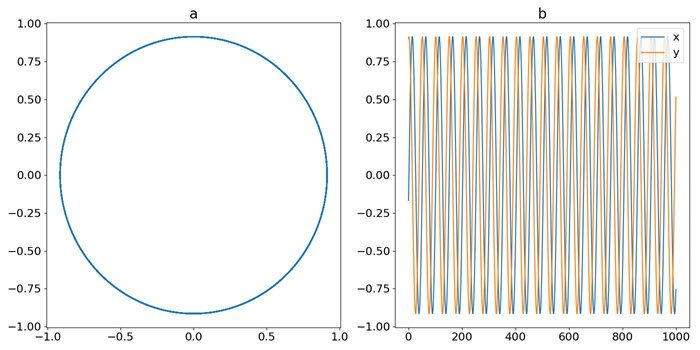
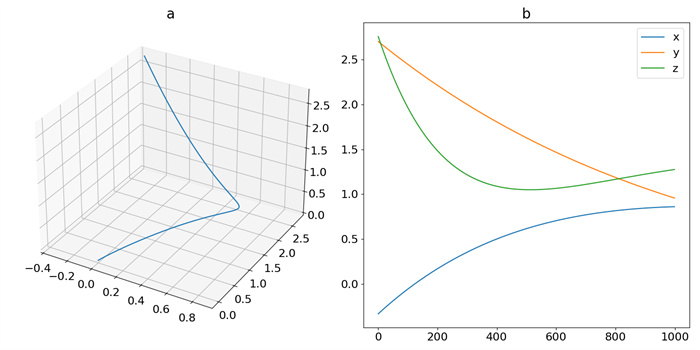
Figure 3.
Trajectory of OSC: (a) phase-space plot, (b) time-domain plot
-
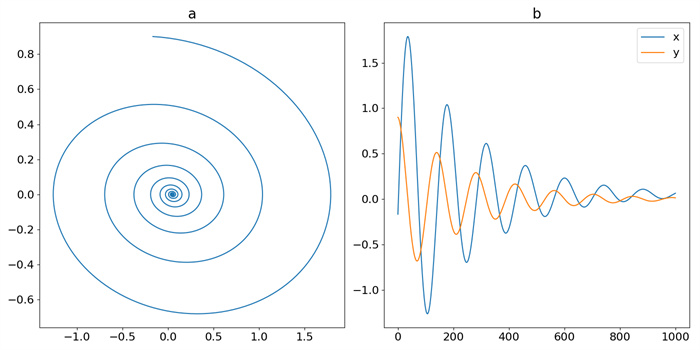
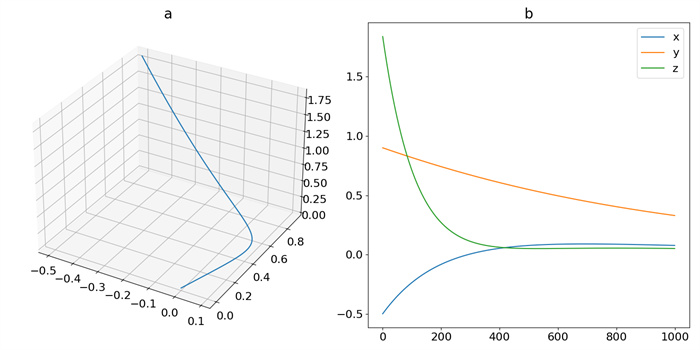
Figure 4.
Trajectory of DOSC: (a) phase-space plot, (b) time-domain plot
-
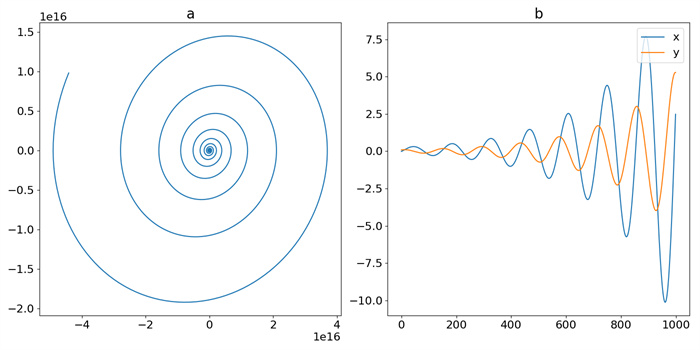
Figure 5.
Trajectory of IOSC: (a) phase-space plot, (b) time-domain plot
-
Figure 6.
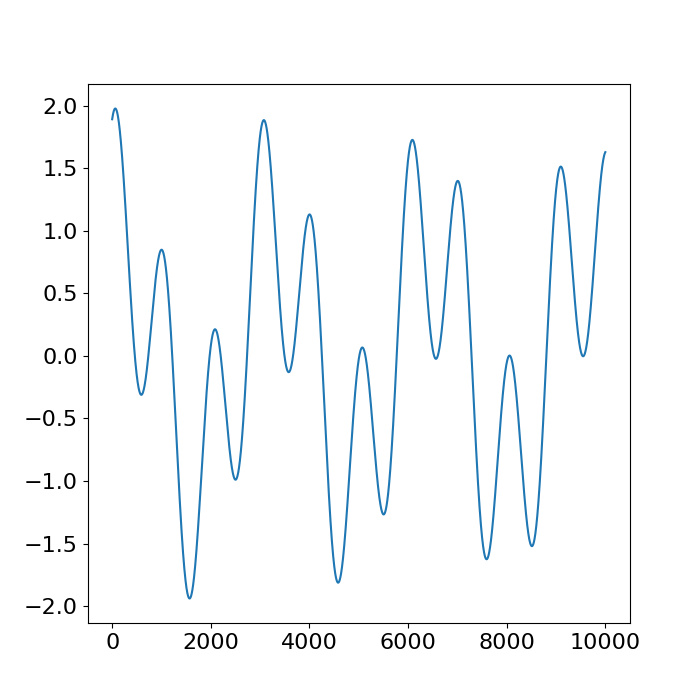
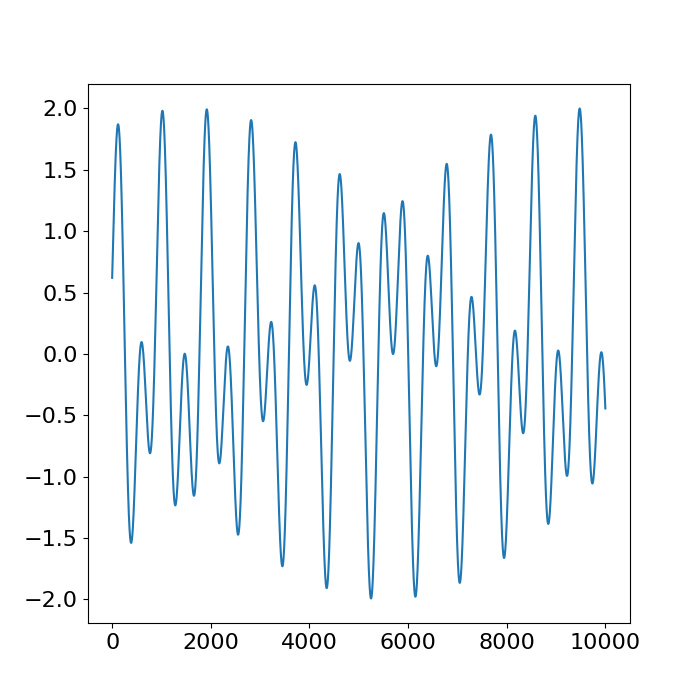
Trajectory of QPS_1: Time-domain plot
-
Figure 7.
Trajectory of QPS_2: Time-domain plot
-
Figure 8.
Trajectory of DS_1: (a) phase-space plot, (b) time-domain plot
-
Figure 9.
Trajectory of DS_2: (a) phase-space plot, (b) time-domain plot
-
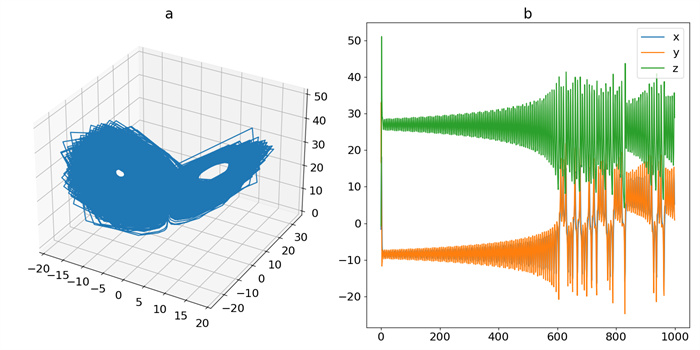
Figure 10.
Trajectory of CHA_1: (a) phase-space plot, (b) time-domain plot
-
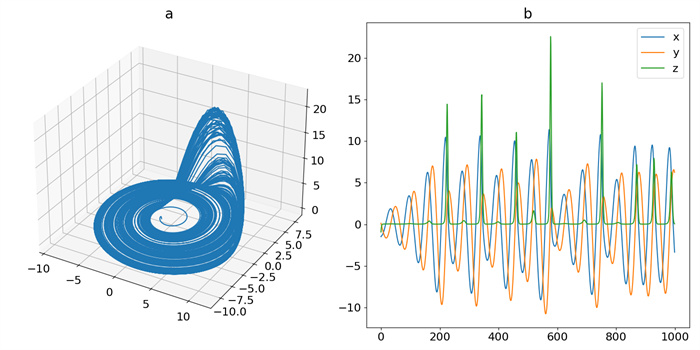
Figure 11.
Trajectory of CHA_2: (a) phase-space plot, (b) time-domain plot
-
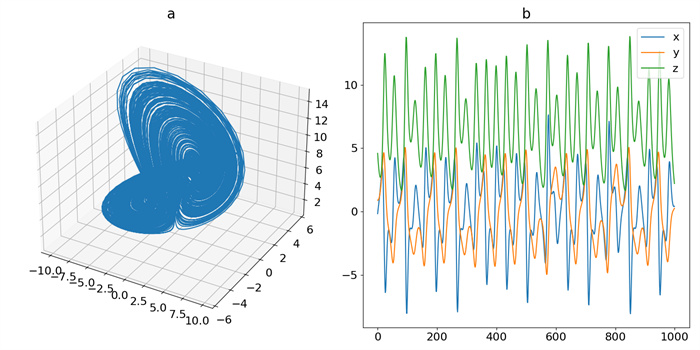
Figure 12.
Trajectory of CHA_3: (a) phase-space plot, (b) time-domain plot
-
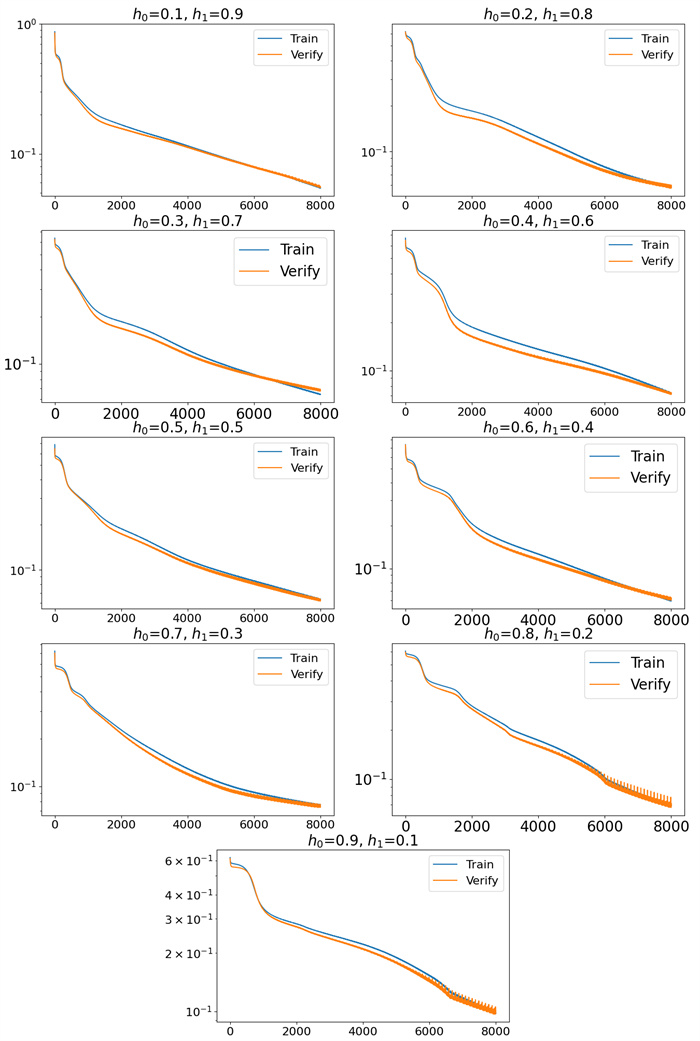
Figure 13.
The training loss function and validation loss function results of the HMHERT's multi-hierarchical multi-head attention mechanism under different homotopy coefficients are presented. The x-axis represents the training epochs, while the y-axis denotes the value of the loss function. The y-axis is plotted on a logarithmic scale
-
Figure 14.
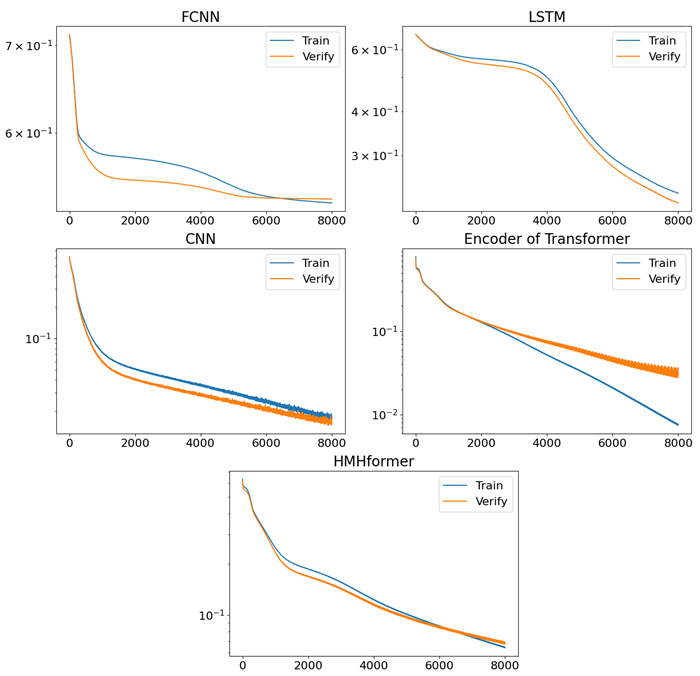
The training loss function and validation loss function results of different neural networks are presented (Time-Delayed RC is different from other neural network training methods, so there is no loss function diagram). The x-axis represents the training epochs, while the y-axis denotes the value of the loss function. The y-axis is plotted on a logarithmic scale
-
Figure 15.
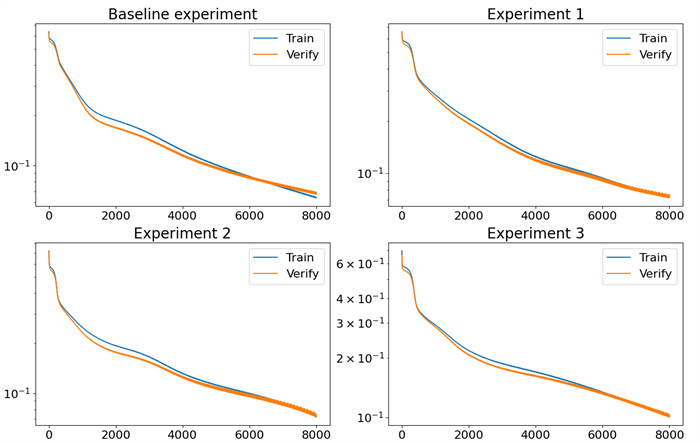
The results of the training and validation loss functions for the HMHERT under different training methods are presented. Additionally, the training and validation loss function results when the multi-hierarchical multi-head attention mechanism is unrestricted are also provided. The x-axis represents the training epochs, while the y-axis denotes the value of the loss function. The y-axis is plotted on a logarithmic scale




 DownLoad:
DownLoad: