| Citation: | Qian Gao, Bao Shi, Xiaodong Zhang. STABILIZATION OF A PARABOLIC PDE SANDWICHED BY TWO NONLINEAR ODES[J]. Journal of Applied Analysis & Computation, 2026, 16(1): 270-295. doi: 10.11948/20250106 |
STABILIZATION OF A PARABOLIC PDE SANDWICHED BY TWO NONLINEAR ODES
-
Abstract
This paper is devoted to the stabilization of a class of nonlinear parabolic ODE-PDE-ODE systems constituting by a parabolic equation sandwiched by two nonlinear ODEs. Different from the related literature where both the two ODE subsystems are linear time invariant (LTI) or only the ODE subsystem proximal to the control input is nonlinear but that distal to the input is LTI, serious nonlinearities are contained in the system under investigation since both the two ODE subsystems (no matter proximal or distal to the input) are all nonlinear which lead to the incapability of the control schemes on this topic. To solve the control problem, a novel control framework is established by smartly combining infinite-dimensional backstepping method with the the finite-dimensional one. Specifically, three steps of backstepping transformations are subsequently introduced for the system, which include two finite-dimensional ones respectively for the distal and proximal ODE subsystems and an infinite-dimensional one for the PDE subsystem. Then, a new target system is obtained under the backstepping transformations while a state-feedback controller is explicitly designed. Finally, by recursive analysis from the target system, desirable stability of the resulting closed-loop system is obtained, i.e., all the states of the resulting closed-loop system are bounded and converge to zero ultimately. A simulation example is provided to validate the effectiveness of the proposed theoretical results.
-
Keywords:
- ODE-PDE-ODE systems /
- nonlinearity /
- backstepping /
- stabilization /
- distributed parameter systems
-

-
References
[1] H. Anfinsen and O. M. Aamo, Stabilization of a linear hyperbolic PDE with actuator and sensor dynamics, Automatica, 2018, 95, 104–111. doi: 10.1016/j.automatica.2018.05.019 [2] B. P. Delphine and M. Krstić, Delay-adaptive predictor feedback for systems with unknown long actuator delay, IEEE Transactions on Automatic Control, 2010, 55(9), 2106–2112. doi: 10.1109/TAC.2010.2050352 [3] J. Deutscher and N. Gehring, Output feedback control of coupled linear parabolic ODE-PDE-ODE systems, IEEE Transactions on Automatic Control, 2021, 66(10), 4668–4683. [4] J. Deutscher, N. Gehring and R. Kern, Output feedback control of general linear heterodirectional hyperbolic ODE-PDE-ODE systems, Automatica, 2018, 95, 472–480. doi: 10.1016/j.automatica.2018.06.021 [5] J. Deutscher, N. Gehring and R. Kern, Output feedback control of general linear heterodirectional hyperbolic PDE-ODE systems with spatially-varying coefficients, International Journal of Control, 2019, 92(10), 2274–2290. doi: 10.1080/00207179.2018.1436770 [6] N. Gehring, A systematic backstepping design of tracking controllers for ode-pde-ode systems with nonlinear actuator dynamics, Advances in Distributed Parameter Systems, Springer, Cham, 2022, 171–196. [7] A. Hasan and S. X. Tang, Boundary control of a coupled Burgers' PDE-ODE system, International Journal of Robust and Nonlinear Control, 2022, 32(10), 5812–5836. doi: 10.1002/rnc.6145 [8] X. He, Y. Ma, M. Chen and W. He, Flight and vibration control of flexible air-breathing hypersonic vehicles under actuator faults, IEEE Transactions on Cybernetics, 2022, 53(5), 2741–2752. [9] M. Krstić, Compensating actuator and sensor dynamics governed by diffusion PDEs, Systems & Control Letters, 2009, 58(5), 372–377. [10] M. Krstić, Compensating a string PDE in the actuation or sensing path of an unstable ODE, IEEE Transactions on Automatic Control, 2009, 54(6), 1362–1368. doi: 10.1109/TAC.2009.2015557 [11] M. Krstić and A. Smyshlyaev, Boundary Control of PDEs: A Course on Backstepping Designs, Society for Industrial and Applied Mathematics, Philadelphia, PA, 2008. [12] J. Li and Y. Liu, Compensation of uncertain linear actuator dynamics for a class of cascaded PDE-ODE systems, Science China-Information Sciences, 2023, 66, 119204. doi: 10.1007/s11432-020-3194-9 [13] J. Li and Y. Liu, Adaptive control of uncertain coupled reaction-diffusion dynamics with equi-diffusivity in the actuation path of an ODE system, IEEE Transactions on Automatic Control, 2021, 66(2), 802–809. doi: 10.1109/TAC.2020.2981913 [14] J. Li and Y. Liu, Adaptive stabilization of coupled PDE-ODE systems with multiple uncertainties, ESAIM, Control, Optimisation Calculus Variations, 2014, 20(2), 488–516. doi: 10.1051/cocv/2013072 [15] J. Li, Z. Wu and Y. Liu, Adaptive stabilization for an uncertain reaction-diffusion equation with dynamic boundary condition at control end, Systems & Control Letters, 2022, 162, 105180. [16] J. Li, Z. Wu and C. Wen, Adaptive stabilization for a reaction-diffusion equation with uncertain nonlinear actuator dynamics, Automatica, 2021, 109594. [17] Y. -X. Li, X. Li and S. Tong, Backstepping-based fuzzy adaptive stabilization of reaction-diffusion equation with state constraints, IEEE Transactions on Cybernetics, 2024, 54(5), 3030–3038. DOI: 10.1109/TCYB.2022.3227899. [18] N. B. Liberis and M. Krstić, Compensating the distributed effect of diffusion and counter-convection in multi-input and multi-output LTI systems, IEEE Transactions on Automatic Control, 2011, 56(3), 637–643. doi: 10.1109/TAC.2010.2091187 [19] W. Liu and M. Krstić, Backstepping boundary control of Burgers' equation with actuator dynamics, Systems & Control Letters, 2000, 41(4), 291–303. [20] F. D. Meglio, P. O. Lamare and U. J. F. Aarsnes, Robust output feedback stabilization of an ODE-PDE-ODE interconnection, Automatica, 2020, 119, 109059. doi: 10.1016/j.automatica.2020.109059 [21] B. d'Andréa-Novel and J. M. Coron, Exponential stabilization of an overhead crane with flexible cable via a back-stepping approach, Automatica, 2000, 36(4), 587–593. doi: 10.1016/S0005-1098(99)00182-X [22] A. Smyshlyaev and M. Krstić, Closed-form boundary state feedbacks for a class of 1-D partial integro-differential equations, IEEE Transactions on Automatic Control, 2004, 49(12), 2185–2202. doi: 10.1109/TAC.2004.838495 [23] S. Tang and C. Xie, State and output feedback boundary control for a coupled PDE-ODE system, Systems & Control Letters, 2011, 60(8), 540–545. [24] J. Wang and M. Krstić, Output feedback boundary control of a heat PDE sandwiched between two ODEs, IEEE Transactions on Automatic Control, 2019, 64(11), 4653–4660. doi: 10.1109/TAC.2019.2901704 [25] J. Wang, M. Krstic and Y. Pi, Control of a $2\times2$ coupled linear hyperbolic ystem sandwiched between 2 ODEs, International Journal of Robust and Nonlinear Control, 2018, 28(13), 3987–4016. doi: 10.1002/rnc.4117 [26] J. Wang, J. Liu, B. Ren and J. Chen, Sliding mode control to stabilization of cascaded heat PDE-ODE systems subject to boundary control matched disturbance, Automatica, 2015, 52, 23–34. doi: 10.1016/j.automatica.2014.10.117 [27] Y. Xiao, Y. Yuan, C. Yang, B. Luo, X. Xu and S. Dubljevic, Adaptive neural tracking control of a class of hyperbolic pde with uncertain actuator dynamics, IEEE Transactions on Cybernetics, 2022, 54(2), 693–705. [28] Z. Zhen, Y. Si and C. Xie, Indirect control to stabilize reaction-diffusion equation, International Journal of Control, 2021, 94(11), 3091–3098. doi: 10.1080/00207179.2020.1750708 [29] H. Zhou, B. Guo and Z. Wu, Output feedback stabilization for a cascaded wave PDE-ODE system subject to boundary control matched disturbance, International Journal of Control, 2016, 89(12), 2396–2405. doi: 10.1080/00207179.2016.1158866 [30] Z. Zhou and C. Xu, Stabilization of a second order ode-heat system coupling at intermediate point, Automatica, 2015, 60, 57–64. doi: 10.1016/j.automatica.2015.06.039 -
-
-
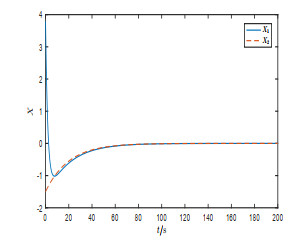
Figure 1.
Trajectory of system state
$ X $ -
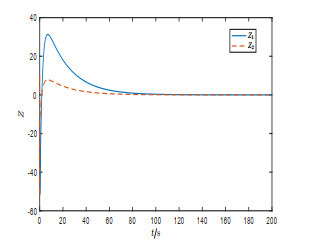
Figure 2.
Trajectory of system state
$ Z $ -
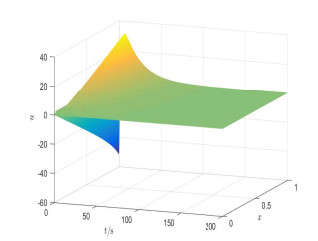
Figure 3.
Trajectory of system state
$ u $ -
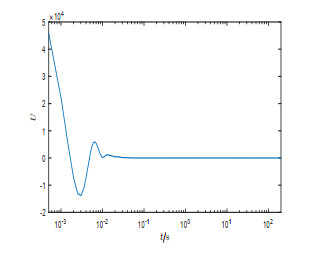
Figure 4.
Trajectory of control input
$ U $




 DownLoad:
DownLoad: