| Citation: | Lina Guo, Chengmin Hou, Mingzhe Sun. THE METHOD OF LOWER AND UPPER SOLUTIONS FOR FRACTIONAL DIFFERENTIAL SYSTEM WITH P-LAPLACIAN OPERATORS[J]. Journal of Applied Analysis & Computation, 2026, 16(1): 121-135. doi: 10.11948/20240584 |
THE METHOD OF LOWER AND UPPER SOLUTIONS FOR FRACTIONAL DIFFERENTIAL SYSTEM WITH P-LAPLACIAN OPERATORS
-
Abstract
This paper focuses on the multi-point boundary value problem for a nonlinear fractional differential system, involving p-Laplacian operator and integral boundary conditions, which arises from many complex processes such as the nonlinear phenomena in nonNewtonian fluids and mathematical modeling. Based on the monotone iterative technique, a new method of lower and upper solutions are proposed. Some new results on the existence of positive solutions for multi-point boundary value problem with integral boundary conditions are established. Finally, an example is presented to illustrate the wide range of potential applications of our main results.
-

-
References
[1] M. Azouzi and L. Guedda, Existence result for nonlocal boundary value problem of fractional order at resonance with p-Laplacian operator, Azerbaijan Journal of Mathematics, 2023, 13. [2] C. Bai, Existence and uniqueness of solutions for fractional boundary value problems with p-Laplacian operator, Adv. Differential Equations, 2018, 4(2018). DOI: 10.1186/s13662-017-1460-3. [3] F. Chabane, S. Abbas, M. Benbachir, et al., Existence of concave positive solutions for nonlinear fractional differential equation with p-Laplacian operator, Vietnam Journal of Mathematics, 2023, 51, 505-543. DOI: 10.1007/s10013-022-00552-9. [4] L. Guo, C. Li, N. Qiao and J. Zhao, Convergence analysis of positive solution for Caputo-Hadamard fractional differential equation, Nonlinear Analysis: Modelling and Control, 2025, 1-19. [5] L. Guo and L. Liu, Maximal and minimal iterative positive solutions for singular infinite-point p-Laplacian fractional differential equations, Nonlinear Anal. Model. Control, 2018, 23(6), 851-865. [6] L. Guo, L. Liu and Y. Wu, Iterative unique positive solutions for singular p-Laplacian fractional differential equation system with several parameters, Nonlinear Anal. Model. Control, 2018, 23(2), 182-203. [7] L. Guo, Y. Wang and C. Li, Solvability for a higher-order Hadamard fractional differential model with a sign-changing nonlinearity dependent on the parameter, Journal of Applied Analysis Computation, 2024, 14, 2762-2776. [8] L. Guo, Y. Wang and H. Liu, On iterative positive solutions for a class of singular infinite-point p-Laplacian fractional differential equation with singular source terms, Journal of Applied Analysis Computation, 2023, 13(5), 2827-2842. [9] L. Guo, J. Zhao, S. Dong and X. Hou, Existence of multiple positive solutions for Caputo fractional differential equation with infinite-point boundary value conditions, Journal of Applied Analysis and Computation, 2022, 12(5), 1786-1800. DOI: 10.11948/20210301. [10] L. Guo, J. Zhao, L. Liao and L. Liu, Existence of multiple positive solutions for a class of infinite-point singular p-Laplacian fractional differential equation with singular source terms, Nonlinear Anal. : Model. Control, 2022, 27(4), 609-629. [11] Z. Han, H. Lu and C. Zhang, Positive solutions for eigenvalue problems of fractional differential equation with generalized p-Laplacian, Appl. Math. Comput., 2015, 257, 526-536. [12] X. Hao, H. Wang, L. Liu and Y. Cui, Positive solutions for a system of nonlinear fractional nonlocal boundary value problems with parameters and p-Laplacian operator, Boundary Value Problem, 2017, 182. DOI: 10.1186/s13661-017-0915-5. [13] H. Jafari, D. Baleanu and H. Khan, Existence criterion for the solutions of fractional order p-Laplacian boundary value problems, Boundary Value Problem, 2015, 164, 1-10. [14] S. Li, X. Zhang, Y. Wu and L. Caccetta, Extremal solutions for p-Laplacian differential systems via iterative computation, Applied Mathematics Letters, 2013, 26, 1151-1158. [15] X. Liu, M. Jia and W. Ge, The method of lower and upper solutions for mixed fractional four-point boundary value problem with p-Laplacian operator, Applied Mathematics Letters, 2017, 65, 56-62. [16] X. Liu, M. Jia and X. Xiang, On the solvability of a fractional differential equation model involving the p-Laplacian operator, Comput. Math. Appl., 2012, 64, 3267-3275. [17] Y. Liu and X. Yang, Resonant boundary value problems for singular multi-term fractional differential equations, J. Differ. Equ. Appl., 2013, 5, 409-472. [18] T. Ren, S. Li, X. Zhang and L. Liu, Maximum and minimum solutions for a nonlocal p-Laplacian fractional differential system from eco-economical processes, Boundary Value Problem, 2017, 118. DOI: 10.1186/s13661-017-0849-y. [19] S. Rezapour, M. Abbas, S. Etemad, et al., On a multi-point p-Laplacian fragmental differential equation with generalized fragment difference, Mathematical Methods in the Applied Sciences, 2023, 46(7), 8390-8407. DOI: 10.1002/mma.8301. [20] W. Sun, Y. Su and X. Han, Existence of solutions for a coupled system of Caputo-Hadamard fractional differential equations with p-Laplacian operators, Journal of Applied Analysis and Computation, 2022, 1885-1900. DOI: 10.11948/20210384. [21] H. Wang and J. Jiang, Existence and multiplicity of positive solutions for a system of nonlinear fractional multi-point boundary value problems with p-laplacian operator, Journal of Applied Analysis and Computation, 2021, 351-366. DOI: 10.11948/20200021. [22] K. Wang and Q. Zhou, Multiple positive solutions for nonlinear eigenvalue problems involving p-Laplacian-Like Operators, Mediterr. J. Math., 2023, 334. DOI: 10.1007/s00009-023-02548-2. [23] Y. Wang and J. Jiang, Existence and nonexistence of positive solutions for the fractional coupled system involving generalized p-Laplacian, Adv. Differential Equations, 2017, 337. DOI: 10.1186/s13662-017-1385-x. [24] J. Wu, X. Zhang, L. Liu, Y. Wu and Y. Cui, The convergence analysis and error estimation for unique solution of a p-Laplacian fractional differential equation with singular decreasing nonlinearity, Boundary Value Problem, 2018, 82(2018). DOI: 10.1186/s13661-018-1003-1. [25] F. Yan, M. Zuo and X. Hao, Positive solution for a fractional singular boundary value problem with p-Laplacian operator, Boundary Value Problem, 2018, 51. DOI: 10.1186/s13661-018-0972-4. [26] X. Zhang, L. Liu, B. Wiwatanapataphee and Y. Wu, The eigenvalue for a class of singular p-Laplacian fractional differentialequations involving the Riemann-Stieltjes integral boundary condition, Appl. Math. Comput., 2014, 235, 412-422. -
-
-
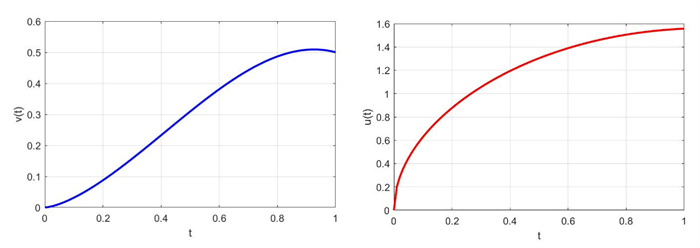
Figure 1.
The approximate solution of the system.




 DownLoad:
DownLoad: