| Citation: |
Jiarui Zhang, Wei Li, Mi Wang. ANALYSIS OF THE KINETIC PROPERTIES OF THE DISCRETE FOREST DISEASE AND INSECT PEST MODELS[J]. Journal of Applied Analysis & Computation, 2026, 16(1): 136-154. doi: 10.11948/20240542
|
ANALYSIS OF THE KINETIC PROPERTIES OF THE DISCRETE FOREST DISEASE AND INSECT PEST MODELS
-
Abstract
In this paper, we study the dynamic behavior of discrete forest disease and pest model-spruce aphid model, analyze the properties of the dynamics by using the difference equation theory, including the existence of equilibrium points in the system model, and further analyze the stability and instability conditions of these equilibrium points. In addition, the step h is selected as the bifurcation parameter using the central manifold theorem to analyze the Flip bifurcation and Hopf bifurcation at the equilibrium point, and prove the chaos of the system through the maximum Lyapunov diagram. In order to verify the theoretical proof, the system model is simulated numerically to draw relevant conclusions.
-
-
References
[1] Y. Bai, L. Wang and X. Yuan, Pesticide control, physical control, or biological control, How to manage forest pests and diseases more effectively, Front. Ecol. Evol., 2023, 11. DOI: 10.3389/fevo.2023.1200268. [2] D. Bevacqua, I. Grechi, M. Génard, et al., The consequences of aphid infestation on fruit production become evident in a multi-year perspective: Insights from a virtual experiment, Ecol. Model., 2016, 338, 11-16. [3] S. J. Crute, Computer simulations of green spruce aphid populations, J. Anim. Ecol., 1992. [4] B. Dalziel, E. Thomann and J. Medlock, Global analysis of a predator-prey model with variable predator search rate, J. Math. Biol., 2020, 81(1), 159-183. [5] K. R. Day, H. Armour and M. Docherty, Population responses of a conifer‐dwelling aphid to seasonal changes in its host, Ecol. Entomol., 2004, 29(5), 555-565. [6] K. R. Day, M. P. Ayres, R. Harrington, et al., Interannual dynamics of aerial and arboreal green spruce aphid populations, Popul. Ecol., 2010, 52, 317-327. [7] S. A. Estay, M. Lima, F. A. Labra, et al., Increased outbreak frequency associated with changes in the dynamic behaviour of populations of two aphid species, Oikos, 2012, 121(4), 614-622. [8] B. Hong and C. Zhang, Bifurcations and chaotic behavior of a predator-prey model with discrete time, AIMS Math., 2023, 8(6), 13390-13410. [9] Y. L. Huang, W. Y. Shi and S. W. Zhang, A stochastic predator-prey model with Holling Ⅱ increasing function in the predator, J. Biol. Dyn., 2021, 15(1), 1-18. [10] S. R. J. Jang and D. M. Johnson, Dynamics of discrete-time larch budmoth population models, J. Biol. Dyn., 2009, 3(2-3), 209-223. [11] L. Ji, Z. Wang, X. Wang, et al., Forest insect pest management and forest management in China: An overview, Environ. Manage., 2011, 48, 1107-1121. [12] J. T. Jones, M. Moens, M. Mota, et al., Bursaphelenchus xylophilus: Opportunities in comparative genomics and molecular host–parasite interactions, Mol. Plant Pathol., 2008, 9(3), 357-368. [13] G. Lemperiere, K. R. Day, Y. Petit‐Berghem, et al., Interannual population dynamics of the green spruce aphid Elatobium abietinum (Walker) in France, Ann. Appl. Biol., 2020, 176(3), 233-240. [14] A. H. Li, H. Y. Jing and J. C. Fu, Dynamic characteristic of spruce budworm–its natural enemy–pesticide interaction model, J. Biomathem., 2006, 21(3), 377-383. [15] T. Li, X. Zhang and C. Zhang, Pattern dynamics analysis of a space–time discrete spruce budworm model, Chaos. Solitons. Fractals., 2024, 179, 114423. [16] L. Liang, S. Niu and J. Wang, Current situation and future study on effect of invading Bursaphelenchus xylophilus on ecosystem, J. Zhejiang For. Sci. Technol., 2006, 73-78. [17] M. Lima, R. Harrington, S. Saldaña, et al., Non‐linear feedback processes and a latitudinal gradient in the climatic effects determine green spruce aphid outbreaks in the UK, Oikos, 2008, 117(6), 951-959. [18] D. Ludwig, D. D. Jones and C. S. Holling, Qualitative analysis of insect outbreak systems: The spruce budworm and forest, J. Anim. Ecol., 1978, 47(1), 315-332. [19] C. W. Luo and K. Li, The relation of species diversity to pest control in forest plantations, Sci. Silv. Sin., 2006, 109-115. [20] A. Rasmussen, J. Wyller and J. O. Vik, Relaxation oscillations in spruce–budworm interactions, nonlinear analysis: Real world applications, Chin. J. Biol. Control, 2011, 304-319. [21] S. Redlich, J. Clemens, M. K. F. Bader, et al., Identifying new associations between invasive aphids and Pinaceae trees using plant sentinels in botanic gardens, Biol. Invas., 2019, 21, 217-228. [22] J. H. M. Thornley and J. A. Newman, Climate sensitivity of the complex dynamics of the green spruce aphid—Spruce plantation interactions: Insight from a new mechanistic model, Plos. One, 2022, 17(2), e0252911. [23] D. W. Williams and A. M. Liebhold, Spatial scale and the detection of density dependence in spruce budworm outbreaks in eastern North America, Oecologia, 2000, 124, 544-552. [24] D. W. Williams and A. M. Liebhold, Spatial synchrony of spruce budworm outbreaks in eastern North America, Ecology, 2000, 81(10), 2753-2766. [25] H. C. Xu and Y. Q. Luo, Ecosystems attacked by Bursaphelenchus xylophilus: A review, J. Zhejiang For. Coll., 2010, 27(3), 445-450. [26] J. Xu and S. Yuan, Near‐optimal control of a stochastic pine wilt disease model with prevention strategies, Math. Methods Appl. Sci., 2023, 46(13), 13855-13881. [27] Q. Xu and C. Zhang, Bifurcation analysis and chaos of a modified Holling-Tanner model with discrete time, J. Appl. Anal. Comput., 2024, 14(6), 3425-3449. [28] W. Xu, S. Chen and L. Chen, Modeling of the prevention and control of forest pest, J. Biol. Syst., 2007, 15(04), 539-550. [29] M. Yang, M. Li, L. Qu, et al., Advances in research on pathogenic microorganisms of pine sawfly, Chin. J. Biol. Control, 2007, 23(3), 284-289. [30] Z. Yang, X. Wang, Y. Zhang, et al., Research advances of Chinese major forest pests by integrated management based on biological control, Chin. J. Biol. Control., 2018, 34(2), 163. [31] X. Zhang, C. Zhang and Y. Zhang, Pattern dynamics analysis of a time-space discrete FitzHugh-Nagumo (FHN) model based on coupled map lattices, Comput. Math. Appl., 2024, 157, 92-123. [32] X. Zhang, C. Zhang and Y. Zhang, Discrete kinetic analysis of a general reaction-diffusion model constructed by Euler discretization and coupled map lattices, Math. Comput. Simul., 2024, 1218-1236. [33] J. Zhao and Y. Yan, Stability and bifurcation analysis of a discrete predator–prey system with modified Holling–Tanner functional response, Adv. Differ. Equ., 2018, 2018(1), 402. [34] J. Zheng, Y. Xu, H. Zhang, et al., Advances and prospects of target recognition techniques for forest pest control at home and abroad, Sci. Silv. Sin., 2023, 152-166. -
-
Figures(6)
Export File
Citation
Jiarui Zhang, Wei Li, Mi Wang. ANALYSIS OF THE KINETIC PROPERTIES OF THE DISCRETE FOREST DISEASE AND INSECT PEST MODELS[J]. Journal of Applied Analysis & Computation, 2026, 16(1): 136-154. doi: 10.11948/20240542
Format
Content
DownLoad:
-
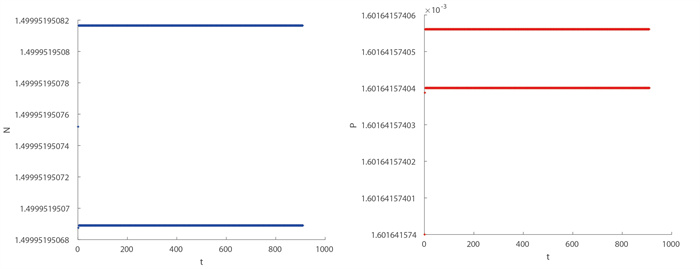
Figure 1.
The graph of N, S when Flip bifurcation occurs at k = 10000, η = 7.54, β = 14.96, ρ = 0.9, h = 0.262122270347572, Smax = 50, δ = 0.6, r = 10, B(N0, S0) = (1.499951950752, 0.001601641574).
-
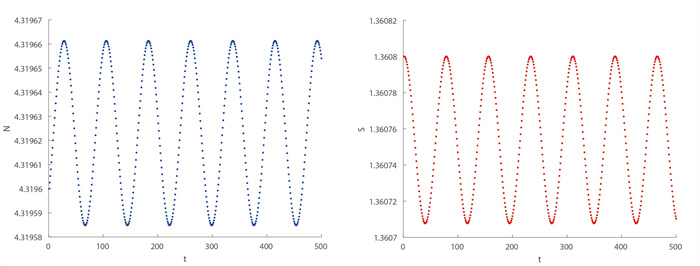
Figure 2.
The graph of N, S when Hopf bifurcation occurs at k = 50000, η = 1.54, β = 5.77, ρ = 1, h = 0.087593294844698, Smax = 10, δ = 0.9, r = 5, (N0, S0) = (4.319623064185476, 1.360753871629049).
-
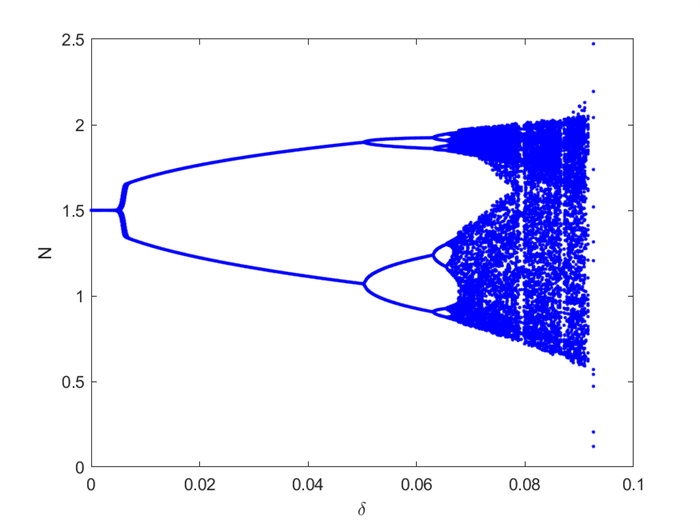
Figure 3.
The Flip bifurcation is chaotic with the parameters k = 10000, η = 7.54, β = 14.97, ρ = 0.9, h = 0.262122270347572, Smax = 50, δ = 0.6, r = 10, B(N0, S0) = (1.499951950752, 0.001601641574).
-
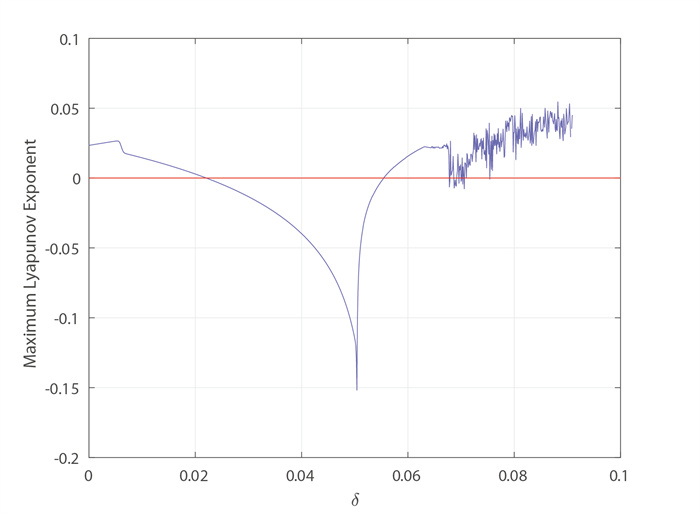
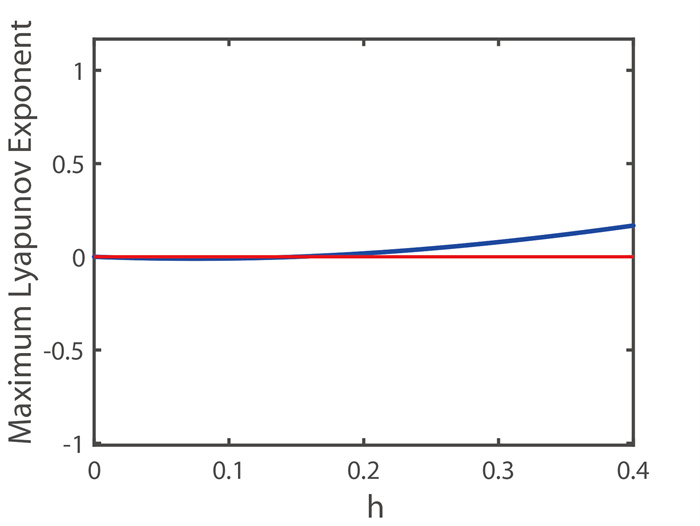
Figure 4.
The parameters in the figure are the maximum Lyapunov exponential map where k = 10000, η = 7.54, β = 14.97, ρ = 0.9, h = 0.262122270347572, Smax = 50, δ = 0.6, r = 10, B(N0, S0) = (1.499951950752, 0.001601641574).
-
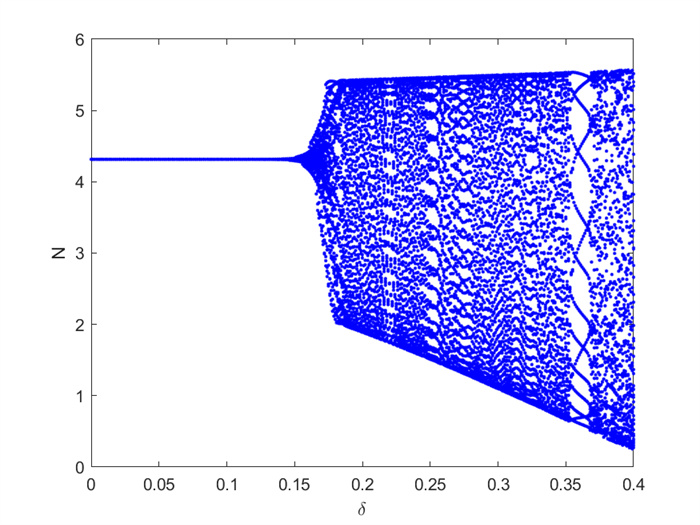
Figure 5.
The Hopf bifurcation is chaotic with the parameters
$ k = 50000 $ $ \eta = 3.72 $ $ \beta = 8.47 $ $ \rho = 1 $ $ h = 0.149687409244297 $ $ {S_{\max }} = 10 $ $ \delta = 0.9 $ $ r = 5 $ $ B\left( {{N_0},{S_0}} \right) = \left( {4.3149528055,1.3700943889} \right) $ -
Figure 6.
The parameters in the figure are the maximum Lyapunov exponential map where
$ k = 50000 $ $ \eta = 3.72 $ $ \beta = 8.47 $ $ \rho = 1 $ $ h = 0.149687409244297 $ $ {S_{\max }} = 10 $ $ \delta = 0.9 $ $ r = 5 $ $ B\left( {{N_0},{S_0}} \right) = \left( {4.3149528055,1.3700943889} \right) $