| Citation: | Rong Wu. TWO-DIMENSIONAL SOLITARY WAVE SOLUTIONS FOR WATER WAVES NEAR THE CRITICAL POINT[J]. Journal of Applied Analysis & Computation, 2025, 15(6): 3504-3520. doi: 10.11948/20250017 |
TWO-DIMENSIONAL SOLITARY WAVE SOLUTIONS FOR WATER WAVES NEAR THE CRITICAL POINT
-
Abstract
This paper considers that the Bond number is greater than but close to $\frac{1}{3} $ and the Froude number is greater than but close to 1 for the two-dimensional traveling gravity-capillary waves in water of finite depth. The horizontal propagating direction and the stream function are chosen as independent variables. The Euler equations are reduced to a system of ordinary differential equations with dimension 4 by applying a spatial dynamics approach, a center manifold reduction and a normal form analysis. The reduced system has a homoclinic solution near a nonzero equilibrium. The fixed point theorem shows that this homoclinic solution persists for the original system, i.e., the hydrodynamic problem has a solitary wave solution which exponentially approaches a constant function (independent of the horizontal variable but dependent on the stream function) at infinity.
-
Keywords:
- Solitary wave solutions /
- center manifold reduction /
- normal form /
- homoclinic orbits
-

-
References
[1] C. J. Amick and K. Kirchgässner, A theory of solitary water-waves in the presence of surface tension, Arch. Rat. Mech. Anal., 1989, 105, 1-49. doi: 10.1007/BF00251596 [2] J. T. Beale, Exact solitary water waves with capillary ripples at infinity, Comm. Pure Appl. Math., 1991, 44, 211-257. doi: 10.1002/cpa.3160440204 [3] B. Buffoni, A. R. Champneys and J. F. Toland, Bifurcation and coalescence of a plethora of homoclinic orbits for a Hamiltonian system, J. Dynamics and Diff. Eqns., 1996, 8, 221-281. doi: 10.1007/BF02218892 [4] B. Buffoni and M. D. Groves, A multiplicity result for solitary gravity-capillary waves in deep water via critical-point theory, Arch. Ration. Mech. Anal., 1999, 146, 183-220. doi: 10.1007/s002050050141 [5] B. Buffoni, M. D. Groves and J. F. Toland, A plethora of solitary gravity-capillary water waves with nearly critical Bond and Froude numbers, Philos. Trans. Roy. Soc. London Ser. A, 1996, 354, 575-607. doi: 10.1098/rsta.1996.0020 [6] E. A. Coddington and N. Levinson, Theory of Ordinary Differential Equations, McGraw-Hill, New York, 1995. [7] J. Cui, G. Gao and S. M. Sun, Controllability and stabilization of gravity-capillary surface water waves in a basin, Commun. Pure Appl. Anal., 2022, 21, 2035-2063. doi: 10.3934/cpaa.2021158 [8] S. Deng and S. M. Sun, Three-dimensional gravity-capillary waves on water-Small surface tension case, Phys. D, 2009, 238, 1735-1751. doi: 10.1016/j.physd.2009.05.012 [9] S. Deng and S. M. Sun, Exact two-dimensional multi-hump waves on water of finite depth with small surface tension, Arch. Rational Mech. Anal., 2020, 236, 451-503. doi: 10.1007/s00205-019-01474-6 [10] F. Dias and G. Iooss, Capillary-gravity solitary waves with damped oscillations, Phys. D, 1993, 65, 399-423. doi: 10.1016/0167-2789(93)90064-8 [11] L. Du and Y. Yang, The free boundary of steady axisymmetric inviscid flow with vorticity I: Near the degenerate point, Comm. Math. Phys., 2023, 400, 2137-2179. doi: 10.1007/s00220-023-04651-7 [12] L. Du and Y. Yang, The free boundary of steady axisymmetric inviscid flow with vorticity Ⅱ: Near the non-degenerate points, Comm. Math. Phys., 2024, 405, Paper No. 262, 58 pp. [13] C. Elphick, E. Tirapegui, M. E. Brachet, P. Coullet and G. Iooss, A simple global characterization for normal forms of singular vector fields, Phys. D, 1987, 29, 95-127. doi: 10.1016/0167-2789(87)90049-2 [14] G. Franzina, Boundary vorticity of incompressible 2D flows, Z. Angew. Math. Phys., 2024, 75, Paper No. 198, 13 pp. [15] M. D. Groves and A. Mielke, A spatial dynamics approach to three-dimensional gravity-capillary steady water waves, Proc. Roy. Soc. Edinburgh Sect., 2001, 131A, 83-136. [16] M. Haragus, T. Truong and E. Wahlén, Transverse dynamics of two-dimensional traveling periodic gravity-capillary water waves, Water Waves, 2023, 5, 65-99. doi: 10.1007/s42286-023-00074-y [17] G. Iooss, A codimension 2 bifurcation for reversible vector fields, Fields Inst. Comm., 1995, 4, 201-217. [18] G. Iooss and M. Adelmeyer, Topics in Bifurcation Theory and Applications, World Scientific, Singapore, 1992. [19] G. Iooss and K. Kirchgässner, Bifurcation d'ondes solitaires en présence d'une faible tension superficielle, C. R. Acad. Sci. Paris Sér. I Math., 1990, 311, 265-268. [20] G. Iooss and K. Kirchgässner, Water waves for small surface tension: An approach via normal form, Proc. Royal Soc. Edinburgh Sect., 1992, 122A, 267-299. [21] G. Iooss and M. C. Pérouème, Perturbed homoclinic solutions in reversible 1: 1 resonance vector fields, J. Diff. Equ., 1993, 102, 62-88. doi: 10.1006/jdeq.1993.1022 [22] H. Kielhöfer, Bifurcation Theory: An Introduction with Applications to PDEs, Springer, New York, 2003. [23] K. Kirchgässner, Nonlinearly resonant surface waves and homoclinic bifurcation, Adv. in Appl. Mech., 1988, 26, 135-181. [24] E. Lombardi, Orbits homoclinic to exponentially small periodic orbits for a class of reversible systems. Application to water waves, Arch. Rat. Mech. Anal., 1997, 137, 227-304. doi: 10.1007/s002050050029 [25] A. Mielke, Reduction of quasilinear elliptic equations in cylindrical domains with applications, Math. Mech. Appl. Sci., 1988, 10, 51-66. doi: 10.1002/mma.1670100105 [26] D. Svensson Seth, Internal doubly periodic gravity-capillary waves with vorticity, SIAM J. Math. Anal., 2024, 56, 7545-7575. doi: 10.1137/23M1556319 [27] S. M. Sun, Existence of a generalized solitary wave solution for water with positive Bond number smaller than 1/3, J. Math. Anal. Appl., 1991, 156, 471-504. doi: 10.1016/0022-247X(91)90410-2 [28] S. M. Sun and M. Shen, A new solitary wave solution for water waves with surface tension, Ann. Mat. Pura Appl., 1992, 162, 179-214. doi: 10.1007/BF01760005 [29] W. Walter, Gewöhnliche Differentialgleichungen, Springer, New York, 1972. [30] H. Zhu, Propagation of singularities for gravity-capillary water waves, Anal. PDE, 2024, 17, 281-344. doi: 10.2140/apde.2024.17.281 -
-
-
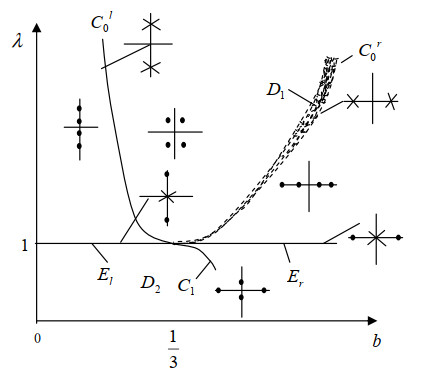
Figure 1.
The distribution of the important eigenvalues of the linearized operator. The number of purely imaginary eigenvalues varies near the curves
$ C_0^l,E_l $ $ E_r $




 DownLoad:
DownLoad: