| Citation: |
Xiaohui Ai, Wufei Huang, Yifan Wu. ANALYSIS OF A STOCHASTIC TREE-GRASS MODEL WITH MEAN-REVERTING ORNSTEIN-UHLENBECK PROCESS[J]. Journal of Applied Analysis & Computation, 2025, 15(6): 3521-3534. doi: 10.11948/20230470
|
ANALYSIS OF A STOCHASTIC TREE-GRASS MODEL WITH MEAN-REVERTING ORNSTEIN-UHLENBECK PROCESS
-
Abstract
Considering the survival regulation mechanisms of trees and grasses in savannas ecosystems, the stochastic variability of ecosystems and the effects of fire, a stochastic tree-grass model with mean-reverting Ornstein-Uhlenbeck process is developed and investigated in this paper. Firstly, the biological and environmental components of the tree-grass model and the biological significance of each parameter are described, while the mean-reverting Ornstein-Uhlenbeck process is introduced and its biological significance is explained. Then we list some dynamical properties of the model and give proofs. The existence and moment estimates of the global solution of the stochastic model and sufficient conditions for the existence of a stationary distribution are given. In addition, we give sufficient conditions for extinction of species. Finally, we verify that the theories are valid by numerical simulation.
-
-
References
[1] D. J. Augustine, J. Ardo, C. J. Feral, et al., Determinants of woody cover in african savannas, 2005. [2] Y. Cai, J. Jiao, Z. Gui, et al., Environmental variability in a stochastic epidemic model, Applied Mathematics and Computation, 2018, 329, 210–226. doi: 10.1016/j.amc.2018.02.009 [3] D. J. Higham, An algorithmic introduction to numerical simulation of stochastic differential equations, SIAM Review, 2001, 43(3), 525–546. doi: 10.1137/S0036144500378302 [4] C. Ji, D. Jiang and J. Fu, Rich dynamics of a stochastic Michaelis–Menten-type ratio-dependent predator–prey system, Physica A: Statistical Mechanics and its Applications, 2019, 526, 120803. doi: 10.1016/j.physa.2019.04.039 [5] W. Ji, Y. Zhang and M. Liu, Dynamical bifurcation and explicit stationary density of a stochastic population model with allee effects, Applied Mathematics Letters, 2021, 111, 106662. doi: 10.1016/j.aml.2020.106662 [6] R. Khasminskii, Stochastic Stability of Differential Equations, 66, Springer Science & Business Media, Berlin, 2011. [7] X. Li and X. Mao, Population dynamical behavior of non-autonomous Lotka-Volterra competitive system with random perturbation, Discrete and Continuous Dynamical Systems, 2009, 24(2), 523–593. doi: 10.3934/dcds.2009.24.523 [8] R. S. Liptser, A strong law of large numbers for local martingales, Stochastics, 1980, 3(1–4), 217–228. [9] M. Liu and M. Deng, Analysis of a stochastic hybrid population model with allee effect, Applied Mathematics and Computation, 2020, 364, 124582. doi: 10.1016/j.amc.2019.124582 [10] Q. Liu and D. Jiang, Stationary distribution and extinction of a stochastic predator–prey model with distributed delay, Applied Mathematics Letters, 2018, 78, 79–87. doi: 10.1016/j.aml.2017.11.008 [11] Q. Liu and D. Jiang, Influence of the fear factor on the dynamics of a stochastic predator–prey model, Applied Mathematics Letters, 2021, 112, 106756. doi: 10.1016/j.aml.2020.106756 [12] Q. Liu, D. Jiang, T. Hayat and A. Alsaedi, Dynamics of a stochastic predator–prey model with stage structure for predator and holling type ii functional response, Journal of Nonlinear Science, 2018, 28, 1151–1187. doi: 10.1007/s00332-018-9444-3 [13] X. Mao, G. Marion and E. Renshaw, Environmental brownian noise suppresses explosions in population dynamics, Stochastic Processes and their Applications, 2002, 97(1), 95–110. doi: 10.1016/S0304-4149(01)00126-0 [14] R. J. Scholes and S. R. Archer, Tree-grass interactions in savannas, Annual Review of Ecology and Systematics, 1997, 28(1), 517–544. doi: 10.1146/annurev.ecolsys.28.1.517 [15] A. Tamen Tchuinte, J. J. Tewa, P. Couteron, et al., A generic modeling of fire impact in a tree-grass savanna model, BIOMATH, 2014, 3(2). [16] X. Zhang and R. Yuan, A stochastic chemostat model with mean-reverting Ornstein-Uhlenbeck process and Monod-Haldane response function, Applied Mathematics and Computation, 2021, 394, 125833. doi: 10.1016/j.amc.2020.125833 [17] Y. Zhao, S. Yuan and J. Ma, Survival and stationary distribution analysis of a stochastic competitive model of three species in a polluted environment, Bulletin of Mathematical Biology, 2015, 77, 1285–1326. doi: 10.1007/s11538-015-0086-4 [18] B. Zhou, D. Jiang and T. Hayat, Analysis of a stochastic population model with mean-reverting Ornstein-Uhlenbeck process and allee effects, Communications in Nonlinear Science and Numerical Simulation, 2022, 111, 106450. doi: 10.1016/j.cnsns.2022.106450 -
-
Figures(4) / Tables(2)
Export File
Citation
Xiaohui Ai, Wufei Huang, Yifan Wu. ANALYSIS OF A STOCHASTIC TREE-GRASS MODEL WITH MEAN-REVERTING ORNSTEIN-UHLENBECK PROCESS[J]. Journal of Applied Analysis & Computation, 2025, 15(6): 3521-3534. doi: 10.11948/20230470
Format
Content
DownLoad:
-
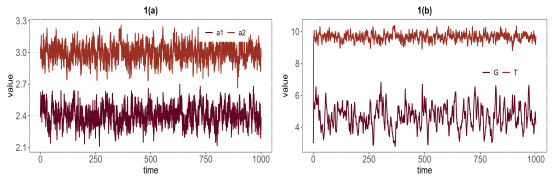
Figure 1.
The existence of global solution.
-
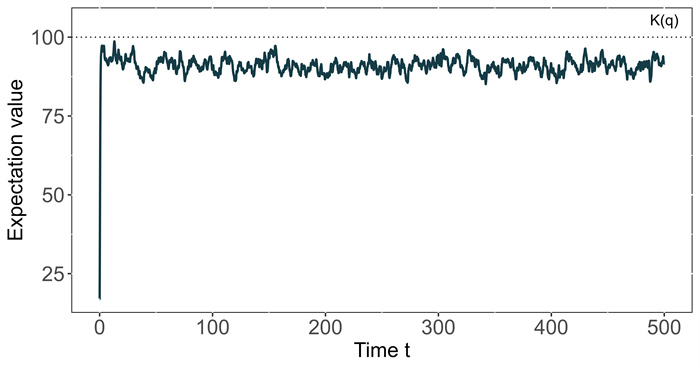
Figure 2.
Boundness of
$ \theta th $ -
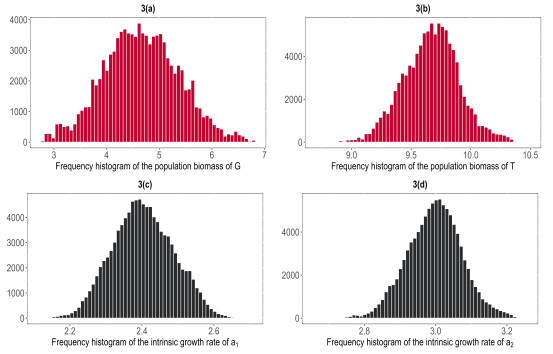
Figure 3.
Frequency histogram of solutions.
-
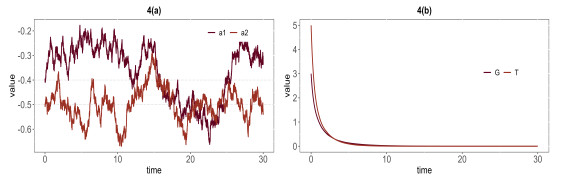
Figure 4.
Extinction of solutions.