| Citation: |
Azzh Saad Alshehry, Saima Noor, Abdulkafi Mohammed Saeed, Ahmad Shafee, Rasool Shah. INNOVATIVE SOLUTIONS FOR FRACTIONAL WHITHAM-BROER-KAUP MODEL USING TRANSFORM-BASED METHODS[J]. Journal of Applied Analysis & Computation, 2025, 15(6): 3805-3825. doi: 10.11948/20250039
|
INNOVATIVE SOLUTIONS FOR FRACTIONAL WHITHAM-BROER-KAUP MODEL USING TRANSFORM-BASED METHODS
-
Abstract
This study investigates the application of the Elzaki Residual Power Series Method (ERPSM) and the New Iteration Transform Method (NITM) for solving fractional-order Whitham-Broer-Kaup system. These nonlinear fractional differential equations are fundamental models for describing complex wave dynamics and fluid mechanics phenomena. Using the fractional derivative by the proposed methods provides robust and efficient approaches for deriving analytical solutions regarding power series and other functional forms. The convergence and reliability of the methods are thoroughly analyzed, highlighting their ability to handle the intricate dynamics of fractionalorder systems. Numerical simulations and illustrative examples validate the accuracy and effectiveness of ERPSM and NITM in solving fractional-order Whitham-Broer-Kaup system. The findings demonstrate the potential of these methods to address a wide range of problems in mathematical physics, fluid dynamics, and nonlinear wave theory, offering new insights into fractional-order modeling.
-
-
References
[1] G. Adomian, Solving Frontier Problems of Physics: The Decomposition Method (Vol. 60), Springer Science and Business Media, 2013. [2] A. El-Ajou, Adapting the Laplace transform to create solitary solutions for the nonlinear time-fractional dispersive PDEs via a new approach, The European Physical Journal Plus, 2021, 136(2), 229. [3] A. El-Ajou, O. A. Arqub and S. Momani, Approximate analytical solution of the nonlinear fractional KdV-Burgers equation: A new iterative algorithm, Journal of Computational Physics, 2015, 293, 81-95. [4] A. El-Ajou, O. A. Arqub and S. Momani, Approximate analytical solution of the nonlinear fractional KdV-Burgers equation: A new iterative algorithm, Journal of Computational Physics, 2015, 293, 81-95. [5] A. El-Ajou and Z. Al-Zhour, A vector series solution for a class of hyperbolic system of Caputo time-fractional partial differential equations with variable coefficients, Frontiers in Physics, 2021, 9, 525250. [6] A. Akgul, A novel method for a fractional derivative with non-local and non-singular kernel, Chaos, Solitons and Fractals, 2018, 114, 478-482. [7] E. K. Akgul, Solutions of the linear and nonlinear differential equations within the generalized fractional derivatives, Chaos: An Interdisciplinary Journal of Nonlinear Science, 2019, 29(2). [8] A. A. Alderremy, N. Iqbal, S. Aly and K. Nonlaopon, Fractional series solution construction for nonlinear fractional reaction-diffusion Brusselator model utilizing Laplace residual power series, Symmetry, 2022, 14(9), 1944. [9] A. Ali, K. Shah and R. A. Khan, Numerical treatment for traveling wave solutions of fractional Whitham-Broer-Kaup equations, Alexandria Engineering Journal, 2018, 57(3), 1991-1998. [10] M. Alqhtani, K. M. Saad, R. Shah and W. M. Hamanah, Discovering novel soliton solutions for (3+1)-modified fractional Zakharov-Kuznetsov equation in electrical engineering through an analytical approach, Optical and Quantum Electronics, 2023, 55(13), 1149. [11] M. Alqhtani, K. M. Saad, R. Shah, W. Weera and W. M. Hamanah, Analysis of the fractional-order local Poisson equation in fractal porous media, Symmetry, 2022, 14(7), 1323. [12] A. Atangana, Fractal-fractional differentiation and integration: Connecting fractal calculus and fractional calculus to predict complex system, Chaos, Solitons and Fractals, 2017, 102, 396-406. [13] D. Baleanu, K. Diethelm, E. Scalas and J. J. Trujillo, Fractional Calculus: Models and Numerical Methods (Vol. 3), World Scientific, 2012. [14] W. Bao, H. Liu, F. Wang, J. Du, Y. Wang, H. Li and X. Ye, Keyhole critical failure criteria and variation rule under different thicknesses and multiple materials in K-TIG welding, Journal of Manufacturing Processes, 2024, 126, 48-59. [15] S. Bhalekar and V. Daftardar-Gejji, New iterative method: Application to partial differential equations, Applied Mathematics and Computation, 2008, 203(2), 778-783. [16] M. Caputo, Linear models of dissipation whose Q is almost frequency independent-Ⅱ, Geophysical Journal International, 1967, 13(5), 529-539. [17] M. Caputo and M. Fabrizio, A new definition of fractional derivative without singular kernel, Progress in Fractional Differentiation and Applications, 2015, 1(2), 73-85. [18] X. Chen and R. Jing, Video super resolution based on deformable 3D convolutional group fusion, Scientific Reports, 2025, 15(1), 9050. DOI: 10.1038/s41598-025-93758-z. [19] J. Du, H. Liu, F. Wang, W. Bao and H. Li, Solidification microstructure reconstruction and its effects on phase transformation, grain boundary transformation mechanism, and mechanical properties of TC4 alloy welded joint, Metallurgical and Materials Transactions A, 2024, 55(4), 1193-1206. [20] E. M. Elsayed, R. Shah and K. Nonlaopon, The analysis of the fractional-order Navier-Stokes equations by a novel approach, Journal of Function Spaces, 2022, 2022(1), 8979447. [21] T. M. Elzaki, The new integral transform Elzaki transform, Global Journal of Pure and Applied Mathematics, 2011, 7(1), 57-64. [22] T. Eriqat, A. El-Ajou, N. O. Moa'ath, Z. Al-Zhour and S. Momani, A new attractive analytic approach for solutions of linear and nonlinear neutral fractional pantograph equations, Chaos, Solitons and Fractals, 2020, 138, 109957. [23] T. Eriqat, M. A. N. Oqielat, Z. Al-Zhour, A. El-Ajou and A. S. Bataineh, Revisited Fisher's equation and logistic system model: A new fractional approach and some modifications, International Journal of Dynamics and Control, 2023, 11(2), 555-563. [24] V. Daftardar-Gejji and S. Bhalekar, Solving fractional diffusion-wave equations using a new iterative method, Fractional Calculus and Applied Analysis, 2008, 11(2), 193-202. [25] V. Daftardar-Gejji and H. Jafari, An iterative method for solving nonlinear functional equations, Journal of Mathematical Analysis and Applications, 2006, 316(2), 753-763. [26] V. Daftardar-Gejji and H. Jafari, An iterative method for solving nonlinear functional equations, Journal of Mathematical Analysis and Applications, 2006, 316(2), 753-763. [27] S. Guo, Y. Li and D. Wang, 2-term extended RotaBaxter pre-lie-algebra and non-abelian extensions of extended RotaBaxter pre-lie algebras, Results in Mathematics, 2025, 80(3), 96. DOI: 10.1007/s00025-025-02411-8. [28] J. H. He, Homotopy perturbation technique, Computer methods in Applied Mechanics and Engineering, 1999, 178(3-4), 257-262. [29] J. H. He, Approximate analytical solution for seepage flow with fractional derivatives in porous media, Computer Methods in Applied Mechanics and Engineering, 1998, 167(1-2), 57-68. [30] Z. Huang, X. Zheng, C. Li, E. L. Tan, Z. Chen, L. Shi and B. Chen, Piecewise calculation scheme for the unconditionally stable Chebyshev finite-difference time-domain method, IEEE Transactions on Microwave Theory and Techniques, 2025, 1-9. DOI: 10.1109/TMTT.2025.3532330. [31] E. Keshavarz, Y. Ordokhani and M. Razzaghi, Bernoulli wavelet operational matrix of fractional order integration and its applications in solving the fractional order differential equations, Applied Mathematical Modelling, 2014, 38(24), 6038-6051. [32] A. A. Kilbas, H. M. Srivastava and J. J. Trujillo, Theory and applications of fractional differential equations, Elsevier, 2006, 204. [33] J. Li, X. Zhu, C. Feng, M. Wen and Y. Zhang, A simple and efficient three-dimensional spring element model for pore seepage problems, Engineering Analysis with Boundary Elements, 2025, 176, 106225. [34] K. Liu, S. Jiao, G. Nie, H. Ma, B. Gao, C. Sun and G. Wu, On image transformation for partial discharge source identification in vehicle cable terminals of high-speed trains, High Voltage, 2024, 9(5), 1090-1100. DOI: 10.1049/hve2.12487. [35] C. Ma, R. Mu, M. Li, J. He, C. Hua, L. Wang, J. Liu, G. Totis, J. Yang, K. Liu and Y. Zhou, A multi-scale spatial temporal interaction fusion network for digital twin-based thermal error compensation in precision machine tools, Expert Systems with Applications, 2025, 127812. [36] A. M. Malik and O. H. Mohammed, Two efficient methods for solving fractional Lane-Emden equations with conformable fractional derivative, Journal of the Egyptian Mathematical Society, 2020, 28, 1-11. [37] N. O. Moa'ath, A. El-Ajou, Z. Al-Zhour, T. Eriqat and M. Al-Smadi, A new approach to solving fuzzy quadratic Riccati differential equations, International Journal of Fuzzy Logic and Intelligent Systems, 2022, 22(1), 23-47. [38] M. Naeem, O. F. Azhar, A. M. Zidan, K. Nonlaopon and R. Shah, Numerical analysis of fractional-order parabolic equations via Elzaki transform, Journal of Function Spaces, 2021, 2021(1), 3484482. [39] M. Naeem, H. Rezazadeh, A. A. Khammash and S. Zaland, Analysis of the fuzzy fractional-order solitary wave solutions for the KdV equation in the sense of Caputo-Fabrizio derivative, Journal of Mathematics, 2022, 2022(1), 3688916. [40] K. Nonlaopon, M. Naeem, A. M. Zidan, R. Shah, A. Alsanad and A. Gumaei, Numerical investigation of the time-fractional Whitham-Broer-Kaup equation involving without singular kernel operators, Complexity, 2021, 2021(1), 7979365. [41] M. A. N. Oqielat, T. Eriqat, Z. Al-Zhour, O. Ogilat, A. El-Ajou and I. Hashim, Construction of fractional series solutions to nonlinear fractional reaction-diffusion for bacteria growth model via Laplace residual power series method, International Journal of Dynamics and Control, 2023, 11(2), 520-527. [42] M. N. Oqielat, T. Eriqat, Z. Al-Zhour, A. El-Ajou and S. Momani, Numerical solutions of time-fractional nonlinear water wave partial differential equation via Caputo fractional derivative: An effective analytical method and some applications, Applied and Computational Mathematics, 2022, 21(2), 207-222. [43] K. M. Owolabi and A. Atangana, Chaotic behaviour in system of noninteger-order ordinary differential equations, Chaos, Solitons and Fractals, 2018, 115, 362-370. [44] P. Rahimkhani, Y. Ordokhani and E. Babolian, Numerical solution of fractional pantograph differential equations by using generalized fractional-order Bernoulli wavelet, Journal of Computational and Applied Mathematics, 2017, 309, 493-510. [45] M. M. Al-Sawalha, A. Khan, O. Y. Ababneh and T. Botmart, Fractional view analysis of Kersten-Krasil'shchik coupled KdV-mKdV systems with non-singular kernel derivatives, AIMS Math., 2022, 7(10), 18334-18359. [46] A. K. H. Sedeeg, A coupling Elzaki transform and homotopy perturbation method for solving nonlinear fractional heat-like equations, Am. J. Math. Comput. Model, 2016, 1, 15-20. [47] R. Shah, Y. Alkhezi and K. Alhamad, An analytical approach to solve the fractional Benney equation using the q-homotopy analysis transform method, Symmetry, 2023, 15(3), 669. [48] A. P. Shakir, T. A. Sulaiman, H. F. Ismael, N. A. Shah and S. M. Eldin, Multiple fusion solutions and other waves behavior to the Broer-Kaup-Kupershmidt system, Alexandria Engineering Journal, 2023, 74, 559-567. [49] J. Shi, C. Liu and J. Liu, Hypergraph-based model for modeling multi-agent q-learning dynamics in public goods games, IEEE Transactions on Network Science and Engineering, 2024, 11(6), 6169-6179. DOI: 10.1109/TNSE.2024.3473941. [50] Q. Shi, S. Wang and J. Yang, Small parameters analysis applied to two potential issues for Maxwell-Schrödinger system, Journal of Differential Equations, 2025, 424, 637-659. DOI: 10.1016/j.jde.2025.01.049. [51] M. Suleman, T. Elzaki, Q. Wu, N. Anjum and J. U. Rahman, New application of Elzaki projected differential transform method, Journal of Computational and Theoretical Nanoscience, 2017, 14(1), 631-639. [52] P. Sunthrayuth, A. M. Zidan, S. W. Yao and M. Inc, The comparative study for solving fractional-order Fornberg-Whitham equation via $\rho$-Laplace transform, Symmetry, 2021, 13(5), 784. [53] H. Wang, Y. Hou, Y. He, C. Wen, B. Giron-Palomares, Y. Duan and Y. Wang, A physical-constrained decomposition method of infrared thermography: Pseudo restored heat flux approach based on ensemble bayesian variance tensor fraction, IEEE Transactions on Industrial Informatics, 2024, 20(3), 3413-3424. DOI: 10.1109/TII.2023.3293863. [54] K. J. Wang and K. L. Wang, Variational principles for fractal Whitham-Broer-Kaup equations in shallow water, Fractals, 2021, 29(02), 2150028. [55] Y. Xiao, Y. Yang, D. Ye and J. Zhang, Quantitative Precision Second-Order Temporal Transformation Based Pose Control for Spacecraft Proximity Operations, IEEE Transactions on Aerospace and Electronic Systems, 2024. [56] H. Yang, Q. Feng, X. Wang, D. Urynbassarova and A. A. Teali, Reduced biquaternion windowed linear canonical transform: Properties and applications, Mathematics, 2024, 12(5), 743. DOI: 10.3390/math12050743. [57] H. Yasmin, A. S. Alshehry, A. H. Ganie, A. Shafee and R. Shah, Noise effect on soliton phenomena in fractional stochastic Kraenkel-Manna-Merle system arising in ferromagnetic materials, Scientific Reports, 2024, 14(1), 1810. [58] H. H. Zhang, Z. H. Fan and R. S. Chen, Incomplete LU factorization preconditioner for the efficient solution of improved electric field integral equations, in 2010 International Conference on Microwave and Millimeter Wave Technology, IEEE, 2010, 599-602. [59] H. H. Zhang, Z. H. Fan and R. S. Chen, Marching-on-in-degree solver of time-domain finite element-boundary integral method for transient electromagnetic analysis, IEEE Transactions on Antennas and Propagation, 2013, 62(1), 319-326. [60] H. H. Zhang, H. M. Yao and L. J. Jiang, Novel time domain integral equation method hybridized with the macromodels of circuits, in 2015 IEEE 24th Electrical Performance of Electronic Packaging and Systems (EPEPS), IEEE, 2015 135-138. [61] S. Zhang, Y. Yang and H. Yang, A meshless symplectic algorithm for nonlinear wave equation using highly accurate RBFs quasi-interpolation, Applied Mathematics and Computation, 2017, 314, 110-120. [62] Z. Zhang, M. Lin, D. Li, R. Wu, R. Lin and C. Yang, An AUV-Enabled Dockable Platform for Long-Term Dynamic and Static Monitoring of Marine Pastures, IEEE Journal of Oceanic Engineering, 2024. [63] Y. Zhou and L. Peng, On the time-fractional Navier-Stokes equations, Computers and Mathematics with Applications, 2017, 73(6), 874-891. -
-
Figures(8) / Tables(4)
Export File
Citation
Azzh Saad Alshehry, Saima Noor, Abdulkafi Mohammed Saeed, Ahmad Shafee, Rasool Shah. INNOVATIVE SOLUTIONS FOR FRACTIONAL WHITHAM-BROER-KAUP MODEL USING TRANSFORM-BASED METHODS[J]. Journal of Applied Analysis & Computation, 2025, 15(6): 3805-3825. doi: 10.11948/20250039
Format
Content
DownLoad:
-
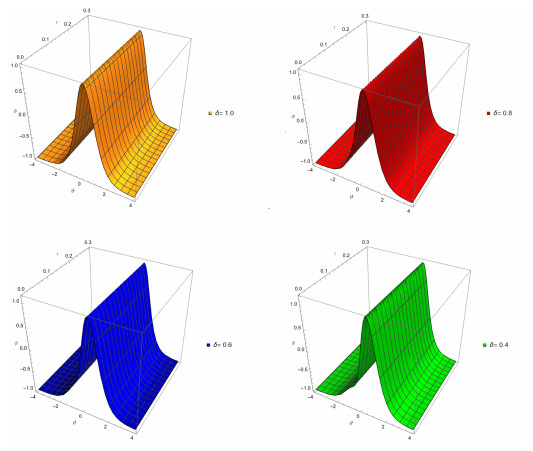
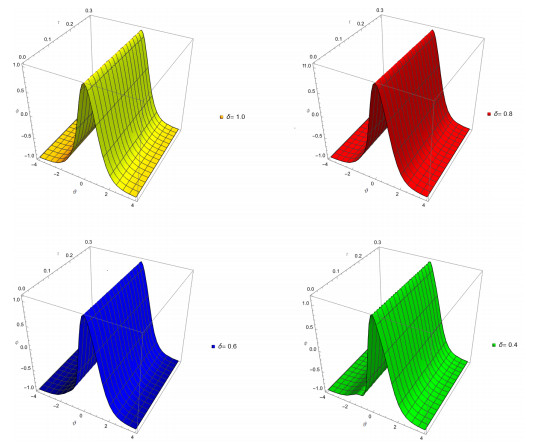
Figure 1.
In Figure 1, ERPSM solution for (a), (b), (c) and (d) shows that fractional order at
$ \delta=1 $ $ \delta=0.8 $ $ \delta=0.6 $ $ \delta=0.4 $ $ \tau=0.3 $ $ \varphi{(\vartheta,\tau)} $ -
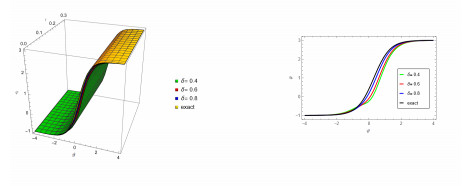
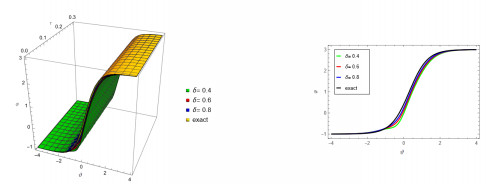
Figure 2.
In Figure 2, Comparison between ERPSM solution and exact for 3D plot of
$ \varphi{(\vartheta,\tau)} $ $ \tau=0.3 $ $ \delta=1 $ $ \delta=0.8 $ $ \delta=0.6 $ $ \delta=0.4 $ -
Figure 3.
In Figure 3, ERPSM solution for (a), (b), (c) and (d) shows that fractional order at
$ \delta=1 $ $ \delta=0.8 $ $ \delta=0.6 $ $ \delta=0.4 $ $ \tau=0.3 $ $ \phi{(\vartheta,\tau)} $ -
Figure 4.
In Figure 4, comparison between ERPSM solution and exact for 3D plot of
$ \phi{(\vartheta,\tau)} $ $ \tau=0.3 $ $ \delta=1 $ $ \delta=0.8 $ $ \delta=0.6 $ $ \delta=0.4 $ -
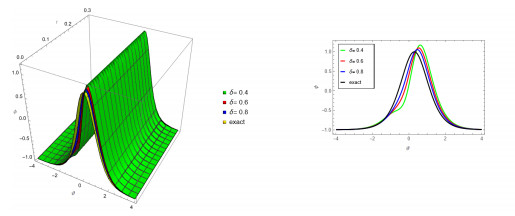
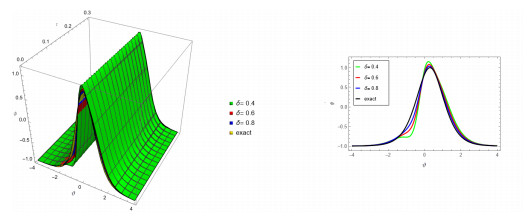
Figure 5.
In Figure 5, NITM solution for (a), (b), (c) and (d) shows that fractional order at
$ \delta=1 $ $ \delta=0.8 $ $ \delta=0.6 $ $ \delta=0.4 $ $ \tau=0.3 $ $ \varphi{(\vartheta,\tau)} $ -
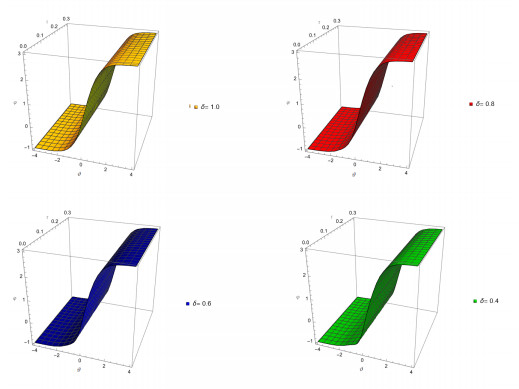
Figure 6.
In Figure 6, comparison between NITM solution and exact for 3D plot of
$ \varphi{(\vartheta,\tau)} $ $ \tau=0.3 $ $ \delta=1 $ $ \delta=0.8 $ $ \delta=0.6 $ $ \delta=0.4 $ -
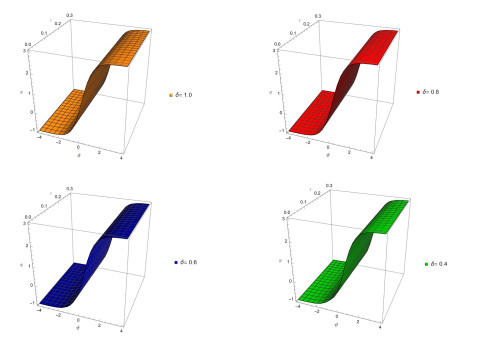
Figure 7.
In Figure 7, NITM solution for (a), (b), (c) and (d) shows that fractional order at
$ \delta=1 $ $ \delta=0.8 $ $ \delta=0.6 $ $ \delta=0.4 $ $ \tau=0.3 $ $ \phi{(\vartheta,\tau)} $ -
Figure 8.
In Figure 8, comparison between NITM solution and exact for 3D plot of
$ \phi{(\vartheta,\tau)} $ $ \tau=0.3 $ $ \delta=1 $ $ \delta=0.8 $ $ \delta=0.6 $ $ \delta=0.4 $