| Citation: | M. Elsaid Ramadan, Hamdy M. Ahmed, Abeer S. Khalifa, Karim K. Ahmed. INVARIANT SOLITONS AND TRAVELLING-WAVE SOLUTIONS TO A HIGHER-ORDER NONLINEAR SCHRÖDINGER EQUATION IN AN OPTICAL FIBER WITH AN IMPROVED TANH-FUNCTION ALGORITHM[J]. Journal of Applied Analysis & Computation, 2025, 15(6): 3270-3289. doi: 10.11948/20250042 |
INVARIANT SOLITONS AND TRAVELLING-WAVE SOLUTIONS TO A HIGHER-ORDER NONLINEAR SCHRÖDINGER EQUATION IN AN OPTICAL FIBER WITH AN IMPROVED TANH-FUNCTION ALGORITHM
-
Abstract
Optical fiber connection is essential to modern communication. A high-order nonlinear Schrödinger equation (NLSE) with additional dispersion of high-order and nonlinear components is studied in an inhomogeneous optical fiber. We provide numerous new analytic solutions via the improved modified extended tanh-function algorithm, including rational solution, singular periodic solution, Jacobi elliptic solutions (JESs), (bright, singular, dark) soliton, Weierstrass elliptic doubly periodic type solutions, and exponential solution. By employing the previously outlined method, they demonstrate their uniqueness for the given challenge. The results are presented in a clear and concise manner for various values of the necessary free parameters. Wolfram Mathematica's contour plot and 2D and 3D visualisations are used to show this process. The outcomes show how accurate, knowledgeable, and effective the computational procedures were. They may be used for increasingly complicated phenomena by integrating them with representational calculations. This finding constitutes a major advancement in our comprehension of the intricate and capricious behavior of this mathematical model.
-
Keywords:
- Higher-order NLSE /
- inhomogeneous optical fiber /
- solitons /
- powerful analytic method
-

-
References
[1] K. K. Ahmed, H. M. Ahmed, N. M. Badra and W. B. Rabie, Optical solitons retrieval for an extension of novel dual-mode of a dispersive non-linear Schrödinger equation, Optik, 2024, 307, 171835. doi: 10.1016/j.ijleo.2024.171835 [2] K. K. Ahmed, N. M. Badra, H. M. Ahmed and W. B. Rabie, Soliton solutions and other solutions for Kundu-Eckhaus equation with quintic nonlinearity and Raman effect using the improved modified extended tanh-function method, Mathematics, 2022, 10(22), 4203. doi: 10.3390/math10224203 [3] K. K. Ahmed, N. M. Badra, H. M. Ahmed and W. B. Rabie, Soliton solutions of generalized Kundu-Eckhaus equation with an extra-dispersion via improved modified extended tanh-function technique, Opt. Quantum Electron., 2023, 55(4), 299. doi: 10.1007/s11082-023-04599-x [4] K. K. Ahmed, N. M. Badra, H. M. Ahmed, W. B. Rabie, M. Mirzazadeh, M. Eslami and M. S. Hashemi, Investigation of solitons in magneto-optic waveguides with Kudryashov's law nonlinear refractive index for coupled system of generalized nonlinear Schrödinger's equations using modified extended mapping method, Nonlinear Anal-Model, 2024, 1-19. [5] K. K. Ahmed, H. H. Hussein, H. M. Ahmed, W. B. Rabie and W. Alexan, Analysis of the dynamical behaviors for the generalized Bogoyavlvensky-Konopelchenko equation and its analytical solutions occurring in mathematical physics, Ain Shams Eng. J., 2024, 15(11), 103000. doi: 10.1016/j.asej.2024.103000 [6] N. H. Ali, S. A. Mohammed and J. Manafian, Study on the simplified MCH equation and the combined KdV-mKdV equations with solitary wave solutions, Partial Differ. Equ. Appl. Math., 2024, 9, 100599. doi: 10.1016/j.padiff.2023.100599 [7] C. L. Bai and H. Zhao, Generalized extended tanh-function method and its application, Chaos, Solitons Fract., 2006, 27(4), 1026-1035. doi: 10.1016/j.chaos.2005.04.069 [8] I. Bendahmane, H. Triki, A. Biswas, A. S. Alshomrani, Q. Zhou, S. P. Moshokoa and M. Belic, Bright, dark and W-shaped solitons with extended nonlinear Schrödinger's equation for odd and even higher-order terms, Superlattice. Microst., 2018, 114, 53-61. doi: 10.1016/j.spmi.2017.12.007 [9] S. Boscolo and C. Finot, Artificial neural networks for nonlinear pulse shaping in optical fibers, Opt. Laser Techol., 2020, 131, 106439. doi: 10.1016/j.optlastec.2020.106439 [10] B. Cao and H. Zhang, Conversions and interactions of the nonlinear waves in a generalized higher-order nonlinear Schrödinger equation, Optik, 2018, 158, 112-117. doi: 10.1016/j.ijleo.2017.11.195 [11] J. Chen, Z. Luan, Q. Zhou, A. K. Alzahrani, A. Biswas and W. Liu, Periodic soliton interactions for higher-order nonlinear Schrödinger equation in optical fibers, Nonlinear Dyn., 2020, 100, 2817-2821. doi: 10.1007/s11071-020-05649-9 [12] S. Chettouh, H. Triki, A. El-Akrmi, Q. Zhou, S. P. Moshokoa, M. Z. Ullah, A. Biswas and M. Belic, Dipole solitons in an extended nonlinear Schrödinger's equation with higher-order even and odd terms, Optik, 2017, 145, 644-649. doi: 10.1016/j.ijleo.2017.08.034 [13] C. H. Feng, B. Tian and X. T. Gao, Bilinear form, N solitons, breathers and periodic waves for a (3+1)-dimensional Korteweg-de Vries equation with the time-dependent coefficients in a fluid, Qual. Theory Dyn. Syst., 2024, 23(1), 291. [14] C. Finot and S. Boscolo, Nonlinear shaping of light in optical fibers, Adv. Nonlin. Photon., 2023, 381-412. [15] X. Y. Gao, In an ocean or a river: Bilinear auto-Bäcklund transformations and similarity reductions on an extended time-dependent (3+1)-dimensional shallow water wave equation, China Ocean Eng., 2025, 39, 160-165. doi: 10.1007/s13344-025-0012-y [16] X. Y. Gao, Hetero-Bäcklund transformation, bilinear forms and multi-solitons for a (2+1)-dimensional generalized modified dispersive water-wave system for the shallow water, Chin. J. Phys., 2024, 92, 1233-1239. doi: 10.1016/j.cjph.2024.10.004 [17] X. Y. Gao, Symbolic computation on a (2+1)-dimensional generalized nonlinear evolution system in fluid dynamics, plasma physics, nonlinear optics and quantum mechanics, Qual. Theory Dyn. Syst., 2024, 23(5), 202. doi: 10.1007/s12346-024-01045-5 [18] X. Y. Gao, In plasma physics and fluid dynamics: Symbolic computation on a (2+1)-dimensional variable-coefficient Sawada-Kotera system, Appl. Math. Lett., 2025, 159, 109262. doi: 10.1016/j.aml.2024.109262 [19] X. Y. Gao, Oceanic shallow-water investigations on a generalized Whitham-Broer-Kaup-Boussinesq-Kupershmidt system, Phys. Fluids, 2023, 35(12), 127106. doi: 10.1063/5.0170506 [20] X. Y. Gao, Two-layer-liquid and lattice considerations through a (3+1)-dimensional generalized Yu-Toda-Sasa-Fukuyama system, Appl. Math. Lett., 2024, 152, 109018. doi: 10.1016/j.aml.2024.109018 [21] X. T. Gao and B. Tian, Similarity reductions on a (2+1)-dimensional variable-coefficient modified Kadomtsev-Petviashvili system describing certain electromagnetic waves in a thin film, Int. J. Theor. Phys., 2024, 63(4), 99. doi: 10.1007/s10773-024-05629-4 [22] W. Y. Guan and B. Q. Li, New observation on the breather for a generalized nonlinear Schrödinger system with two higher-order dispersion operators in inhomogeneous optical fiber, Optik, 2019, 181, 853-861. doi: 10.1016/j.ijleo.2018.12.148 [23] N. Gupta, A. K. Alex, R. Partap and R. Johari, Self action effects of q-Gaussian laser beam in preformed parabolic plasma channels: Effect of nonlinear absorption, J. Opt., 2024, 1-14. [24] K. Hammani, B. Kibler, J. Fatome, S. Boscolo, G. Genty, J. M. Dudley, G. Millot and C. Finot, Nonlinear spectral shaping and optical rogue events in fiber-based systems, Opt. Fiber. Technol., 2012, 18, 248-256. doi: 10.1016/j.yofte.2012.06.009 [25] H. H. Hussein, H. M. Ahmed, W. B. Rabie, K. K. Ahmed, M. S. Hashemi and M. Bayram, Multiple soliton solutions and other travelling wave solutions to new structured (2+1)-dimensional integro-partial differential equation using efficient technique, Phys. Scr., 2024, 99(10), 105270. doi: 10.1088/1402-4896/ad7993 [26] Y. Jiang, B. Tian, W. -J. Liu, K. Sun, M. Li and P. Wang, Soliton interactions and complexes for coupled nonlinear Schrödinger equations, Phys. Rev. E, 2012, 85(3), 036605. doi: 10.1103/PhysRevE.85.036605 [27] E. Kengne, Engineering of chirp localized waves in optical media with positive group velocity dispersion, Chaos Solitons Fract., 2024, 187, 115354. doi: 10.1016/j.chaos.2024.115354 [28] A. S. Khalifa, H. M. Ahmed, N. M. Badra and W. B. Rabie, Exploring solitons in optical twin-core couplers with Kerr law of nonlinear refractive index using the modified extended direct algebraic method, Opt. Quantum Electron., 2024, 56(6), 1060. doi: 10.1007/s11082-024-06882-x [29] A. S. Khalifa, N. M. Badra, H. M. Ahmed and W. B. Rabie, Retrieval of optical solitons in fiber Bragg gratings for high-order coupled system with arbitrary refractive index, Optik, 2023, 287, 171116. doi: 10.1016/j.ijleo.2023.171116 [30] Y. Kuang and L. Tian, Higher-order soliton solutions for the derivative nonlinear Schrödinger equation via improved Riemann-Hilbert method, J. Nonlinear Math. Phys., 2024, 31, 58. doi: 10.1007/s44198-024-00228-7 [31] Z. Z. Lan, Multi-soliton solutions, breather-like and bound-state solitons for complex modified Korteweg-de Vries equation in optical fibers, Chin. Phys. B, 2024, 33(6), 060201. doi: 10.1088/1674-1056/ad39d7 [32] Z. Z. Lan, N-soliton solutions, Bäcklund transformation and Lax Pair for a generalized variable-coefficient cylindrical Kadomtsev-Petviashvili equation, Appl. Math. Lett., 2024, 158, 109239. doi: 10.1016/j.aml.2024.109239 [33] Z. Z. Lan, Multiple soliton asymptotics in a spin-1 Bose-Einstein condensate, Chin. Phys. Lett., 2024, 41(9), 090501. doi: 10.1088/0256-307X/41/9/090501 [34] Z. Z. Lan, Semirational rogue waves of the three coupled higher-order nonlinear Schrödinger equations, Appl. Math. Lett., 2024, 147, 108845. doi: 10.1016/j.aml.2023.108845 [35] Z. Z. Lan, Bound-state solitons in three-wave resonant interactions, Nonlinear Dyn., 2024, 112(22), 20173-20181. doi: 10.1007/s11071-024-10121-z [36] J. Li, C. Wang and P. Wang, Narrow-bandwidth picosecond dissipative soliton resonance in an all-anomalous-dispersion Er/Yb co-doped fiber laser, Opt. Fiber. Technol., 2024, 82, 103637. doi: 10.1016/j.yofte.2023.103637 [37] F. Y. Liu, Y. T. Gao, X. Yu and C. C. Ding, Wronslian, Gramian, Pfaffian and periodic-wave solutions for a (3+1)-dimensional generalized nonlinear evolution equation arising in the shallow water waves, Nonlinear Dynam., 2022, 108, 1599-1616. doi: 10.1007/s11071-022-07249-1 [38] S. S. Mahmood and M. A. S. Murad, Soliton solutions to time-fractional nonlinear Schrödinger equation with cubic-quintic-septimal in weakly nonlocal media, Phys. Lett. A., 2024, 130183. [39] M. A. S. Murad, H. F. Ismael, T. A. Sulaiman and H. Bulut, Analysis of optical solutions of higher-order nonlinear Schrödinger equation by the new Kudryashov and Bernoulli's equation approaches, Opt. Quantum Electron., 2024, 56(1), 76. doi: 10.1007/s11082-023-05612-z [40] W. B. Rabie, K. K. Ahmed, N. M. Badra, H. M. Ahmed, M. Mirzazadeh and M. Eslami, New solitons and other exact wave solutions for coupled system of perturbed highly dispersive CGLE in birefringent fibers with polynomial nonlinearity law, Opt. Quantum Electron., 2024, 56(5), 1-22. [41] H. W. Shan, B. Tian, C. D. Cheng, X. T. Gao, Y. Q. Chen and H. D. Liu, N-soliton and other analytic solutions for a (3+1)-dimensional Korteweg-de Vries-Calogero-Bogoyavlenskii-Schiff equation with the time-dependent coefficients for the shallow water waves, Qual. Theory Dyn. Syst., 2024, 23(Suppl 1), 267. [42] E. Tego, F. Matera and D. D. Buono, Experimental investigation on transmission control protocol throughput behavior in optical fiber access networks, Fiber Integr. Opt., 2016, 35, 72-85. doi: 10.1080/01468030.2016.1153172 [43] H. Triki, A. Biswas, D. Milovi'c and M. Beli'c, Chirped optical solitons in birefringent fibers with parabolic law nonlinearity and four-wave mixing, Acta Phys. Pol. A, 2016, 130(3), 718-726. doi: 10.12693/APhysPolA.130.718 [44] C. C. Wei, B. Tian, D. Y. Yang and S. H. Liu, Jacobian-elliptic-function and rogue-periodic-wave solutions of a high-order nonlinear Schrödinger equation in an inhomogeneous optical fiber, Chin. J. Phys., 2023, 81, 354-361. [45] X. H. Wu, Y. T. Gao and X. Yu, Dark-soliton asymptotics for a repulsive nonlinear system in a baroclinic flow, Phys. Fluids, 2024, 36(5), 056615. [46] X. H. Wu, Y. T. Gao, X. Yu, C. C. Ding and L. Q. Li, Modified generalized Darboux transformation and solitons for a Lakshmanan-Porsezian-Daniel equation, Chaos Solitons Fract., 2022, 162, 112399. [47] H. M. Yin, Q. Pan and K. W. Chow, The Fermi-Pasta-Ulam-Tsingou recurrence for discrete systems: Cascading mechanism and machine learning for the Ablowitz-Ladik equation, Commun. Nonlinear Sci. Numer. Simul., 2022, 114, 106664. [48] X. H. Zhao, Multi-solitons and integrability for a (2+1)-dimensional variable coefficients Date-Jimbo-Kashiwara-Miwa equation, Appl. Math. Lett., 2024, 149, 108895. [49] X. H. Zhao and S. X. Li, Dark soliton solutions for a variable coefficient higher-order Schrödinger equation in the dispersion decreasing fibers, Appl. Math. Lett., 2022, 132, 108159. [50] Q. Zhou, Q. Zhu and A. Biswas, Optical solitons in birefringent fibers with parabolic law nonlinearity, Opt. Appl., 2014, 44(3), 399-409. -
-
-
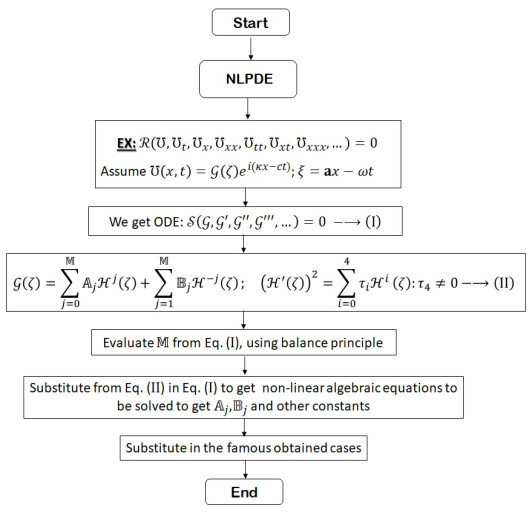
Figure 1.
A flow chart of the IMETFA steps.
-
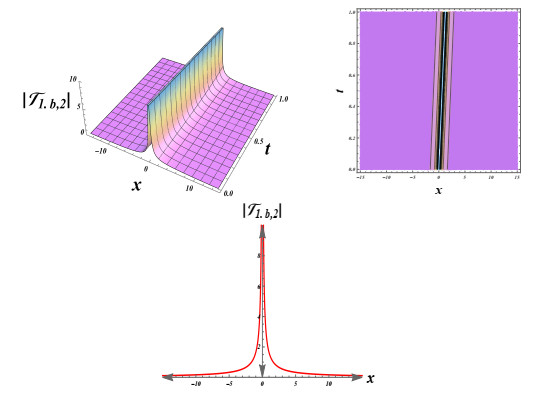
Figure 2.
Bright soliton solution simulations of Eq. (4.7).
-
Figure 3.
Singular periodic solution simulations of Eq. (4.8).
-
Figure 4.
Rational solution simulations of Eq. (4.9).
-
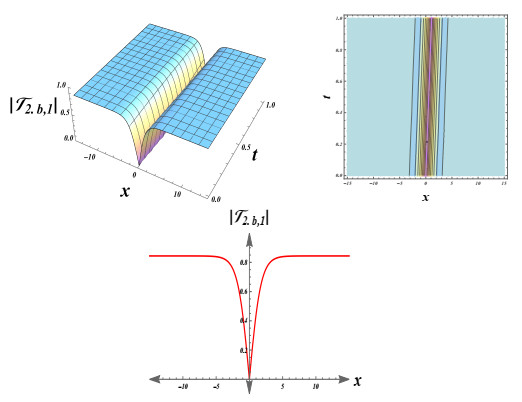
Figure 5.
Dark soliton solution simulations of Eq. (4.14).
-
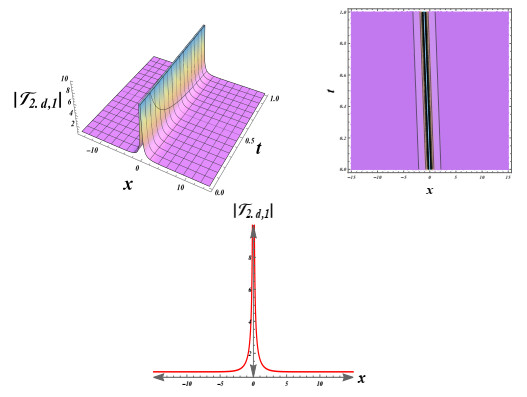
Figure 6.
Singular soliton solution simulations of Eq. (4.21).




 DownLoad:
DownLoad: