| Citation: | Li Wang, Xiaomei Liu, Kun-Peng Jin. COMPARISON OF RIEMANN SOLUTIONS TO THE EULER EQUATIONS FOR MODIFIED AND GENERALIZED CHAPLYGIN GAS DYNAMICS[J]. Journal of Applied Analysis & Computation, 2025, 15(6): 3290-3316. doi: 10.11948/20240534 |
COMPARISON OF RIEMANN SOLUTIONS TO THE EULER EQUATIONS FOR MODIFIED AND GENERALIZED CHAPLYGIN GAS DYNAMICS
-
Abstract
In this article, utilizing the method of characteristic analysis, we construct the Riemann solutions of the Euler equations for the modified and the generalized Chaplygin gas, which contains rarefaction waves, shock waves, contact discontinuities and $ \delta- $ shock waves. For the $ \delta- $ shock waves, we propose generalized Rankine-Hugoniot relation and entropy conditon. Moreover, by studing the limiting behaviour, we find that the Riemann solutions of modified Chaplygin gas is the same as generalized Chaplygin gas including the $ \delta- $shock waves. Moreover, we give some numerical simulations to verify the theoretical analysis.
-

-
References
[1] M. C. Bento, O. Bertolami and A. A. Sen, Generalized Chaplygin gas model: Dark energy-dark matter unification and cmbrconstraints, Gen. Relativ. Gravit, 2003, 35, 2063–2069. doi: 10.1023/A:1026207312105 [2] N. Bilic, G. B. Tupper and R. Viollier, Dark matter, dark energy and the Chaplygin gas, Dark Matter in Astro- and Particle Physics, 2002, 306–311. DOI: 10.1007/978-3-642-55739-2-30. [3] Y. Brenier, Solutions with concentration to the Riemann problem for the one-dimensional Chaplygin gas equations, J. Math. Fluid Mech., 2005, 7, 326–331. doi: 10.1007/s00021-005-0162-x [4] S. Chaplygin, On gas jets, Sci. Mem. Mosc. Univ. Math. Phys., 1904, 21, 1–121. [5] R. K. Chaturvedi, L. P. Singh and D. Zeidan, Delta shock wave solution of the Riemann problem for the non-homogeneous modified Chaplygin gasdynamics, Journal of Dynamics and Differential Equations, 2022, 34(2), 1067–1084. doi: 10.1007/s10884-020-09914-8 [6] H. J. Cheng and H. C. Yang, Riemann problem for the relativistic Chaplygin Euler equations, J. Math. Anal. Appl., 2011, 381, 17–26. doi: 10.1016/j.jmaa.2011.04.017 [7] Q. Ding and L. Guo, The vanishing pressure limit of Riemann solutions to the non-isentropic Euler equations for generalized Chaplygin gas, Adv. Math. Phys., 2019, 5253717. [8] V. Gorini, A. Kamenshchik, U. Moschella and V. Pasquier, The Chaplygin gas as a model for dark energy, The Tenth Marcel Grossmann Meeting, 2006. DOI: 10.1142/9789812704030-0050. [9] L. H. Guo, W. C. Sheng and T. Zhang, The two-dimensional Riemann problem for isentropic Chaplygin gas dynamic system, Commun. Pure Appl. Anal., 2010, 9(2), 431–458. doi: 10.3934/cpaa.2010.9.431 [10] W. F. Jiang, T. Li, Z. Wang and S. T. Fang, The limiting behavior of the Riemann solutions of non-isentropic modified Chaplygin gas dynamics, J. Math. Phys., 2021, 62, 041501. doi: 10.1063/5.0033806 [11] W. F. Jiang, T. Li, Z. Wang and T. T. Zhang, The Riemann solutions comparison for compressible Euler equations in different Chaplygin gas states, Applicable Analysis, 2022, 101(3), 4759–4773. [12] D. X. Kong and C. Wei, Formation and propagation of singularities in one-dimensional Chaplygin gas, J. Geom. Phys., 2014, 80, 58–70. doi: 10.1016/j.geomphys.2014.02.009 [13] A. Kumar and R. Radha, Riemann problem for the Chaplygin gas equations for several classes of non-constant initial data, European Journal of Mechanics B-Fluids, 2022, 91, 121–127. doi: 10.1016/j.euromechflu.2021.09.013 [14] Z. T. Lei and Z. Q. Shao, The limit behavior of Riemann solutions to the Euler equations of compressible fluid flow for the modified Chaplygin gas, Journal of Mathematical Physics, 2022, 63(7). DOI: 10.1063/5.0090251. [15] H. H. Li and Z. Q. Shao, Delta shocks and vacuum states in vanishing pressure limits of solutions to the relativistic Euler equations for generalized Chaplygin gas, Commun. Pure Appl. Anal., 2016, 15(6), 2373–2400. doi: 10.3934/cpaa.2016041 [16] Y. Pang, Delta shock wave with Dirac delta function in multiple components for the system of generalized Chaplygin gas dynamics, Boundary Value Probl., 2016(1). DOI: 10.1186/s13661-016-0712-6. [17] Y. Pang, Delta shock wave in the compressible Euler equations for a Chaplygin gas, J. Math. Anal. Appl., 2017, 448, 245–261. doi: 10.1016/j.jmaa.2016.10.078 [18] Priyanka and M. Zafar, Delta shocks and vacuum states in the Riemann solutions of Chaplygin Euler equations as pressure and magnetic field drop to zero, Journal of Mathematical Physics, 2022. DOI: 10.1063/5.0132580. [19] A. F. Qu and L. Wang, Dependence of perturbation on the limit of Riemann solutions in non-isentropic Chaplygin gas dynamics, Chin. Ann. Math., Ser. A, 2018, 39(2), 219–228. [20] A. F. Qu and Z. Wang, Stability of the Riemann solutions for a Chaplygin gas, J. Math. Anal. Appl., 2014, 409(1), 347–361. doi: 10.1016/j.jmaa.2013.07.018 [21] D. Serre, Multidimensional shock interaction for a Chaplygin gas, Arch Rational Mech Anal, 2009, 191, 539–577. doi: 10.1007/s00205-008-0110-z [22] M. R. Setare, Holographic Chaplygin gas model, Phys Lett B, 2007, 648, 329–332. doi: 10.1016/j.physletb.2007.03.025 [23] W. C. Sheng, G. J. Wang and G. Yin, Delta wave and vacuum state for generalized Chaplygin gas dynamics system as pressure vanishes, Nonlinear Analysis: Real World Applications, 2015, 22, 115–128. doi: 10.1016/j.nonrwa.2014.08.007 [24] M. Singh and R. Arora, Generalized Riemann problem for the one-dimensional Chaplygin gas with a friction term, International Journal of Non-Linear Mechanics, 2023, 148. DOI: 10.1016/j.ijnonlinmec.2022.104298. [25] Y. Song and L. Guo, General limiting behavior of Riemann solutions to the non-isentropic Euler equations for modified Chaplygin gas, J. Math. Phys., 2020, 61(4), 041506. doi: 10.1063/1.5144326 [26] M. Tong, C. Shen and X. Lin, The asymptotic limits of Riemann solutions for the isentropic extended Chaplygin gas dynamic system with the vanishing pressure, Boundary Value Problems, 2018(1). DOI: 10.1186/s13661-018-1064-1. [27] H. S. Tsien, Two dimensional subsonic flow of compressible fluids, J Aeron Sci, 1939, 6, 399-–407. [28] G. D. Wang, The Riemann problem for one dimensional generalized Chaplygin gas dynamics, J. Math. Anal. Appl., 2013, 403(2), 434–450. [29] Z. Wang and Q. L. Zhang, The Riemann problem with delta initial data for the one-dimensional Chaplygin gas equations, Acta Math. Sci., 2012, 32(3), 825–841. [30] H. Yang and J. Wang, Delta-shocks and vacuum states in the vanishing pressure limit of solutions to the isentropic Euler equations for modified Chaplygin gas, J. Math. Anal. Appl., 2014, 413(2), 800–820. [31] J. Y. Zhu, M. X. Huang and Z. Q. Shao, The limiting behavior of Riemann solutions to the Euler equations of compressible fluid flow for the modified Chaplygin gas with the body force, Physics of Fluids, 2024, 36(2). DOI: 10.1063/5.0185216. [32] L. Zhu and W. C. Sheng, The Riemann problem of adiabatic Chaplygin gas dynamic system, Commun. Appl. Math. Comput., 2010, 24 (1), 9–16. -
-
-
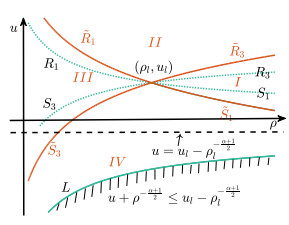
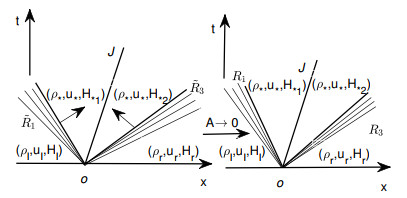
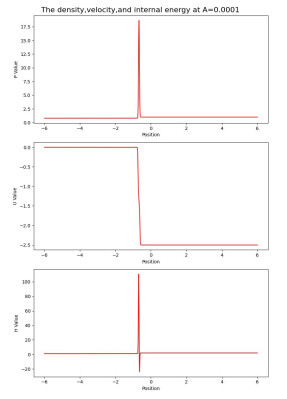
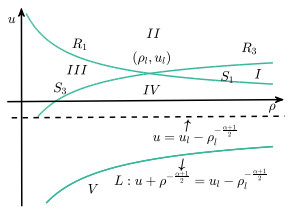
Figure 1.
Figure 1
-
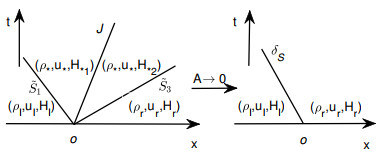
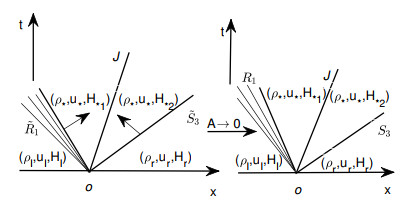
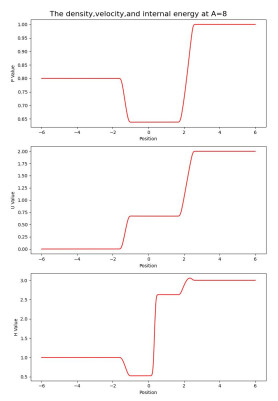
Figure 2.
Figure 2
-
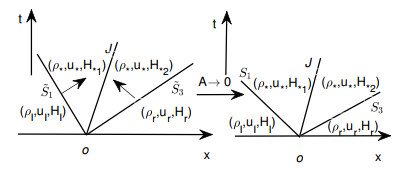
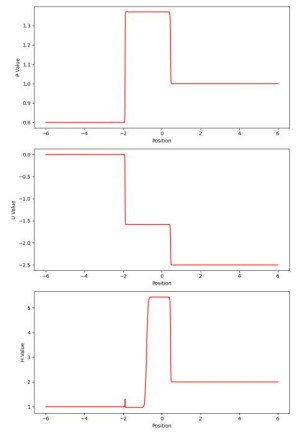
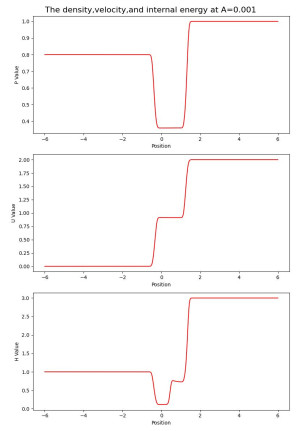
Figure 3.
Figure 3
-
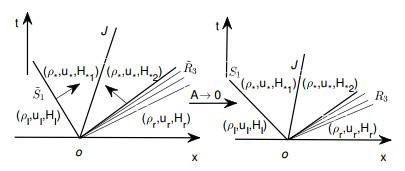
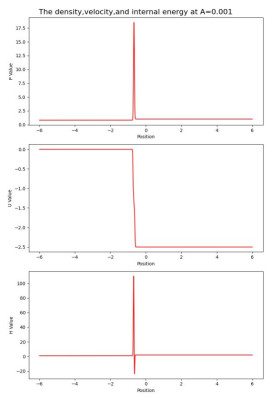
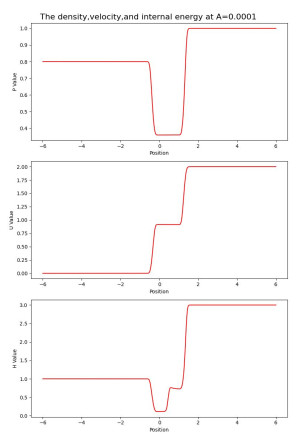
Figure 4.
Figure 4
-
Figure 5.
Figure 5
-
Figure 6.
Figure 6
-
Figure 7.
Figure 7
-
Figure 8.
Figure 8
-
Figure 9.
Figure 9
-
Figure 10.
Figure 10
-
Figure 11.
Figure 11
-
Figure 12.
Figure 12
-
Figure 13.
Figure 13




 DownLoad:
DownLoad: