| Citation: | Nazek A. Obeidat, Mahmoud S. Rawashdeh, Laith M. Khaleel. THEORIES AND APPLICATIONS OF ADOMIAN DECOMPOSITION $ \mathcal{J} $-TRANSFORM METHOD WITH THEORETICAL ANALYSIS AND SIMULATION[J]. Journal of Applied Analysis & Computation, 2025, 15(6): 3728-3750. doi: 10.11948/20250053 |
THEORIES AND APPLICATIONS OF ADOMIAN DECOMPOSITION $ \mathcal{J} $-TRANSFORM METHOD WITH THEORETICAL ANALYSIS AND SIMULATION
-
Abstract
This work focuses on using the Adomian decomposition $ \mathcal{J} $-transform method ($ \mathcal{ADJM} $) to solve both linear and nonlinear differential equations, with the aim of obtaining exact solutions for various types of differential equations, such as the Bratu equations and second-order linear partial telegraph equation. We present comprehensive proofs for new theorems associated with the $ \mathcal{J} $-transform method. This approach combines the $ \mathcal{J} $-transform method ($ \mathcal{JTM} $) and the Adomian decomposition method ($ \mathcal{ADM} $). We carry out a theoretical analysis of $ \mathcal{ADJM} $ applied to certain nonlinear differential equations and give proofs to the existence and uniqueness theorems along with error estimates. The solutions obtained are compared with exact solutions from other established methods in the literature. The study emphasizes the notable advantages of $ \mathcal{ADJM} $, highlighting its effectiveness in solving both ODEs and PDEs. In order to demonstrate the unique advantages of the employed method, we give exact solutions in the form of convergent power series with easily obtainable coefficients. Some of the symbolic and numerical calculations were executed using Mathematica software 13.
-

-
References
[1] M. J. Ablowitz and A. S. Fokas, Introduction to Complex Variables and Applications (Vol. 63), Cambridge University Press, 2021. [2] S. A. Ahmed, A. Qazza, R. Saadeh and T. M. Elzaki, Conformable double laplace-sumudu iterative method, Symmetry, 2022, 15(1), 78. doi: 10.3390/sym15010078 [3] M. O. Aibinu, F. M. Mahomed and P. E. Jorgensen, Solutions of fractional differential models by using Sumudu transform method and its hybrid, Partial Differential Equations in Applied Mathematics, 2024, 11, 100872. doi: 10.1016/j.padiff.2024.100872 [4] M. Almazmumy, A. A. Alsulami, H. O. Bakodah and N. A. Alzaid, Adomian decomposition method with inverse differential operator and orthogonal polynomials for nonlinear models, International Journal of Analysis and Applications, 2024, 22, 65-65. doi: 10.28924/2291-8639-22-2024-65 [5] S. Ali Alomari and Y. Qaid Hasan, Enhanced Adomian decomposition method for accurate numerical solutions of PDE, Asian Research Journal of Mathematics, 2024, 20(11), 26-41. doi: 10.9734/arjom/2024/v20i11857 [6] A. S. Alshehry, R. Shah, N. A. Shah and I. Dassios, A reliable technique for solving fractional partial differential equation, Axioms, 2022, 11(10), 574. doi: 10.3390/axioms11100574 [7] M. Ayalew, Numerical solution of time fractional Klein-Gordon equation in framework of the Yang-Abdel-Cattani fractional derivative operator, Advances in Analysis and Applied Mathematics, 2024, 1(2), 126-139. [8] C. Burgos, J. C. Cortés, L. Villafuerte and R. J. Villanueva, Solving random fractional second-order linear equations via the mean square Laplace transform: Theory and statistical computing, Applied Mathematics and Computation, 2022, 418, 126846. doi: 10.1016/j.amc.2021.126846 [9] A. T. Deresse, Analytical solution of one-dimensional nonlinear conformable fractional telegraph equation by reduced differential transform method, Advances in Mathematical Physics, 2022, 2022(1). DOI: 10.1155/2022/7192231. [10] H. M. Fahad, M. U. Rehman and A. Fernandez, On Laplace transforms with respect to functions and their applications to fractional differential equations, Mathematical Methods in the Applied Sciences, 2023, 46(7), 8304-8323. doi: 10.1002/mma.7772 [11] F. Haroon, S. Mukhtar and R. Shah, Fractional view analysis of Fornberg-Whitham equations by using Elzaki transform, Symmetry, 2022, 14(10), 2118. doi: 10.3390/sym14102118 [12] Q. Hou, Y. Li, V. P. Singh and Z. Sun, Physics-informed neural network for diffusive wave model, Journal of Hydrology, 2024, 637, 131261. doi: 10.1016/j.jhydrol.2024.131261 [13] H. Jin, S. Tian, J. Hu, L. Zhu and S. Zhang, Robust ratio-typed test for location change under strong mixing heavy-tailed time series model, Communications in Statistics-Theory and Methods, 2025, 1-24. [14] A. Keram and P. Huang, Convergence analysis of the Uzawa iterative method for the thermally coupled stationary in compressible magnetohydrodynamics flow, Journal of Applied Analysis & Computation, 2025, 15(3), 1563-1579. [15] E. Kuffi and S. F. Maktoof, "Emad-Falih transform" a new integral transform, Journal of Interdisciplinary Mathematics, 2021, 24(8), 2381-2390. doi: 10.1080/09720502.2021.1995194 [16] R. Kumar, J. Chandel and S. Aggarwal, A new integral transform "Rishi Transform" with application, Journal of Scientific Research, 2022, 14(2), 521-532. doi: 10.3329/jsr.v14i2.56545 [17] S. R. Kushare, D. P. Patil and A. M. Takate, The new integral transform, "Kushare transform", International Journal of Advances in Engineering and Management, 2021, 3(9), 1589-1592. [18] J. Liu, M. Nadeem and L. F. Iambor, Application of Yang homotopy perturbation transform approach for solving multi-dimensional diffusion problems with time-fractional derivatives, Scientific Reports, 2023, 13(1), 21855. doi: 10.1038/s41598-023-49029-w [19] S. Maitama and W. Zhao, Beyond Sumudu transform and natural transform: J-transform properties and applications, Journal of Applied Analysis and Computation, 2020, 10, 1223-1241. doi: 10.11948/20180258 [20] E. A. Mansour, E. A. Kuffi and S. A. Mehdi, The new integral transform "SEE transform" and its applications, Periodicals of Engineering and Natural sciences (PEN), 2021, 9(2), 1016-1029. doi: 10.21533/pen.v9i2.2023 [21] S. R. Moosavi Noori and N. Taghizadeh, Study of convergence of reduced differential transform method for different classes of differential equations, International Journal of Differential Equations, 2021, 2021(1). DOI: 10.1155/2021/6696414. [22] N. A. Obeidat and M. S. Rawashdeh, Theoretical analysis of new techniques applied to applications in fluid dynamics, International Journal of Modelling and Simulation, 2025, 45(2), 466-477. doi: 10.1080/02286203.2023.2216048 [23] N. A. Obeidat and M. S. Rawashdeh, On theories of natural decomposition method applied to system of nonlinear differential equations in fluid mechanics, Advances in Mechanical Engineering, 2023, 2023(1). DOI: 10.1177/16878132221149835. [24] N. A. Obeidat, M. S. Rawashdeh and R. Rababa'h, Important theories and applications arise in physics and engineering using a new technique: The natural decomposition method, Journal of Advanced Research in Applied Sciences and Engineering Technology, 2024, 34(1), 142-163. [25] N. A. Obeidat, M. S. Rawashdeh and M. N. Al Smadi, An efficient technique via the $\mathbb {J} $-transform decomposition method: Theoretical analysis with applications, Journal of Applied Analysis & Computation, 2025, 15(2), 1068-1090. [26] D. P. Patil and S. S. Khakale, The new integral transform "Soham transform", International Journal of Advances in Engineering and Managemen, 2021, 3(10), 126-132. [27] D. P. Patil, D. S. Patil and S. M. Kanchan, New integral transform, "Double Kushare transform", IRE Journals, 2022, 6(1), 45-52. [28] A. Qazza, A. Burqan, R. Saadeh and R. Khalil, Applications on double ARA-Sumudu transform in solving fractional partial differential equations, Symmetry, 2022, 14(9), 1817. doi: 10.3390/sym14091817 [29] A. Al-Rab'a, S. Al-Sharif and M. Al-Khaleel, Double conformable Sumudu transform, Symmetry, 2022, 14(11), 2249. doi: 10.3390/sym14112249 [30] M. S. Rawashdeh, N. A. Obeidat and H. S. Abedalqader, New class of nonlinear fractional integro-differential equations with theoretical analysis via fixed point approach: Numerical and exact solutions, Journal of Applied Analysis and Computation, 2023, 13(5), 2767-2787. doi: 10.11948/20220575 [31] N. Sharma, G. Alhawael, P. Goswami and S. Joshi, Variational iteration method for n-dimensional time-fractional Navier-Stokes equation, Applied Mathematics in Science and Engineering, 2024, 32(1). DOI: 10.1080/27690911.2024.2334387. [32] M. Shirazian, A new acceleration of variational iteration method for initial value problems, Mathematics and Computers in Simulation, 2023, 214, 246-259. [33] M. M. A. Taleb, S. A. A. Al-Salehi, S. Muhammad and V. C. Borkar, Fixed point theorems over B-metric-like spaces and applications in electric circuit equations, Journal of Applied Analysis & Computation, 2025, 15(3), 1430-1452. [34] Z. Wang, Y. Yang, F. Parastesh, S. Cao and J. Wang, Chaotic dynamics of a carbon nanotube oscillator with symmetry-breaking, Physica Scripta, 2024, 100(1), 015225. [35] Y. Yang and H. Li, Neural ordinary differential equations for robust parameter estimation in dynamic systems with physical priors, Applied Soft Computing, 2025, 169, 112649. doi: 10.1016/j.asoc.2024.112649 -
-
-
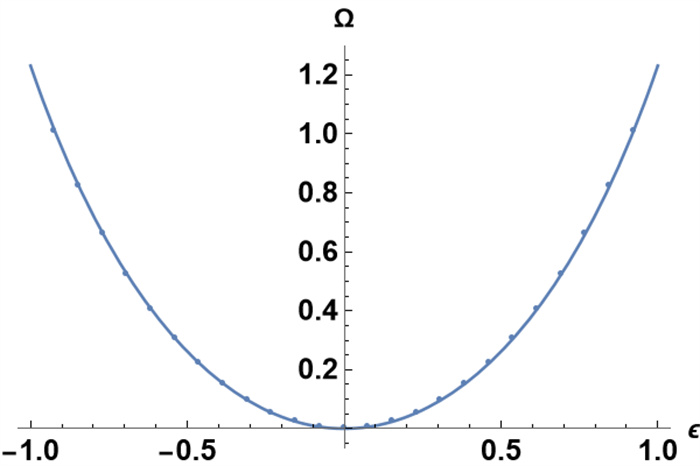
Figure 1.
Exact solution of
$ \Omega(\epsilon)$ -
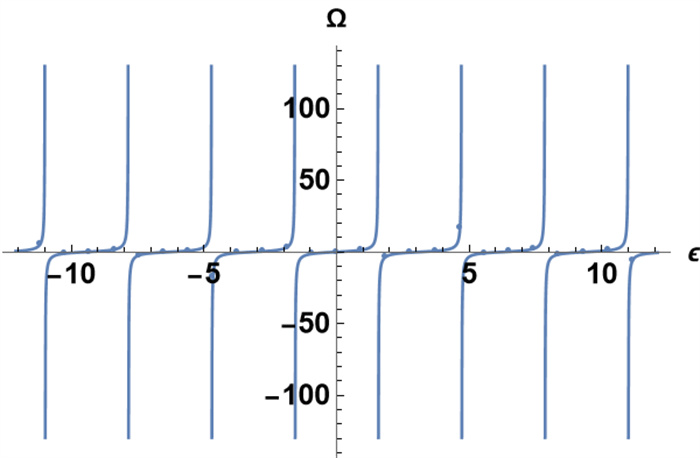
Figure 2.
Exact solution of
$ \Omega(\epsilon) $ -
Figure 3.
Exact solution of
$ \Omega(\epsilon)$ -
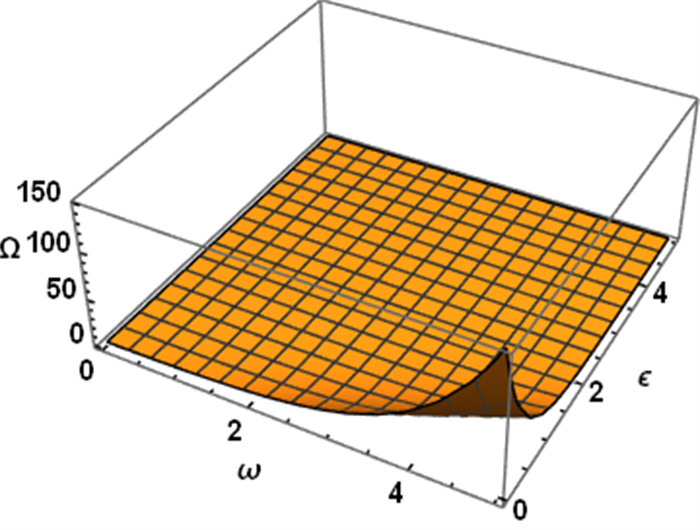
Figure 4.
Exact solution of
$ \Omega(\omega, \epsilon) $ -
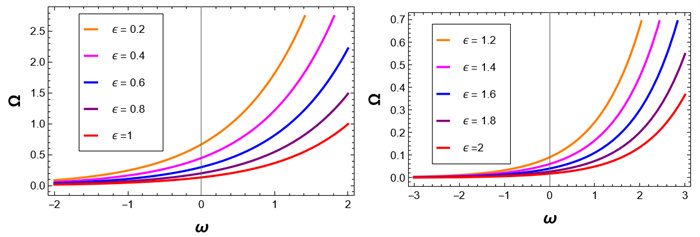
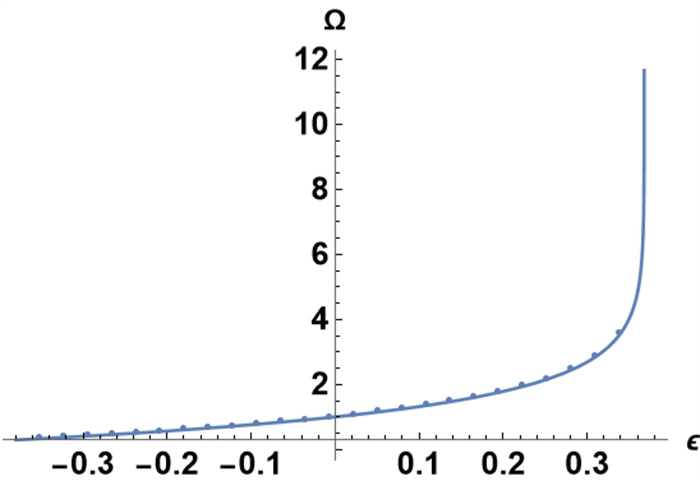
Figure 5.
Numerical solutions of
$ \Omega(\omega) $ $ \epsilon $




 DownLoad:
DownLoad: