| Citation: | Shuhao Wu, Xin Lu. DYNAMICS OF A DIFFUSIVE SINGLE-SPECIES MODEL WITH NONLOCALITY AND DISTRIBUTED MEMORY[J]. Journal of Applied Analysis & Computation, 2025, 15(6): 3751-3768. doi: 10.11948/20250093 |
DYNAMICS OF A DIFFUSIVE SINGLE-SPECIES MODEL WITH NONLOCALITY AND DISTRIBUTED MEMORY
-
Abstract
Cognitive abilities and memorized information are significant for "smart" animals to make movement decisions. This work establishes a diffusive single-species model with nonlocality and distributed memory. We consider weak and strong temporal kernels in the memory-based diffusion term and find that the model exhibits complex dynamical behaviour produced by nonlocality and distributed memory. For either temporal kernel, mode-n Turing (or Hopf) bifurcation can emerge and double Turing bifurcation can be generated by mode-n and mode-m ($ n\neq m $) Turing bifurcations. Additionally, Hopf bifurcation is possible to occur for small random diffusion or large repulsive memory-based diffusion in considerations of weak or strong kernels, respectively. Note that the critical Turing bifurcation curve can be mode-n ($ n\geq2 $), which differs from that in the model with nonlocal spatial average, while Turing, Turing-Hopf and double Turing bifurcations do not appear in the single-species model involving only distributed memory delay. An application to our theoretical findings is presented and Turing-Hopf bifurcation and stability switches are found in numerical exploration by considering weak and strong kernels, respectively.
-
Keywords:
- Nonlocality /
- distributed memory /
- Turing bifurcation /
- Hopf bifurcation
-

-
References
[1] N. Britton, Aggregation and the competitive exclusion principle, J. Theor. Biol., 1989, 136(1), 57-66. doi: 10.1016/S0022-5193(89)80189-4 [2] S. Chen and J. Shi, Global attractivity of equilibrium in gierer-meinhardt system with activator production saturation and gene expression time delays, Nonlinear Anal. -Real World Appl., 2013, 14(4), 1871-1886. [3] W. F. Fagan, M. A. Lewis, M. Auger-Méthé and T. Avgar, Spatial memory and animal movement, Ecology Letters, 2013, 16(10), 1316-1329. [4] H. Hochstadt, Integral Equations, Wiley Interscience, New York, 1973. [5] Q. Ji, R. Wu and T. Zhang, Dynamics of a single population model with memory and nonlinear boundary condition, Appl. Anal., 2024. DOI: 10.1080/00036811.2024.2426229. [6] J. Lin and Y. Song, Spatially inhomogeneous periodic patterns induced by distributed memory in the memory-based single population model, Appl. Math. Lett., 2023, 137, 108490. doi: 10.1016/j.aml.2022.108490 [7] W. Ni, J. Shi and M. Wang, Global stability and pattern formation in a nonlocal diffusive Lotka-Volterra competition model, J. Differ. Equ., 2018, 264(11), 6891-6932. doi: 10.1016/j.jde.2018.02.002 [8] F. Riez and B. Sz-Nagy, Functional Analysis, Ungar, New York, 1955. [9] U. E. Schläegel and M. A. Lewis, Detecting effects of spatial memory and dynamic information on animal movement decisions, Methods Ecol. Evol., 2014, 5(11), 1236-1246. doi: 10.1111/2041-210X.12284 [10] H. Shen and Y. Song, Spatiotemporal patterns in a diffusive resource-consumer model with distributed memory and maturation delay, Math. Comput. Simul., 2024, 221, 622-644. doi: 10.1016/j.matcom.2024.03.026 [11] H. Shen, Y. Song and H. Wang, Bifurcations in a diffusive resource-consumer model with distributed memory, J. Differ. Equ., 2023, 347, 170-211. doi: 10.1016/j.jde.2022.11.044 [12] J. Shi and Q. Shi, Spatial movement with temporally distributed memory and dirichlet boundary condition, J. Differ. Equ., 2024, 389, 305-337. doi: 10.1016/j.jde.2024.01.022 [13] J. Shi, C. Wang and H. Wang, Diffusive spatial movement with memory and maturation delays, Nonlinearity, 2019, 32(9), 3188-3208. doi: 10.1088/1361-6544/ab1f2f [14] J. Shi, C. Wang, H. Wang and X. Yan, Diffusive spatial movement with memory, J. Dynam. Differential Equations, 2020, 32(2), 979-1002. doi: 10.1007/s10884-019-09757-y [15] Q. Shi, J. Shi and H. Wang, Spatial movement with distributed memory, J. Math. Biol., 2021, 82(4), 33. [16] Y. Song, S. Wu and H. Wang, Memory-based movement with spatiotemporal distributed delays in diffusion and reaction, Appl. Math. Comput., 2021, 404, 126254. [17] D. Wang and C. Wang, Dynamics of a diffusive two-species interaction model with memory effect, Discrete Contin. Dyn. Syst. -Ser. B, 2024. DOI: 10.3934/dcdsb.2024187. [18] S. Wu and Y. Song, Spatial movement with distributed memory and maturation delay, Qual. Theor. Dyn. Syst., 2024, 23(3), 117. -
-
-
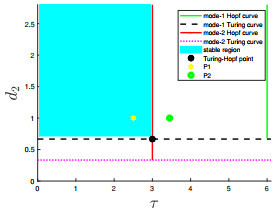
Figure 1.
The stable region of
$ u_\star=1 $ -
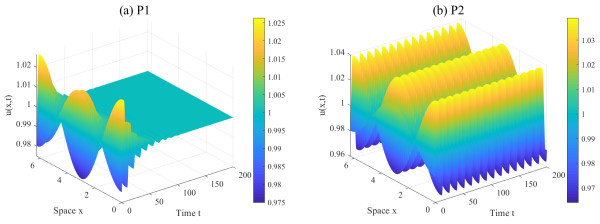
Figure 2.
The solutions for P1
$ (2.5,1) $ $ (3.45,1) $ $ 1-0.02\cos x $ -
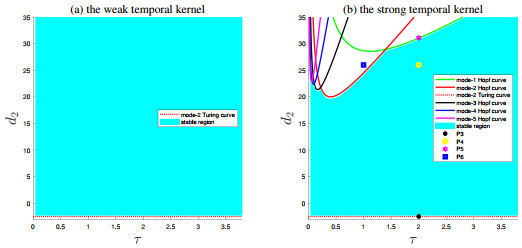
Figure 3.
The stable region of
$ u_\star=1 $ -
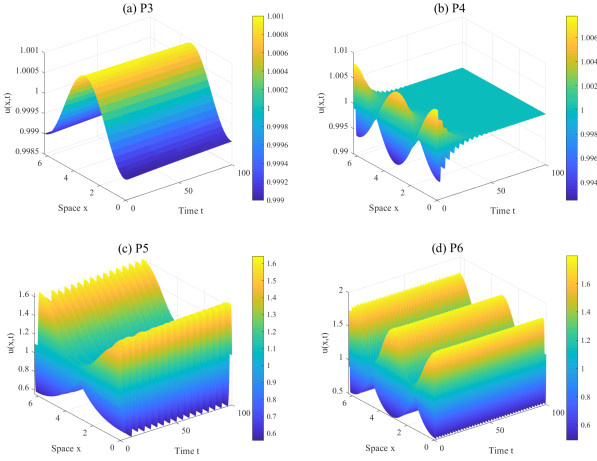
Figure 4.
The solutions for P3
$ (2,-2.5) $ $ (2,26) $ $ (2,31.1) $ $ (1,26) $ $ 1-0.001\cos x $ $ 1-0.001\cos x $ $ 1-0.1\cos 0.5x $ $ 1-0.1\cos x $




 DownLoad:
DownLoad: