| Citation: |
Xueying Shi, Xiaoping Chen, Chengdai Huang. DELAY-INDUCED HOPF BIFURCATION OF A FRACTIONAL-ORDER NEURAL NETWORK WITH BOTH NEUTRAL AND INERTIAL TERMS[J]. Journal of Applied Analysis & Computation, 2026, 16(1): 362-379. doi: 10.11948/20250068
|
DELAY-INDUCED HOPF BIFURCATION OF A FRACTIONAL-ORDER NEURAL NETWORK WITH BOTH NEUTRAL AND INERTIAL TERMS
-
Abstract
This paper focuses on the stability and bifurcation in a fractional-order neutral-type inertial neural network with time delay. We mainly analyze the new system with time delay by using Cramer's rule to derive precise bifurcation conditions. The accuracy of the theoretical findings is ultimately confirmed through two numerical experiments. Moreover, the remarkable advantages of the fractional-order model are found in delaying the occurrence of inherent bifurcations and enhancing the stability performance.
-
Keywords:
- Fractional-order /
- neural networks /
- stability /
- Hopf bifurcation /
- neutral and inertial terms
-
-
References
[1] K. L. Babcock and R. M. Westervelt, Stability and dynamics of simple electronic neural networks with added inertia, Physica D, 1986, 23, 464–469. doi: 10.1016/0167-2789(86)90152-1 [2] L. C. d. Barros, M. M. Lopes, F. S. Pedro, E. Esmi, J. P. C. d. Santos and D. E. Sánchez, The memory effect on fractional calculus: An application in the spread of COVID-19, Comput. Appl. Math., 2021, 40, 72. doi: 10.1007/s40314-021-01456-z [3] W. Deng, C. Li and J. Lü, Stability analysis of linear fractional differential system with multiple time delays, Nonlinear Dyn., 2007, 48, 409–416. doi: 10.1007/s11071-006-9094-0 [4] L. Duan, J. Jian and B. Wang, Global exponential dissipativity of neutral-type BAM inertial neural networks with mixed time-varying delays, Neurocomputing, 2020, 378, 399–412. doi: 10.1016/j.neucom.2019.10.082 [5] O. Faydasicok and S. Arik, The combined Lyapunov functionals method for stability analysis of neutral Cohen-Grossberg neural networks with multiple delays, Neural Netw., 2024, 180, 106641. doi: 10.1016/j.neunet.2024.106641 [6] J. Gao, C. Huang and H. Liu, Hopf bifurcations in a fractional-order neural network introducing delays into neutral terms, Eur. Phys. J. Plus, 2024, 139, 717. doi: 10.1140/epjp/s13360-024-05488-2 [7] L. Guo, H. Yue, Y. Wu and G. Xu, Complex spiking neural network with synaptic time delay evaluated by anti-damage capabilities under random attacks, Neurocomputing, 2024, 597, 127928. doi: 10.1016/j.neucom.2024.127928 [8] H. Hou, C. Luo and Z. Mo, On fractional ring neural networks with multiple time delays: Stability and Hopf bifurcation analysis, Chinese J. Phys., 2024, 90, 303–318. doi: 10.1016/j.cjph.2024.05.030 [9] C. Huang, J. Gao, S. Mo and J. Cao, Hopf bifurcation in a fractional-order neural network with self-connection delay, Nonlinear Dyn., 2023, 111, 14335–14350. doi: 10.1007/s11071-023-08553-0 [10] C. Huang, L. Fu, H. Wang, J. Cao and H. Liu, Extractions of bifurcation in fractional-order recurrent neural networks under neurons arbitrariness, Physica D, 2024, 468, 134279. doi: 10.1016/j.physd.2024.134279 [11] C. Huang, H. Liu, H. Wang, M. Xiao and J. Cao, Dynamical bifurcations of a fractional-order BAM neural network: Nonidentical neutral delays, IEEE T. Netw. Sci. Eng., 2024, 11, 1668–1679. doi: 10.1109/TNSE.2023.3329020 [12] C. Huang, S. Mo and Z. Wu, Novel results on bifurcations for a fractional-order neural network with neutral delays, Fractals, 2022, 30, 2250118. doi: 10.1142/S0218348X22501183 [13] C. Huang, H. Wang, J. Cao and H. Liu, Delay-dependent bifurcation conditions in a fractional-order inertial BAM neural network, Chaos Soliton. Fract., 2024, 185, 115106. doi: 10.1016/j.chaos.2024.115106 [14] Z. Jin, J. Cai, Y. Di, Y. Lei, F. Yu, Y. Liu and Y. Xu, Adaptive structure generation and neuronal differentiation for memory encoding in SNNs, Neurocomputing, 2024, 610, 128470. doi: 10.1016/j.neucom.2024.128470 [15] M. Kang, G. F. Templeton, D. H. Kwak and S. Um, Development of an AI framework using neural process continuous reinforcement learning to optimize highly volatile financial portfolios, Knowl-Based Syst., 2024, 300, 112017. doi: 10.1016/j.knosys.2024.112017 [16] S. Li, X. Song and C. Huang, Further study on the crossing curves in two-delay differential equations with delay-dependent coefficients, Appl. Math. Lett., 2024, 158, 109264. doi: 10.1016/j.aml.2024.109264 [17] I. Podlubny, Fractional Differential Equations, Academic Press, New York, 1999. [18] M. L. Shahab and H. Susanto, Neural networks for bifurcation and linear stability analysis of steady states in partial differential equations, Appl. Math. Comput., 2024, 483, 128985. [19] Y. Shen, J. Zhao and L. Yu, Reachable set estimation of delayed second-order memristive neural networks, Appl. Math. Comput., 2025, 484, 128994. [20] Y. Shou, X. Cao, H. Liu and D. Meng, Masked contrastive graph representation learning for age estimation, Pattern Recogn., 2025, 158, 110974. doi: 10.1016/j.patcog.2024.110974 [21] R. Suvetha, J. J. Nieto and P. Prakash, Non-fragile output-feedback control for delayed memristive bidirectional associative memory neural networks against actuator failure, Appl. Math. Comput., 2025, 485, 129021. [22] H. Wang, Y. Gu, X. Zhang and Y. Yu, Stability and synchronization of fractional-order reaction-diffusion inertial time-delayed neural networks with parameters perturbation, Neural Netw., 2024, 179, 106564. doi: 10.1016/j.neunet.2024.106564 [23] H. Wang, C. Huang, S. Li, J. Cao and H. Liu, Bifurcation detections of a fractional-order neural network involving three delays, J. Appl. Math. Comput., 2024, 70, 579–599. doi: 10.1007/s12190-023-01972-7 [24] H. Wang, X. Shangguan, D. Xiong, Y. An and L. Jin, A matrix-separation-based integral inequality for aperiodic sampled-data synchronization of delayed neural networks considering communication delay, Appl. Math. Comput., 2025, 486, 129032. [25] Y. Wei, Y. Chen, S. Cheng and Y. Wang, A note on short memory principle of fractional calculus, Fract. Calc. Appl. Anal., 2017, 20, 1382–1404. doi: 10.1515/fca-2017-0073 [26] D. W. Wheeler and W. C. Schieve, Stability and chaos in an inertial two-neuron system, Physica D, 1997, 105, 267–284. doi: 10.1016/S0167-2789(97)00008-0 [27] K. Wu and J. Jian, Non-reduced order strategies for global dissipativity of memristive neutral-type inertial neural networks with mixed time-varying delays, Neurocomputing, 2021, 436, 174–183. doi: 10.1016/j.neucom.2020.12.120 [28] P. Yadav, Cluster based-image descriptors and fractional hybrid optimization for medical image retrieval, Cluster Comput., 2019, 22, 1345–1359. doi: 10.1007/s10586-017-1625-6 [29] S. Yuan, Y. Wang, X. Zhang and X. Wang, H∞ anti-synchronization of switching inertial neural networks with leakage delays and mixed time-varying delays, Math. Comput. Simulat., 2024, 225, 619–647. doi: 10.1016/j.matcom.2024.06.004 -
-
Figures(18)
Export File
Citation
Xueying Shi, Xiaoping Chen, Chengdai Huang. DELAY-INDUCED HOPF BIFURCATION OF A FRACTIONAL-ORDER NEURAL NETWORK WITH BOTH NEUTRAL AND INERTIAL TERMS[J]. Journal of Applied Analysis & Computation, 2026, 16(1): 362-379. doi: 10.11948/20250068
Format
Content
DownLoad:
-
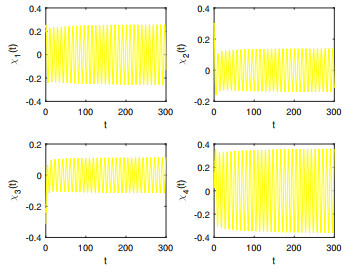
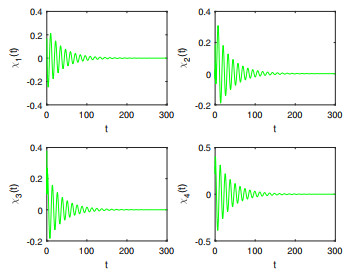
Figure 1.
The waveform diagrams of system (5.1) with
$ \varsigma=0.85<\varsigma_0=0.9733 $ -
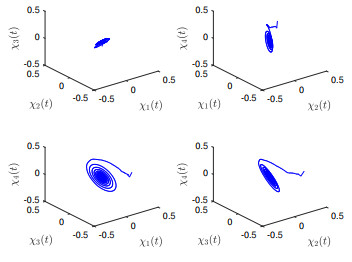
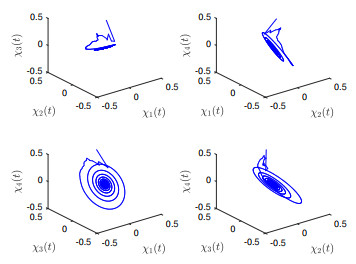
Figure 2.
The phase diagrams of system (5.1) with
$ \varsigma=0.85<\varsigma_0=0.9733 $ -
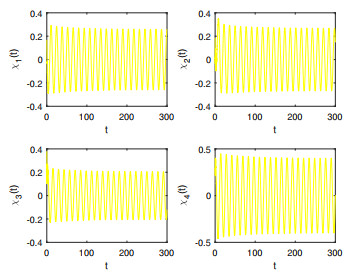
Figure 3.
The waveform diagrams of system (5.1) with
$ \varsigma=1.1>\varsigma_0=0.9733 $ -
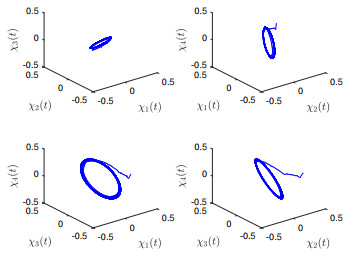
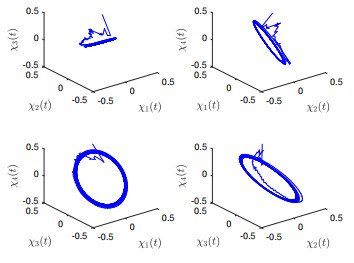
Figure 4.
The phase diagrams of system (5.1) with
$ \varsigma=1.1>\varsigma_0=0.9733 $ -
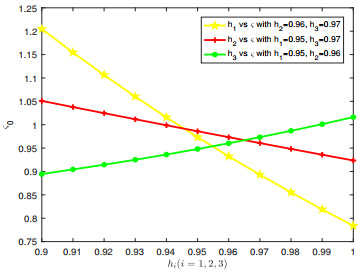
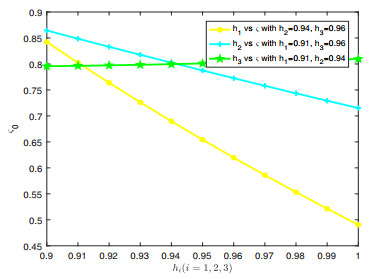
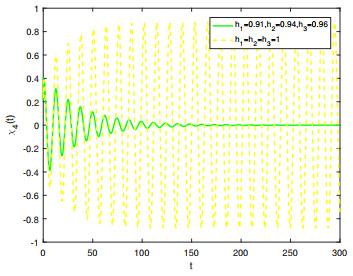
Figure 5.
Influence of
$ h_i $ $ \varsigma_0 $ -
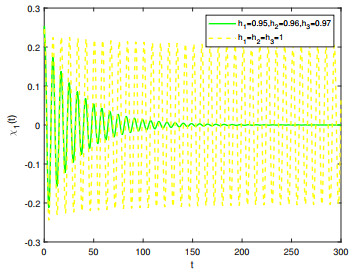
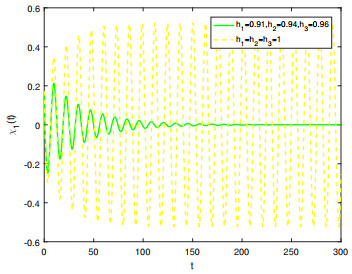
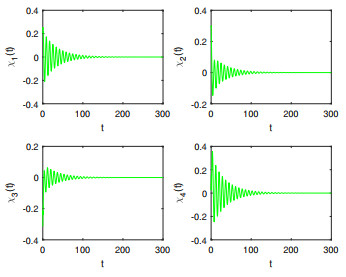
Figure 6.
Comparison on the stability of system (5.1) in integer-order and fractional-order.
-
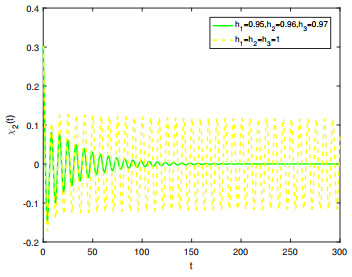
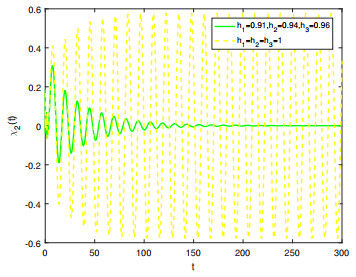
Figure 7.
Comparison on the stability of system (5.1) in integer-order and fractional-order.
-
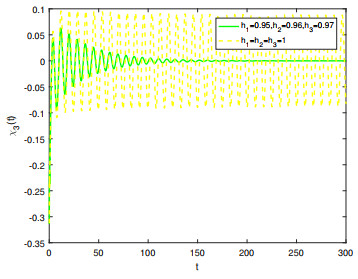
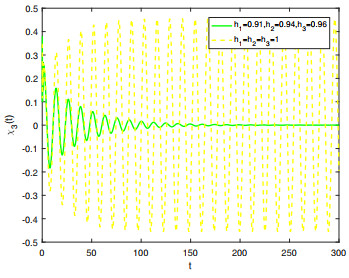
Figure 8.
Comparison on the stability of system (5.1) in integer-order and fractional-order.
-
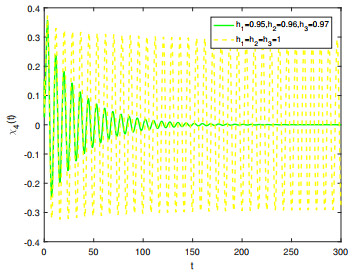
Figure 9.
Comparison on the stability of system (5.1) in integer-order and fractional-order.
-
Figure 10.
The waveform diagrams of system (5.2) with
$ \varsigma=0.65<\varsigma_0=0.8025 $ -
Figure 11.
The phase diagrams of system (5.2) with
$ \varsigma=0.65<\varsigma_0=0.8025 $ -
Figure 12.
The waveform diagrams of system (5.2) with
$ \varsigma=0.9<\varsigma_0=0.8025 $ -
Figure 13.
The phase diagrams of system (5.2) with
$ \varsigma=0.9>\varsigma_0=0.8025 $ -
Figure 14.
Influence of
$ h_i $ $ \varsigma_0 $ -
Figure 15.
Comparison on the stability of system (5.2) in integer-order and fractional-order.
-
Figure 16.
Comparison on the stability of system (5.2) in integer-order and fractional-order.
-
Figure 17.
Comparison on the stability of system (5.2) in integer-order and fractional-order.
-
Figure 18.
Comparison on the stability of system (5.2) in integer-order and fractional-order.