| Citation: |
Huan Dai, Mengfeng Sun. THE ASYMPTOTIC BOUNDS OF SOLUTIONS OF A GENERALIZED PANTOGRAPH EQUATION[J]. Journal of Applied Analysis & Computation, 2026, 16(1): 380-395. doi: 10.11948/20250064
|
THE ASYMPTOTIC BOUNDS OF SOLUTIONS OF A GENERALIZED PANTOGRAPH EQUATION
-
Abstract
This paper studies the asymptotic behavior of solutions of the generalized pantograph equation $ y'(t)=Ay(qt)+By(t)+Cy'(qt) $, where $ A, B, C $ are $ n×n $ complex matrices. By considering two cases of the coefficient matrix $ B $: Diagonalizable and non-diagonalizable, the asymptotic boundaries of solutions are discussed, respectively. When $ B $ is diagonalizable, the asymptotic boundary of solutions is dominated by the largest positive real part of the eigenvalues: If the smallest positive real part of eigenvalues exceeds the product of the delay parameter and the largest positive real part, then the components of solutions grow exponentially according to the corresponding eigenvalues, otherwise, all solutions are constrained by the largest positive real part of eigenvalues. When $ B $ cannot be diagonalized, the asymptotic boundary of solutions depends on the distribution of eigenvalues: If $ B $ has a unique multiple eigenvalue, then the real part of this eigenvalue determines the growth rate of solutions, otherwise, the components of solutions grow exponentially according to the corresponding eigenvalues in the Jordan blocks. Hence, every solution has an exponential asymptotic boundary, which depends on the eigenvalues of the coefficient matrix $ B $.
-
-
References
[1] I. Ahmad, R. Amin, T. Abdeljawad and K. Shah, A numerical method for fractional pantograph delay integro-differential equations on haar wavelet, Int. J. Appl. Comput. Math., 2021, 7, 1–13. doi: 10.1007/s40819-020-00933-z [2] H. Alrabaiah, I. Ahmad, K. Shah and G. Rahman, Qualitative analysis of nonlinear coupled pantograph differential equations of fractional order with integral boundary conditions, Bound. Value Probl., 2020, 2020, 1–13. doi: 10.1186/s13661-019-01311-5 [3] R. Alrebdi and H. Al-Jeaid, Two different analytical approaches for solving the pantograph delay equation with variable coefficient of exponential order, Axioms, 2024, 13(4), 229. doi: 10.3390/axioms13040229 [4] N. Barrouk and S. Mesbahi, Existence of global solutions of a reaction-diffusion system with a cross-diffusion matrix and fractional derivatives, Palest. J. Math., 2024, 13(3), 340–353. [5] M. Bohner, J. R. Graef and I. Jadlovská, Asymptotic properties of Kneser solutions to third-order delay differential equations, J. Appl. Anal. Comput., 2022, 12(5), 2024–2032. [6] M. Buhmann and A. Iserles, Stability of the discretized pantograph differential equation, Math. Comput., 1993, 60(202), 575–589. doi: 10.1090/S0025-5718-1993-1176707-2 [7] L. Fox, D. Mayers, J. Ockendon and A. Tayler, On a functional differential equation, IMA J. Appl. Math., 1971, 8(3), 271–307. doi: 10.1093/imamat/8.3.271 [8] J. Graef, I. Jadlovská and E. Tunç, Sharp asymptotic results for third-order linear delay differential equations, J. Appl. Anal. Comput., 2021, 11(5), 2459–2472. [9] R. Hilfer, Applications of Fractional Calculus in Physics, World Scientific, Singapore, 2000. [10] P. Höfer and A. Lion, Modelling of frequency-and amplitude-dependent material properties of filler-reinforced rubber, J. Mech. Phys. Solids, 2009, 57(3), 500–520. doi: 10.1016/j.jmps.2008.11.004 [11] M. Houas, K. Kaushik, A. Kumar, A. Khan and T. Abdeljawad, Existence and stability results of pantograph equation with three sequential fractional derivatives, AIMS Math., 2023, 8(3), 5216–5232. [12] A. Iserles, On the generalized pantograph functional-differential equation, Eur. J. Appl. Math., 1993, 4(1), 1–38. doi: 10.1017/S0956792500000966 [13] A. Iserles and Y. Liu, On pantograph integro-differential equations, J. Integral Equ. Appl., 1994, 213–237. [14] T. Jüngling, X. Porte, N. Oliver, M. Soriano and I. Fischer, A unifying analysis of chaos synchronization and consistency in delay-coupled semiconductor lasers, IEEE J. Sel. Top. Quant., 2019, 25(6), 1–9. [15] T. Kato and J. B. Mcleod, The functional-differential equation y′(x) = ay(λx) + by(x), B. Am. Math. Soc., 1971, 77(4), 21–22. [16] E. Lim, Asymptotic behavior of solutions of the functional differential equation x′(t) = Ax(λt) + Bx(t), λ > 0, J. Math. Anal. Appl., 1976, 55(3), 794–806. doi: 10.1016/0022-247X(76)90082-2 [17] W. Lu, T. Chen and G. Chen, Synchronization analysis of linearly coupled systems described by differential equations with a coupling delay, Physica D, 2006, 221(2), 118–134. doi: 10.1016/j.physd.2006.07.020 [18] T. Nabil, Solvability of nonlinear coupled system of urysohn-volterra quadratic integral equations in generalized banach algebras, J. Fract. Calc. Nonlin. Syst., 2024, 5(2), 16–32. [19] J. Ockendon and A. Tayler, The dynamics of a current collection system for an electric locomotive, Proc. R. Soc. Lond. A, 1971, 322(1551), 447–468. doi: 10.1098/rspa.1971.0078 [20] F. Rihan, Continuous Runge-Kutta schemes for pantograph type delay differential equations, J. Partial Differ. Equ. Appl. Math. , 2024, 11, 100797. [21] K. Shah, I. Ahmad, J. Nieto, G. Rahman and T. Abdeljawad, Qualitative investigation of nonlinear fractional coupled pantograph impulsive differential equations, Qual. Theor. Dyn. Syst., 2022, 21(4), 131. doi: 10.1007/s12346-022-00665-z [22] N. Sriwastav, A. Barnwal, A. Wazwaz and M. Singh, A novel numerical approach and stability analysis for a class of pantograph delay differential equation, J. Comput. Sci-Neth., 2023, 67, 101976. doi: 10.1016/j.jocs.2023.101976 [23] C. Zhang, Analytical study of the pantograph equation using Jacobi theta functions, J. Approx. Theory, 2023, 296, 105974. doi: 10.1016/j.jat.2023.105974 -
-
Figures(4)
Export File
Citation
Huan Dai, Mengfeng Sun. THE ASYMPTOTIC BOUNDS OF SOLUTIONS OF A GENERALIZED PANTOGRAPH EQUATION[J]. Journal of Applied Analysis & Computation, 2026, 16(1): 380-395. doi: 10.11948/20250064
Format
Content
DownLoad:
-
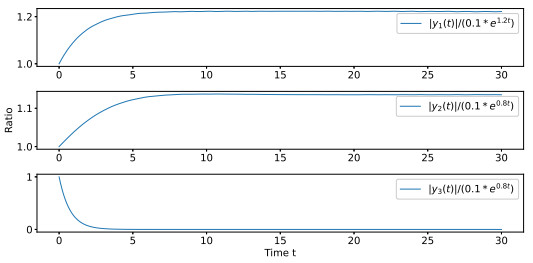
Figure 1.
The ratio of
$ |y_1(t)|/(0.1{\rm e}^{1.2t}) $ $ |y_2(t)|/(0.1{\rm e}^{0.8t}) $ $ |y_3(t)|/(0.1{\rm e}^{0.8t}) $ -
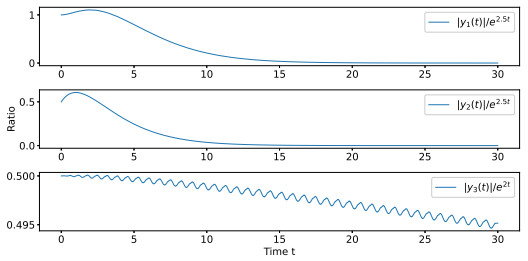
Figure 2.
The ratio of
$ |y_1(t)|/{\rm e}^{2.5t} $ $ |y_2(t)|/{\rm e}^{2.5t} $ $ |y_3(t)|/{\rm e}^{2t} $ -
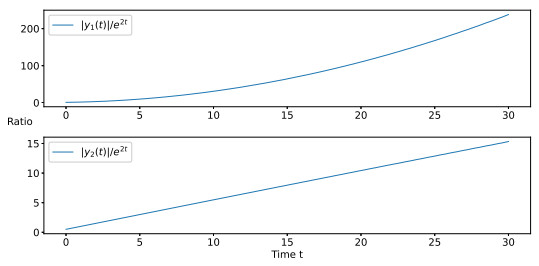
Figure 3.
The ratio of
$ |y_1(t)|/{\rm e}^{2t} $ $ |y_2(t)|/{\rm e}^{2t} $ -
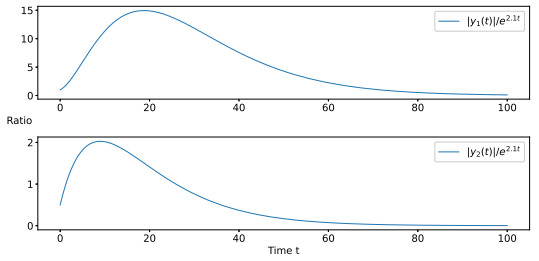
Figure 4.
The ratio of
$ |y_1(t)|/{\rm e}^{2.1t} $ $ |y_2(t)|/{\rm e}^{2.1t} $