| Citation: | Minghui Liu, Jiqiang Jiang. EXISTENCE OF POSITIVE SOLUTIONS FOR COUPLED FRACTIONAL DIFFERENTIAL SYSTEM WITH IMPROPER INTEGRAL BOUNDARY CONDITIONS ON THE HALF-LINE[J]. Journal of Applied Analysis & Computation, 2026, 16(1): 396-425. doi: 10.11948/20250110 |
EXISTENCE OF POSITIVE SOLUTIONS FOR COUPLED FRACTIONAL DIFFERENTIAL SYSTEM WITH IMPROPER INTEGRAL BOUNDARY CONDITIONS ON THE HALF-LINE
-
Abstract
This article is devoted to proving the existence of positive solutions for a class of coupled fractional boundary value problems involving an improper integral and the infinite-point on the half-line. By making use of the monotone iterative technique along with Banach's contraction mapping principle, some explicit monotone iterative sequences for approximating the extreme positive solutions and the unique positive solution for the problem are constructed, an error estimate formula of the positive solution is also given. In the end, a numerical simulation is given to illustrate the main results.
-

-
References
[1] S. Abbas, S. Tyagi, P. Kumar, V. S. Ertürk and S. Momani, Stability and bifurcation analysis of a fractional-order model of cell-to-cell spread of hiv-1 with a discrete time delay, Math. Methods Appl. Sci., 2022, 45(11), 7081–7095. doi: 10.1002/mma.8226 [2] B. Ahmad and J. J. Nieto, Existence results for a coupled system of nonlinear fractional differential equations with three-point boundary conditions, Comput. Math. Appl., 2009, 58(9), 1838–1843. doi: 10.1016/j.camwa.2009.07.091 [3] S. Aljoudi, B. Ahmad, J. J. Nieto and A. Alsaedi, A coupled system of Hadamard type sequential fractional differential equations with coupled strip conditions, Chaos Solitons Fractals, 2016, 91, 39–46. doi: 10.1016/j.chaos.2016.05.005 [4] D. A. Benson, S. W. Wheatcraft and M. M. Meerschaert, Application of a fractional advection-dispersion equation, Water Resour. Res., 2000, 36(6), 1403–1412. doi: 10.1029/2000WR900031 [5] T. S. Cerdik and F. Y. Deren, New results for higher-order Hadamard-type fractional differential equations on the half-line, Math. Methods Appl. Sci., 2022, 45(4), 2315–2330. doi: 10.1002/mma.7926 [6] X. Chen, W. Yang, X. Zhang and F. Liu, Unsteady boundary layer flow of viscoelastic mhd fluid with a double fractional maxwell model, Appl. Math. Lett., 2019, 95, 143–149. doi: 10.1016/j.aml.2019.03.036 [7] W. Cheng, J. Xu, Y. Cui and Q. Ge, Positive solutions for a class of fractional difference systems with coupled boundary conditions, Adv. Difference Equ., 2019, 2019, 249. DOI: 10.1186/s13662-019-2184-3. [8] A. Deep and M. Kazemi, Solvability for 2D non-linear fractional integral equations by petryshyn's fixed point theorem, J. Comput. Appl. Math., 2024, 444, 115797. doi: 10.1016/j.cam.2024.115797 [9] J. Eggleston and S. Rojstaczer, Identification of large-scale hydraulic conductivity trends and the influence of trends on contaminant transport, Water Resour. Res., 1998, 34(9), 2155–2168. doi: 10.1029/98WR01475 [10] T. Jessada, S. K. Ntouyas, S. Asawasamrit and C. Promsakon, Positive solutions for Hadamard differential systems with fractional integral conditions on an unbounded domain, Open Math., 2017, 15(1), 645–666. doi: 10.1515/math-2017-0057 [11] J. Jiang and X. Sun, Existence of positive solutions for a class of p-Laplacian fractional differential equations with nonlocal boundary conditions, Bound. Value Probl., 2024, 2024, 97. DOI: 10.1186/s13661-024-01905-8. [12] M. Kazemi, R. Ezzati and A. Deep, On the solvability of non-linear fractional integral equations of product type, J. Pseudo-Differ. Oper. Appl., 2023, 14(3), 39. doi: 10.1007/s11868-023-00532-8 [13] M. Kazemi, R. Rahul and A. Yaghoobnia, Applications of measure of noncompactness for solvability of Hadamard fractional integral equations, Comput. Appl. Math., 2025, 44, 30. doi: 10.1007/s40314-024-03005-w [14] A. A. Kilbas, H. M. Srivastava and J. J. Trujillo, Theory and Applications of Fractional Differential Equations, Amsterdam, Elsevier, 2006. [15] S, Li, Z. Zhang and W. Jiang, Multiple positive solutions for four-point boundary value problem of fractional delay differential equations with p-Laplacian operator, Appl. Numer. Math., 2021, 165, 348–356. doi: 10.1016/j.apnum.2021.03.001 [16] Y. Li, S. Bai and D. O'Regan, Monotone iterative positive solutions for a fractional differential system with coupled Hadamard type fractional integral conditions, J. Appl. Anal. Comput., 2023, 13(3), 1556–1580. [17] R. Luca and A. Tudorache, Existence of solutions for a Hadamard fractional boundary value problem at resonance, Fractal Fract., 2025, 9(2), 119. doi: 10.3390/fractalfract9020119 [18] M. Moghaddamfar, M. Kazemi and R. Ezzati, Existence results for generalized 2D fractional partial integro-differential equations, J. Comput. Appl. Math., 2026, 471, 116705. doi: 10.1016/j.cam.2025.116705 [19] N. Nyamoradi and B. Ahmad, Hadamard fractional differential equations on an unbounded domain with integro-initial conditions, Qual. Theory Dyn. Syst., 2024, 23(4), 183. doi: 10.1007/s12346-024-01044-6 [20] K. Pei, G, Wang and Y. Sun, Successive iterations and positive extremal solutions for a Hadamard type fractional integro-differential equations on infinite domain, Appl. Math. Comput., 2017, 312, 158–168. [21] R. Poovarasan and V. Govindaraj, Existence of solutions for a coupled system of ψ-Caputo fractional differential equations with integral boundary conditions, Math. Methods Appl. Sci., 2025, 48(9), 9456–9468. doi: 10.1002/mma.10810 [22] J. Sabatier, O. P. Agrawal and J. T. Machado, Advances in Fractional Calculus, Volume 4, Springer, 2007. [23] X. Su and S. Zhang, Unbounded solutions to a boundary value problem of fractional order on the half-line, Comput. Math. Appl., 2011, 61(4), 1079–1087. doi: 10.1016/j.camwa.2010.12.058 [24] P. Thiramanus, S. K. Ntouyas and J. Tariboon, Positive solutions for Hadamard fractional differential equations on infinite domain, Adv. Difference Equ., 2016, 2016, 83. DOI: 10.1186/s13662-016-0813-7. [25] G. Wang, K. Pei, R. P. Agarwal, L. Zhang and B. Ahmad, Nonlocal Hadamard fractional boundary value problem with Hadamard integral and discrete boundary conditions on a half-line, J. Comput. Appl. Math., 2018, 343, 230–239. doi: 10.1016/j.cam.2018.04.062 [26] N. Wang and Z. Zhou, Multiple positive solutions of fractional differential equations with improper integral boundary conditions on the half-line, Bound. Value Probl., 2023, 2023, 88. DOI: 10.1186/s13661-023-01777-4. [27] Y. Wang and H. Wang, Triple positive solutions for fractional differential equation boundary value problems at resonance, Appl. Math. Lett., 2020, 106, 106376. doi: 10.1016/j.aml.2020.106376 [28] D. Yang and K. Zhu, Start-up flow of a viscoelastic fluid in a pipe with a fractional maxwell's model, Comput. Math. Appl., 2010, 60(8), 2231–2238. doi: 10.1016/j.camwa.2010.08.013 [29] H. Zhang, Y. Wang and J. Xu, Explicit monotone iterative sequences for positive solutions of a fractional differential system with coupled integral boundary conditions on a half-line, Adv. Difference Equ., 2020, 2020, 396. DOI: 10.1186/s13662-020-02860-1. [30] L. Zhang, X. Liu, Z. Yu and M. Jia, The existence of positive solutions for high order fractional differential equations with sign changing nonlinearity and parameters, AIMS Math., 2023, 8(11), 25990–26006. doi: 10.3934/math.20231324 [31] W. Zhang and J. Ni, New multiple positive solutions for Hadamard-type fractional differential equations with nonlocal conditions on an infinite interval, Appl. Math. Lett., 2021, 118, 107165. doi: 10.1016/j.aml.2021.107165 [32] X. Zhang, D. Kong, H. Tian, Y. Wu and B. Wiwatanapataphee, An upper-lower solution method for the eigenvalue problem of Hadamard-type singular fractional differential equation, Nonlinear Anal. Model. Control, 2022, 27(4), 789–802. [33] X. Zhang and Q. Zhong, Triple positive solutions for nonlocal fractional differential equations with singularities both on time and space variables, Appl. Math. Lett., 2018, 80, 12–19. doi: 10.1016/j.aml.2017.12.022 -
-
-
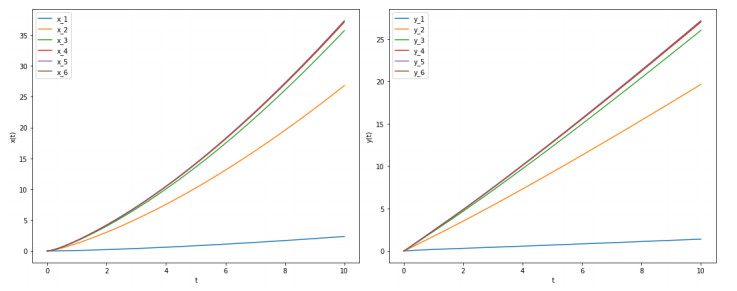
Figure 1.
The iterative process of
$ x_n $ $ y_n $ -
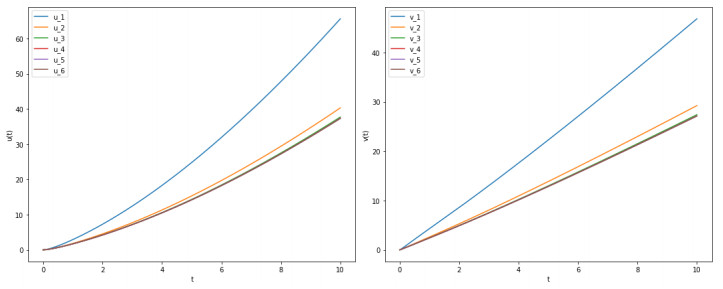
Figure 2.
The iterative process of
$ u_n $ $ v_n $




 DownLoad:
DownLoad: