| Citation: |
Seda Igret Araz. SEASONALITY OF RICKER MUTUALISM MODEL EMPLOYING RATE INDICATOR WITH ALMOST PERIODIC FUNCTION[J]. Journal of Applied Analysis & Computation, 2026, 16(1): 312-327. doi: 10.11948/20250096
|
SEASONALITY OF RICKER MUTUALISM MODEL EMPLOYING RATE INDICATOR WITH ALMOST PERIODIC FUNCTION
-
Abstract
In this paper, we implement a rate indicator function featuring an almost periodic component to capture seasonal trends within the Ricker model, which represents a mutualistic framework. For the updated model incorporating this function, we derived parameters that guarantee the uniqueness of the solution and confirmed that the initial conditions do not affect the solution. We anticipate that this study will provide valuable insights into the critical role of the rate indicator function and the influence of almost periodicity in analyzing seasonal trends.
-
Keywords:
- Almost periodicity /
- ecological model /
- seasonality /
- rate indicator
-
-
References
[1] S. Altizer, A. Dobson, P. Hosseini, P. Hudson, M. Pascual and R. Pejman, Seasonality and the dynamics of infectious diseases, Ecol. Lett., 2006, 9, 467-484. doi: 10.1111/j.1461-0248.2005.00879.x [2] S. Igret Araz and S. Boulaaras, Fractional modeling of gradual incorporation of infected prey into the predator-prey system with consideration of seasonality, Applied Mathematics in Science and Engineering, 2025, 33(1). [3] I. K. Argyros and D. Chen, The midpoint method for solving nonlinear operator equations in Banach space, Appl. Math. Lett., 1992, 5, 7-9. [4] I. Akbulut Arık and C. Tunc, On the periodic solutions of neutral integro-differential equations via fixed point method, Journal of Mathematical Analysis, 2022, 13(5), 35-48. doi: 10.54379/jma-2022-5-4 [5] A. Atangana and S. Igret Araz, Step forward in epidemiological modeling: Introducing the indicator function to capture waves%, Results in Physics, 2022, 38. [6] H. Bohr, Almost Periodic Funct, Chelsea Publishing Company, New York, 1947. [7] M. A. Cetin and S. Igret Araz, Prediction of Covid-19 spread with models in different patterns: A case study of Russia, Open Physics, 2024, 22. [8] S. Endre and M. David, An Introduction to Numerical Analysis, Cambridge University Press, New York, 2003. [9] M. W. Hirsch, System of differential equations which are competitive or cooperative: Limit sets, SIAM J. Math. Anal., 1982, 13(2). [10] J. Huang, S. Ruan, X. Wu and X. Zhou, Seasonal transmission dynamics of measles in China, Theory Biosci., 2018, 137, 185-195. doi: 10.1007/s12064-018-0271-8 [11] M. A. Ibrahim and A. Dénes, Stability and threshold dynamics in a seasonal mathematical model for measles outbreaks with double-dose vaccination, Mathematics, 2023, 11, 1791. doi: 10.3390/math11081791 [12] M. Kulakov, G. Neverova and E. Frisman, The Ricker competition model of two species: Dynamic modes and phase multistability, Mathematics, 2022, 10, 1076. doi: 10.3390/math10071076 [13] S. Kundu and S. Saha, Dynamics of a Ricker-type mutualistic system with time delay, Mathematical Biosciences, 2019, 314, 1-11. doi: 10.1016/j.mbs.2019.05.004 [14] H. G. Díaz-Marín, S. Shaday Guerrero-Flores, O. Osuna and G. Villavicencio-Pulido, A class of mutualistic systems having an almost periodic global attractor, Differential Equations and Dynamical Systems, 2023, 33, 123-140. [15] H. G. Díaz-Marín, F. López-Hernández and O. Osuna, Almost periodic solutions for seasonal cooperative systems, Annal. Polonici Mathematici, 2022, 128, 1-14. doi: 10.4064/ap210128-19-8 [16] R. M. May, Models for Two Interacting Populations, in Theoretical Ecology: Principles and Applications, University of Michigan, New York, 1976. [17] C. Rebelo, A. Margheri and N. Bacaër, Persistence in seasonally forced epidemiological models, J. Math. Biol. 2012, 64, 933-949. doi: 10.1007/s00285-011-0440-6 [18] W. E. Ricker, Stock and recruitment, Journal of the Fisheries Research Board of Canada, 1954, 11(5), 559-623. doi: 10.1139/f54-039 [19] H. L. Smith, Monotone Dynamical Systems: An Introduction to the Theory of Competitive and Cooperative Systems, American Mathematical Society, Rhode Island, USA, 1995. [20] B. G. Wang, L. Qiang and Z. C. Wang, An almost periodic ross-macdonald model with structured vector population in a patchy environment, J. Math. Biol., 2019, 80, 835-863. [21] R. Wu and L. Li, Note on the stability property of the boundary equilibrium of a may cooperative system with strong and weak cooperative partners, J. Math. Comp. Sci., 2020, 20, 58-63. -
-
Figures(10)
Export File
Citation
Seda Igret Araz. SEASONALITY OF RICKER MUTUALISM MODEL EMPLOYING RATE INDICATOR WITH ALMOST PERIODIC FUNCTION[J]. Journal of Applied Analysis & Computation, 2026, 16(1): 312-327. doi: 10.11948/20250096
Format
Content
DownLoad:
-
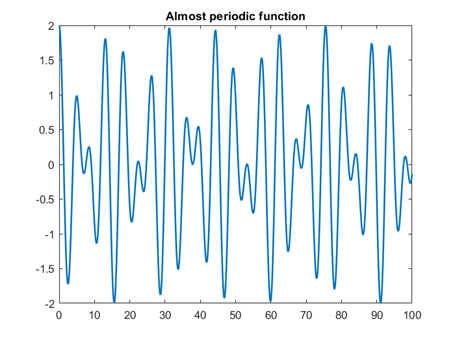
Figure 1.
Graphical representation of the almost periodic function presented in Example 1.1.
-
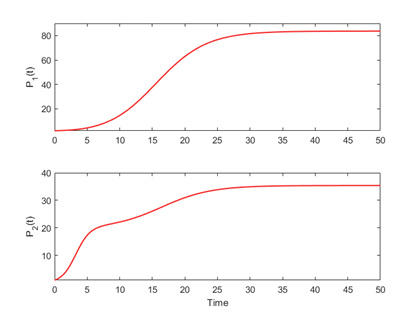
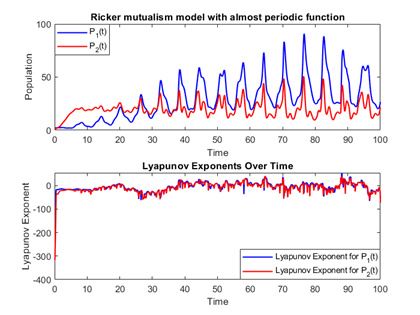
Figure 2.
Simulation showing the dynamics of the Ricker mutualism model in the absence of the almost periodic function.
-
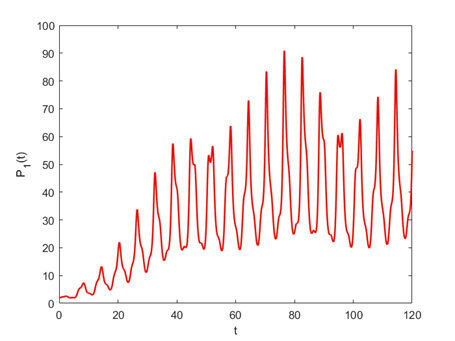
Figure 3.
Graphical representation of the dynamics of the function
$ P_{1}(t) $ -
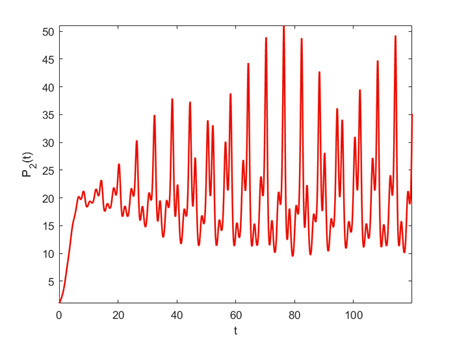
Figure 4.
Graphical representation of the dynamics of the function
$ P_{2}(t) $ -
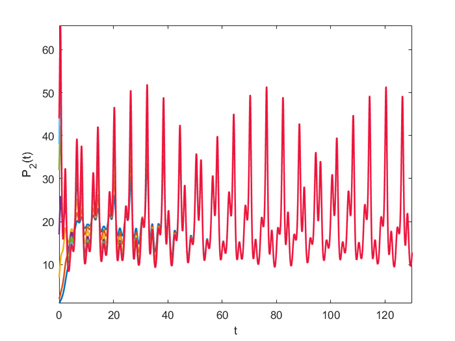
Figure 5.
Simulation of the function
$ P_{1}\left(t\right) $ -
Figure 6.
Simulation of the function
$ P_{2}\left(t\right) $ -
Figure 7.
Lyapunov exponents of Ricker's mutualism model with rate indicator function.
-
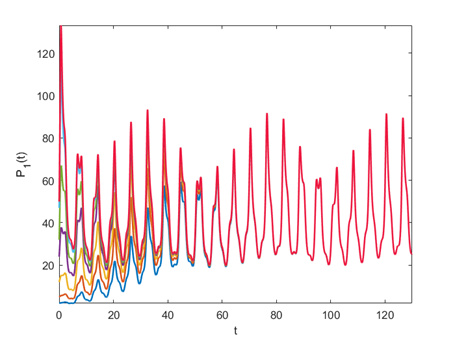
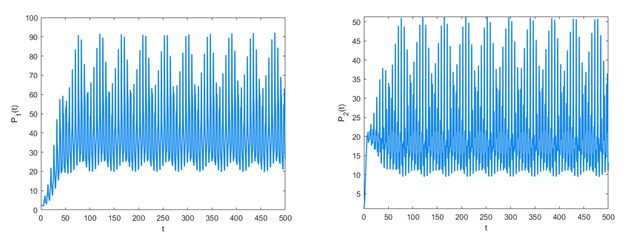
Figure 8.
Graphical representation of each variable of the Ricker mutualism model with the rate indicator function over an extended time interval.
-
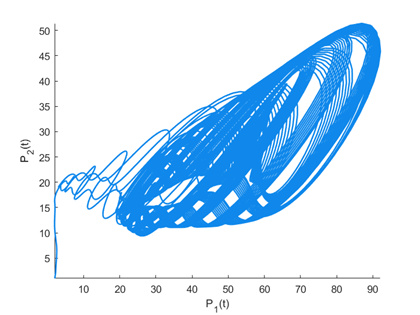
Figure 9.
Phase plot of
$ P_{2}\left( t\right) $ $ P_{1}\left( t\right) $ -
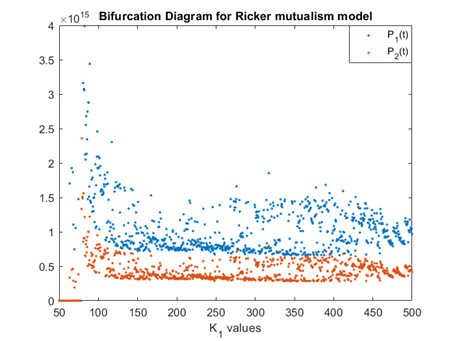
Figure 10.
Bifurcation diagram of the Ricker mutualism model with the rate indicator function for varying values of
$ K_{1} $