| Citation: | Tao Feng, Mingkang Ni. ASYMPTOTIC SOLUTION FOR A SYSTEM OF SINGULARLY PERTURBED DELAY DIFFERENTIAL EQUATIONS[J]. Journal of Applied Analysis & Computation, 2026, 16(1): 458-478. doi: 10.11948/20250097 |
ASYMPTOTIC SOLUTION FOR A SYSTEM OF SINGULARLY PERTURBED DELAY DIFFERENTIAL EQUATIONS
-
Abstract
This paper is mainly aimed to investigate the asymptotic solution for a system of singularly perturbed delay differential equations. In order to establish the step—like asymptotic solution, the basic framework of contrast structure theory is employed. Some sufficient criteria for the existence of asymptotic solution will be proposed. After that, by means of the boundary layer functions method and sewing method, the expansion for the asymptotic solution will be constructed and the existence of a uniformly valid continuous solution is proved. Finally, the effectiveness of the established results is validated via a concrete example.
-
Keywords:
- Asymptotic solution /
- singular perturbation /
- delay /
- boundary layer functions /
- contrast structure
-

-
References
[1] K. Aarthika, V. Shanthi and H. Ramos, A non–uniform difference scheme for solving singularly perturbed 1D–parabolic reaction–convection–diffusion systems with two small parameters and discontinuous source terms, J. Math. Chem., 2020, 58(3), 663–685. doi: 10.1007/s10910-019-01094-1 [2] V. F. Butuzov, Asymptotic behavior and stability of a stationary boundary–layer solution to a partially dissipative system of equations, Comput. Math. Math. Phys., 2019, 59(7), 1148–1171. doi: 10.1134/S0965542519070145 [3] V. F. Butuzov, Asymptotic expansion of the solution to a partially dissipative system of equations with a multizone boundary layer, Comput. Math. Math. Phys., 2019, 59(10), 1672–1692. doi: 10.1134/S0965542519100051 [4] F. Candelier and O. Vauquelin, Matched asymptotic solutions for turbulent plumes, J. Fluid. Mech., 2012, 699, 489–499. doi: 10.1017/jfm.2012.134 [5] P. P. Chakravarthy and K. Kumar, A novel method for singularly perturbed delay differential equations of reaction–diffusion type, Differ. Equ. Dyn. Syst., 2021, 29(3), 723–734. doi: 10.1007/s12591-017-0399-x [6] H. G. Debela and G. F. Duressa, Parametric uniform numerical method for singularly perturbed differential equations having both small and large delay, Acta Univ. Sapientiae Math., 2023, 15(1), 54–69. doi: 10.2478/ausm-2023-0004 [7] S. Elango, Second order singularly perturbed delay differential equations with non–local boundary condition, J. Comput. Appl. Math., 2023, 417, 114498. doi: 10.1016/j.cam.2022.114498 [8] F. Erdogan and G. M. Amiraliyev, Fitted finite difference method for singularly perturbed delay differential equations, Numer. Algorithms, 2012, 59(1), 131–145. doi: 10.1007/s11075-011-9480-7 [9] T. Feng and M. K. Ni, Internal layers for a quasi–linear singularly perturbed delay differential equation, J. Appl. Anal. Comput., 2020, 10(4), 1666–1682. [10] Z. Gajic, D. Petkovski and N. Harkara, The recursive algorithm for the optimal static output feedback control problem of linear singularity perturbed systems, IEEE T. Automat. Control, 1989, 34(4), 465–468. doi: 10.1109/9.28027 [11] V. Y. Glizer, Asymptotic analysis and solution of a finite–horizon H∞ control problem for singularly–perturbed linear systems with small state delay, J. Optim. Theory Appl., 2003, 117(2), 295–325. doi: 10.1023/A:1023631706975 [12] K. Gopalsamy, Stability and Oscillations in Delay Differential Equations of Population Dynamics, Springer, Dordrecht, 1992. [13] D. Joy and S. D. Kumar, Numerical method for solving weakly coupled systems of singularly perturbed delay differential equations, Comput. Appl. Math., 2024, 43(8), 419. doi: 10.1007/s40314-024-02932-y [14] D. Joy and S. D. Kumar, Liouville–Green transformation technique to solve singularly perturbed delay differential equations of reaction diffusion type, Math. Meth. Appl. Sci., 2025, 48(10), 10314–10331. doi: 10.1002/mma.10247 [15] D. Joy, S. D. Kumar and F. A. Rihan, Advancing numerical solutions for a system of singularly perturbed delay differential equations at linear rate, Bound. Value Probl., 2025, 2025, 15. doi: 10.1186/s13661-025-02000-2 [16] T. Kajiwara, T. Sasaki and Y. Takeuchi, Construction of Lyapunov functionals for delay differential equations in virology and epidemiology, Nonlinear Anal. Real World Appl., 2012, 13(4), 1802–1826. doi: 10.1016/j.nonrwa.2011.12.011 [17] M. Kamenskii and P. Nistri, An averaging method for singularly perturbed systems of semilinear differential inclusions with C0–semigroups, Set–Valued Anal., 2003, 11(4), 345–357. doi: 10.1023/A:1025604317289 [18] A. Kaushik, Singular perturbation analysis of bistable differential equation arising in the nerve pulse propagation, Nonlinear Anal. Real World Appl., 2008, 9(5), 2106–2127. doi: 10.1016/j.nonrwa.2007.06.014 [19] I. Kubiaczyk and S. H. Saker, Oscillation and stability in nonlinear delay differential equations of population dynamics, Math. Comput. Modelling, 2002, 35(3–4), 295–301. doi: 10.1016/S0895-7177(01)00166-2 [20] C. Kuehn, Multiple Time Scale Dynamics, Springer, Switzerland, 2015. [21] C. G. Lange and R. M. Miura, Singular perturbation analysis of boundary value problems for differential–difference equations, SIAM J. Appl. Math., 1982, 42(3), 502–531. doi: 10.1137/0142036 [22] A. Longtin and J. G. Milton, Complex oscillations in the human pupil light reflex with “mixed” and delayed feedback, Math. Biosci., 1988, 90(1–2), 183–199. doi: 10.1016/0025-5564(88)90064-8 [23] A. Longtin and J. G. Milton, Insight into the transfer function, gain, and oscillation onset for the pupil light reflex using nonlinear delay–differential equations, Biol. Cybernet., 1989, 61(1), 51–58. doi: 10.1007/BF00204759 [24] R. A. Mariya and S. D. Kumar, Fitted mesh cubic spline tension method for singularly perturbed delay differential equations with integral boundary condition, Comput. Methods Differ. Equ., 2025, 13(2), 618–633. [25] A. A. Melnikova and M. Chen, Existence and asymptotic representation of the autowave solution of a system of equations, Comput. Math. Math. Phys., 2018, 58(5), 680–690. doi: 10.1134/S0965542518050147 [26] J. D. Murray, Mathematical Biology: I. An Introduction, Springer, New York, 2002. [27] A. H. Nayfeh, Perturbation Methods, Wiley, New York, 2000. [28] M. K. Ni, On the internal layer for a singularly perturbed system of second–order delay differential equations, Differ. Equ., 2013, 49(8), 941–954. doi: 10.1134/S001226611308003X [29] M. K. Ni, N. N. Nefedov and N. T. Levashova, Asymptotics of the solution of a singularly perturbed second–order delay differential equation, Differ. Equ., 2020, 56(3), 290–303. doi: 10.1134/S0012266120030027 [30] Y. F. Pang, M. K. Ni and N. T. Levashova, Internal layer for a system of singularly perturbed equations with discontinuous right–hand side, Differ. Equ., 2018, 54(12), 1583–1594. doi: 10.1134/S0012266118120054 [31] L. Prandtl, Über flüssigkeitsbewegung bei sehr kleiner reibung (in German), Verhandlg. Ⅲ, Intern. Math. Kongr., Heidelberg, 1904, 484–491. [32] N. Sun, S. Y. Shi and W. L. Li, Singular renormalization group approach to SIS problems, Discrete Contin. Dyn. Syst. Ser. B, 2020, 25(9), 3577–3596. [33] S. K. Tesfaye, T. G. Dinka, M. M. Woldaregay and G. F. Duressa, Numerical analysis for a singularly perturbed parabolic differential equation with a time delay, Comput. Math. Math. Phys., 2024, 64(3), 537–554. doi: 10.1134/S096554252403014X [34] R. Vallée, P. Dubois, M. Coté and C. Delisle, Second–order differential–delay equation to describe a hybrid bistable device, Phy. Rev. A, 1987, 36(3), 1327–1332. doi: 10.1103/PhysRevA.36.1327 [35] A. B. Vasil'eva, On contrast structures of step type for a system of singularly perturbed equations, Comput. Math. Math. Phys., 1994, 34(10), 1215–1223. [36] A. B. Vasil'eva and V. F. Butuzov, Asymptotic Expansions of the Solutions of Singularly Perturbed Equations, Nauka, Moscow, 1973. [37] A. B. Vasil'eva, V. F. Butuzov and L. V. Kalachev, The Boundary Function Method for Singular Perturbation Problems, SIAM, Philadelphia, 1995. [38] C. Wang and X. Zhang, Canards, heteroclinic and homoclinic orbits for a slow–fast predator–prey model of generalized Holling type Ⅲ, J. Differential Equations, 2019, 267(6), 3397–3441. doi: 10.1016/j.jde.2019.04.008 [39] K. Wang, Z. J. Du and J. Liu, Traveling pulses of coupled FitzHugh–Nagumo equations with doubly–diffusive effect, J. Differential Equations, 2023, 374, 316–338. doi: 10.1016/j.jde.2023.07.027 [40] L. M. Wu, M. K. Ni and H. B. Lu, Internal layer solution of singularly perturbed optimal control problem with integral boundary condition, Qual. Theory Dyn. Syst., 2018, 17(1), 49–66. doi: 10.1007/s12346-017-0261-0 [41] L. Xu, Z. G. Xu, W. L. Li and S. Y. Shi, Renormalization group approach to a class of singularly perturbed delay differential equations, Commun. Nonlinear Sci. Numer. Simul., 2021, 103, 106028. doi: 10.1016/j.cnsns.2021.106028 [42] H. Yüce and C. Y. Wang, A boundary perturbation method for circularly periodic plates with a core, J. Sound Vibration, 2009, 328(3), 345–368. doi: 10.1016/j.jsv.2009.08.006 -
-
-
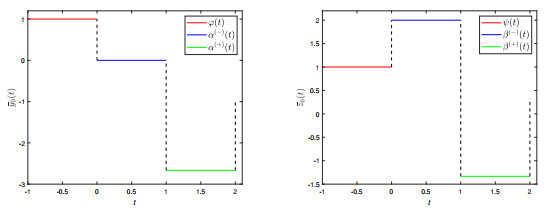
Figure 1.
Graph of the degenerate solutions
$ \bar y_0(t) $ $ \bar z_0(t) $ $ t $ -
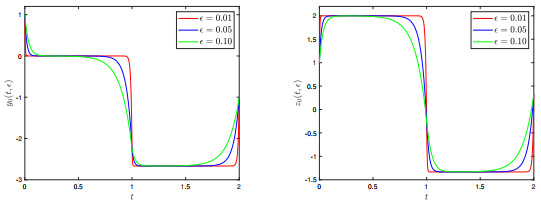
Figure 2.
Graph of the first–order continuous asymptotic solution
$ \left(y_0(t,\epsilon),z_0(t,\epsilon)\right)^\top $ $ \epsilon $




 DownLoad:
DownLoad: