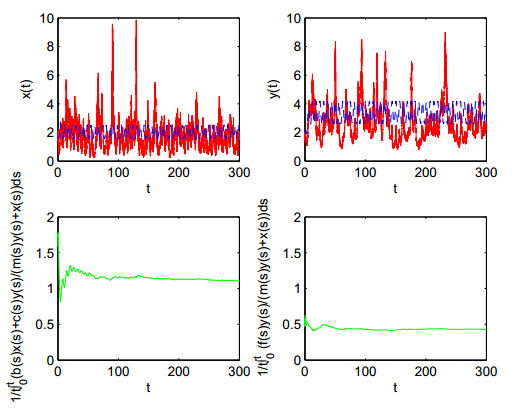
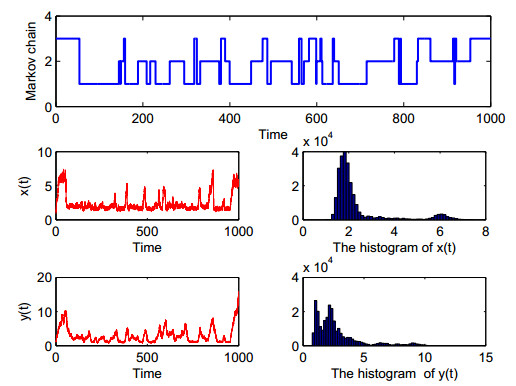
|
[1]
|
R. Arditi and L. R. Ginzburg, Coupling in predator-prey dynamics: ratiodependence, J. Theoret. Biol., 1989,139(3), 311-326. doi: 10.1016/S0022-5193(89)80211-5
CrossRef Google Scholar
|
|
[2]
|
R. Arditi, L. R. Ginzburg and H. R. Akcakaya, Variation in plankton densities among lakes: a case for ratio-dependent models, Am. Nat., 1991,138(5), 1287-1296. doi: 10.1086/285286
CrossRef Google Scholar
|
|
[3]
|
A. A. Berryman, The origins and evolution of predator-prey theory, Ecology, 1992, 73(5), 1530-1535. doi: 10.2307/1940005
CrossRef Google Scholar
|
|
[4]
|
F. Berezovskaya, G. Karev and R. Arditi, Parametric analysis of the ratiodependent predator-prey model, J. Math. Biol., 2001, 43(3), 221-246. doi: 10.1007/s002850000078
CrossRef Google Scholar
|
|
[5]
|
M. Bandyopadhyay and J. Chattopadhyay, Ratio-dependent predator-prey model: effect of environmental fluctuation and stability, Nonlinearity, 2005, 18(2), 913-936. doi: 10.1088/0951-7715/18/2/022
CrossRef Google Scholar
|
|
[6]
|
M. Bandyopadhyay and C. G. Chakrabarti, Deterministic and stochastic analysis of a nonlinear prey-predator system, J. Biol. Syst., 2003, 11(2), 161-172. doi: 10.1142/S0218339003000816
CrossRef Google Scholar
|
|
[7]
|
L. Bai, J. S. Li, K. Zhang and W. J. Zhao, Analysis of a stochastic ratiodependent predator-prey model driven by Lévy noise, Appl. Math. Comput., 2014,233(1), 480-493.
Google Scholar
|
|
[8]
|
J. M. Cushing, Periodic time-dependent predator-prey system, SIAM J. Appl. Math., 1977, 32(1), 82-95.
Google Scholar
|
|
[9]
|
J. Cui, Permanence of predator-prey system with periodic coefficients, Math. Comput. Modelling, 2005, 42(1-2), 87-98. doi: 10.1016/j.mcm.2005.03.001
CrossRef Google Scholar
|
|
[10]
|
J. Cui and Y. Takeuchi, Permanence, extinction and periodic solution of predator-prey system with Beddington-DeAngelis functional response, J. Math. Anal. Appl., 2006,317(2), 464-474. doi: 10.1016/j.jmaa.2005.10.011
CrossRef Google Scholar
|
|
[11]
|
N. H. Dang, N. H. Du and G. Yin, Existence of stationary distributions for Kolmogorov systems of competitive type under telegraph noise, J. Differential Equations, 2014,257(6), 2078-2101. doi: 10.1016/j.jde.2014.05.029
CrossRef Google Scholar
|
|
[12]
|
N. H. Du, N. H. Dang and N. T. Dieu, On stability in distribution of stochastic differential delay equations with Markovian switching, Systems Control Lett., 2014, 65(1), 43-49.
Google Scholar
|
|
[13]
|
H. I. Freedman, Deterministic Mathematical Models in Population Ecology, Marcel Dekker, New York, 1980.
Google Scholar
|
|
[14]
|
M. Fan, Q. Wang and X. Zou, Dynamics of a non-autonomous ratio-dependent predator-prey system, Proc. Roy. Soc. Edin-burgh Sect. A, 2003,133(1), 97-118. doi: 10.1017/S0308210500002304
CrossRef Google Scholar
|
|
[15]
|
G. Guo and J. Wu, The effect of mutual interference between predators on a predator-prey model with diffusion, J. Math. Anal. Appl., 2012,389(1), 179-194. doi: 10.1016/j.jmaa.2011.11.044
CrossRef Google Scholar
|
|
[16]
|
L. R. Ginzburg and H. R. Akcakaya, Consequences of ratio-dependent predation for steady state properties of ecosystems, Ecology, 1992, 73(5), 1536-1543. doi: 10.2307/1940006
CrossRef Google Scholar
|
|
[17]
|
I. Hanski, The functional response of predator: worries about scale, Trends Ecol. Evol., 1991, 6(5), 141-142. doi: 10.1016/0169-5347(91)90052-Y
CrossRef Google Scholar
|
|
[18]
|
S. B. Hsu, T. W. Hwang and Y. Kuang, Global analysis of the MichaelisMenten-type ratio-dependent predator-prey system, J. Math. Biol., 2001, 42(6), 489-506. doi: 10.1007/s002850100079
CrossRef Google Scholar
|
|
[19]
|
Q. X. Han and D. Q. Jiang, Periodic solution for stochastic non-autonomous multispecies Lotka-Volterra mutualism type ecosystem, Appl. Math. Comput., 2015,262(1), 204-217.
Google Scholar
|
|
[20]
|
K. Ioannis and E. S. Steven, Brownian Motion and Stochastic Calculus, second ed, Springer-Verlag, New York, 1991.
Google Scholar
|
|
[21]
|
M. Jovanovic and M. Krstic, Analysis of non-autonomous stochastic Gompertz model with delay, Appl. Math. Comput., 2014,242(1), 101-108.
Google Scholar
|
|
[22]
|
C. Y. Ji, D. Q. Jiang and X. Y. Li, Qualitative analysis of a stochastic ratiodependent predator-prey system, J. Comput. Appl. Math., 2001,235(5), 1326-1341.
Google Scholar
|
|
[23]
|
D. Jiang, N. Shi and X. Li, Global stability and stochastic permanence of a non-autonomous logistic equation with random perturbation, J. Math. Anal. Appl., 2008,340(1), 588-597. doi: 10.1016/j.jmaa.2007.08.014
CrossRef Google Scholar
|
|
[24]
|
Y. Kuang and E. Beretta, Global qualitative analysis of a ratio-dependent predator-prey system, J. Math. Biol., 1998, 36(4), 389-406. doi: 10.1007/s002850050105
CrossRef Google Scholar
|
|
[25]
|
B. Li and Y. Kuang, Heteroclinic bifercation in the Michaelis-Menten-type ratio-dependent predator-prey system, SIAM J. Appl. Math., 2007, 67(5), 1453-1464. doi: 10.1137/060662460
CrossRef Google Scholar
|
|
[26]
|
H. Y. Li and Z. K. She, Uniqueness of periodic solutions of a nonautonomous density-dependent predator-prey system, J. Math. Anal. Appl., 2015,422(2), 886-905. doi: 10.1016/j.jmaa.2014.09.008
CrossRef Google Scholar
|
|
[27]
|
M. Liu and K. Wang, The threshold between permanence and extinction for a stochastic logistic model with regime switching, J. Appl. Math. Comput., 2013, 43(1-2), 329-349. doi: 10.1007/s12190-013-0666-0
CrossRef Google Scholar
|
|
[28]
|
Q. Luo and X. Mao, Stochastic population dynamics under regime switching, J. Math. Anal. Appl., 2007,334(1), 69-84. doi: 10.1016/j.jmaa.2006.12.032
CrossRef Google Scholar
|
|
[29]
|
J. L. Lv and K. Wang, A stochastic ratio-dependent predator-prey model under regime switching, J. Inequal. Appl., 2011, 2011(1), 1-14.
Google Scholar
|
|
[30]
|
X. Mao, Stochastic Differential Equations and Applications, Horwood, New York, 1997.
Google Scholar
|
|
[31]
|
A. Settati and A. Lahrouz, Stationary distribution of stochastic population systems under regime switching, Appl. Math. Comput., 2014,244(1), 235-243.
Google Scholar
|
|
[32]
|
Y. Tang and W. Zhang, Heteroclinic bifurcation in a ratio-dependent predatorprey system, J. Math. Biol., 2005, 50(6), 699-712. doi: 10.1007/s00285-004-0307-1
CrossRef Google Scholar
|
|
[33]
|
M. Vasilova, Asymptotic behavior of a stochastic Gilpin-Ayala predator-prey system with time-dependent delay, Math. Comput. Model., 2013, 57(3-4), 764-781. doi: 10.1016/j.mcm.2012.09.002
CrossRef Google Scholar
|
|
[34]
|
Q. Wang, M. Fan and K. Wang, Dynamics of a class of nonautonomous semiratio-dependent predator-prey systems with functional responses, J. Math. Anal. Appl., 2003,278(2), 443-471. doi: 10.1016/S0022-247X(02)00718-7
CrossRef Google Scholar
|
|
[35]
|
D. Xiao and S. Ruan, Global dynamics of a ratio-dependent predator-prey system, J. Math. Biol., 2001, 43(3), 268-290. doi: 10.1007/s002850100097
CrossRef Google Scholar
|
|
[36]
|
A. Yagi and T. Viet Ton, Dynamic of a stochastic predator-prey population, Appl. Math. Comput., 2011,218(7), 3100-3109.
Google Scholar
|
|
[37]
|
J. Zhao and J. Jiang, Permanence in nonautonomous Lotka-Volterra system with predator-prey, Appl. Math. Comput., 2004,152(1), 99-109.
Google Scholar
|
|
[38]
|
L. Zu, D. Q. Jiang, D. O'Regan and B. Ge, Periodic solution for a nonautonomous Lotka-Volterra predator-prey model with random perturbation, J. Math. Anal. Appl., 2015,430(1), 428-437. doi: 10.1016/j.jmaa.2015.04.058
CrossRef Google Scholar
|
|
[39]
|
C. Zhu and G. Yin, Asymptotic properties of hybrid diffusion systems, SIAM J. Control Optim., 2007, 46(4), 1155-1179. doi: 10.1137/060649343
CrossRef Google Scholar
|




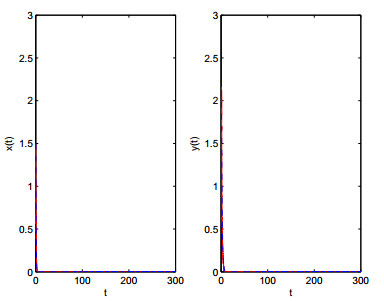

 DownLoad:
DownLoad: