| Citation: | Nolisa Malluwawadu, Saqib Hussain. A WEAK GALERKIN METHOD FOR SECOND ORDER ELLIPTIC PROBLEMS WITH POLYNOMIAL REDUCTION[J]. Journal of Applied Analysis & Computation, 2019, 9(2): 655-670. doi: 10.11948/2156-907X.20180137 |
A WEAK GALERKIN METHOD FOR SECOND ORDER ELLIPTIC PROBLEMS WITH POLYNOMIAL REDUCTION
-
Abstract
The second order elliptic equation, which is also know as the diffusion-convection equation, is of great interest in many branches of physics and industry. In this paper, we use the weak Galerkin finite element method to study the general second order elliptic equation. A weak Galerkin finite element method is proposed and analyzed. This scheme features piecewise polynomials of degree $k\geq 1$ on each element and piecewise polynomials of degree $k-1\geq 0$ on each edge or face of the element. Error estimates of optimal order of convergence rate are established in both discrete $H^1$ and standard $L^2$ norm. The paper also presents some numerical experiments to verify the efficiency of the method. -

-
References
[1] D. N. Arnold, An interior penalty finite element method with discontinuous elements, SIAM J. Numer. Anal., 1982, 19(4), 742-760. [2] D. Arnold, F. Brezzi, B. Cockburn, L. D. Marini, Unified analysis of discontinuous Galerkin methods for elliptic problems, SIAM J. Numer. Anal., 2002, 39, 1749-1779. doi: 10.1137/S0036142901384162 [3] K. Aziz, A. Settari, Petroleum Reservoir Simulations, Applied Science Publisher Ltd., London, 1979. [4] G. A. Baker, Finite Elements Methods for Elliptic equations using nonconforming elements, Math. Comp., 1977, 31, 45-59. doi: 10.1090/S0025-5718-1977-0431742-5 [5] C. E. Baumann, J. T. Oden, A discontinuous hp finite element method for convection-diffusion problems, Comput. Methods Appl. Mech. Engrg., 1999, 175, 311-341. doi: 10.1016/S0045-7825(98)00359-4 [6] J. Bear, Dynamics of Fluids in Porus Media, American Elsevier Publishing Company, New York, 1972. [7] S. Brenner, R. Scott, The mathematical theory of Finite Element Methods, Springer-verlag, New York, 1994. [8] F. Brezzi, K. Lipnikov, and M. Shashkov, Convergence of the mimetic finite difference method for diffusion problems on polyhedral meshes, SIAM J. Numer. Anal., 2005, 43(5), 1872-1896. doi: 10.1137/040613950 [9] P. G. Ciarlet, The finite element method for Elliptic Problems, Noth-Holland, New York, 1978. [10] L. Mu, J. Wang, X. Ye, A weak Galerkin finite element method with polynomial reduction, Journal of Computational and Applied Mathematics, 2015, 285, 45-58. arXiv:1304.6481v1. doi: 10.1016/j.cam.2015.02.001 [11] L. Mu, J. Wang, X. Ye, S. Zhao, A numerical study on the weak Galerkin method for the Helmholtz equation with large wave numbers, arXiv: 1111.0671v1, 2. [12] L. Mu, J. Wang, Y. Wang, X. Ye, A weak Galerkin mixed finite element method for biharmonic equations, Numerical Solution of Partial Differential Equations: Theory, Algorithms, and Their Applications, Springer Proceedings in Mathematics and Statistics, 2013, 45, 247-277. doi: 10.1007/978-1-4614-7172-1 [13] L. Mu, J. Wang, X. Ye, Weak Galerkin finite element methods for the biharmonic equation on polytopal meshes, Numerical Methods for PDEs, 2014, 30, 1003-1029. doi: 10.1002/num.v30.3 [14] L. Mu, J. Wang, X. Ye, S. Zhang, A weak Galerkin finite element method for the Maxwell equations, Journal of Scientific Computing, 2015, 65, 363-386. doi: 10.1007/s10915-014-9964-4 [15] L. Mu, J. Wang, X. Ye, S. Zhang, A $C^0$-weak Galerkin finite element method for the biharmonic equation, Journal of Scientific Computing, 2014, 59(2), 473-495. doi: 10.1007/s10915-013-9770-4 CrossRef $C^0$-weak Galerkin finite element method for the biharmonic equation" target="_blank">Google Scholar
[16] B. Riviere, M. F. Wheeler, V. Girault, A priori error estimate for finite element methods based on discontinuous approximation spaces for elliptic problems, SIAM J. Numer. Anal., 2001, 39, 902-931 doi: 10.1137/S003614290037174X [17] B. Riviere, M. F. Wheeler, V. Girault, Improved energy estimates for Interior Penalty, Constrained and Discontinuous Galerkin methods for Elliptic Problems. Part I, Computational Geosciences, 1999, 8, 337-360. [18] H. Wang, D. Liang, R. E. Ewing, S. L. Lyons, G. Qin, An Approximation to miscible fluid flows in pours media with point sources and sinks by an Eulerian-Lagrangian localized adjoint method and mixed finite element methods, SIAM Journal of Science and Computations, 2000, 22, 561-581. doi: 10.1137/S1064827598349215 [19] J. Wang, X. Ye, A weak Galerkin finite element method for second order elliptic problems, Journal of Computational and Applied Mathematics, 2013, 241, 103-115. arXiv:1104.2897v1. doi: 10.1016/j.cam.2012.10.003 [20] J. Wang, X. Ye, A weak Galerkin mixed finite element method for second order elliptic problems, arXiv: 1202.3655v2, 2012. [21] J. Wang, X. Ye, A weak Galerkin finite element method for the Stokes equation, arXiv: 1302.2707, 2013. [22] R. Zhang, Q. Zhai, A new weak Galerkin finite element scheme for the biharmonic equations by using polynomials of reduced order, J. Sci. Comput., 2015, 64(2), 559-585. -
-
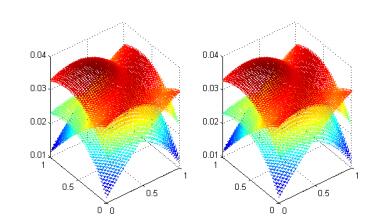
- Figure 1. Weak Galerkin Solution vs Exact Solution
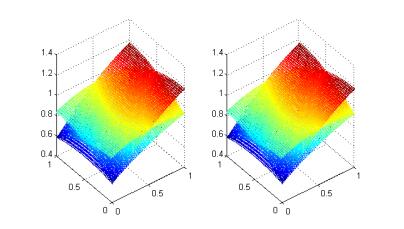
- Figure 2. Weak Galerkin Solution vs Exact Solution
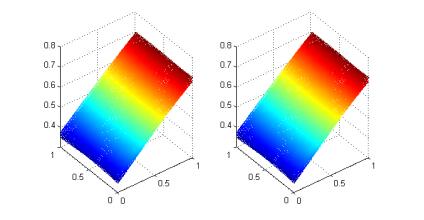
- Figure 3. Weak Galerkin Solution vs Exact Solution
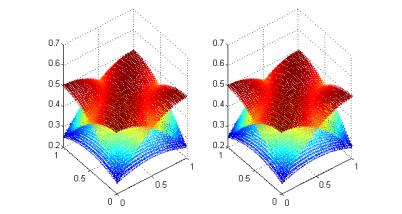
- Figure 4. Weak Galerkin Solution vs Exact Solution




 DownLoad:
DownLoad: