| Citation: |
R. Sivasamy, K. Sathiyanathan, K. Balachandran. DYNAMICS OF A MODIFIED LESLIE-GOWER MODEL WITH GESTATION EFFECT AND NONLINEAR HARVESTIN[J]. Journal of Applied Analysis & Computation, 2019, 9(2): 747-764. doi: 10.11948/2156-907X.20180165
|
DYNAMICS OF A MODIFIED LESLIE-GOWER MODEL WITH GESTATION EFFECT AND NONLINEAR HARVESTIN
-
Abstract
This study focuses on the dynamics of a modified Leslie-Gower predator-prey model where the intake rate of prey is by per capita predator according to Crowley-Martin functional response and prey is harvested through nonlinear harvesting strategy. Further the time-delay $(\tau)$ is imposed to utilize gestation period of predations. We investigate the permanence analysis of proposed system. The local stability of non-delayed model at all possible equilibrium points is studied. It is shown that the given model undergoes Hopf bifurcation around positive equilibrium point with respect to delay parameter $\tau$. Subsequently the stability of Hopf bifurcation and its direction are explored through normal and center manifold theories. The derived theoretical results are justified with the help of numerical simulations. -
-
References
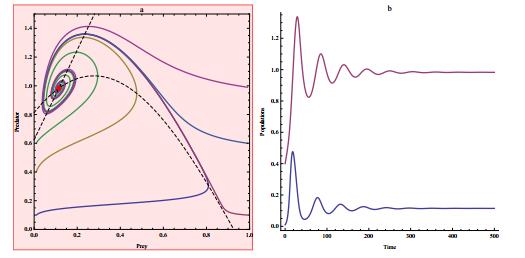
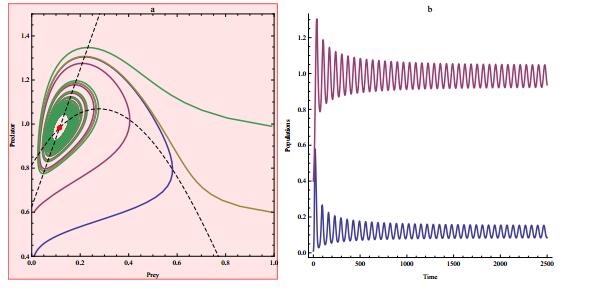
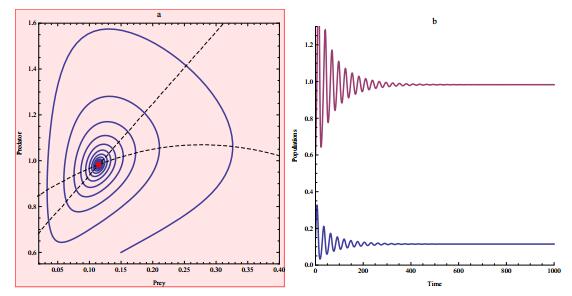
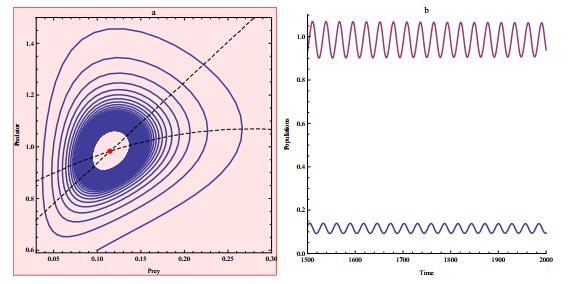
[1] N. Ali and M. Jazar, Global dynamics of a modified Leslie-Gower predator-prey model with Crowley-Martin functional responses, Journal of Applied Mathematics and Computing, 2013, 43(1-2), 271-293. doi: 10.1007/s12190-013-0663-3 [2] R. Arditi and L. R. Ginzburg, Coupling in predator-prey dynamics: ratio-dependence, Journal of theoretical biology, 1989, 139(3), 311-326. doi: 10.1016/S0022-5193(89)80211-5 [3] M. Aziz-Alaoui and M. Okiye, Boundedness and global stability for a predator-prey model with modified Leslie-Gower and Holling-type Ⅱ schemes, Applied Mathematics Letters, 2003, 16(7), 1069-1075. doi: 10.1016/S0893-9659(03)90096-6 [4] J. Beddington, Mutual interference between parasites or predators and its effect on searching efficiency, The Journal of Animal Ecology, 1975, 44(1), 331-340. [5] Q. Bie, Q. Wang and Z. Yao, Cross-diffusion induced instability and pattern formation for a Holling type-Ⅱ predator-prey model, Applied Mathematics and Computation, 2014, 247, 1-12. doi: 10.1016/j.amc.2014.08.088 [6] R. S. Cantrell and C. Cosner, On the dynamics of predator-prey models with the Beddington-DeAngelis functional response, Journal of Mathematical Analysis and Applications, 2001, 257(1), 206-222. [7] K. Chakraborty, S. Jana and T. Kar, Global dynamics and bifurcation in a stage structured prey-predator fishery model with harvesting, Applied Mathematics and Computation, 2012, 218(18), 9271-9290. doi: 10.1016/j.amc.2012.03.005 [8] L. Cheng and H. Cao, Bifurcation analysis of a discrete-time ratio-dependent predator-prey model with Allee effect, Communications in Nonlinear Science and Numerical Simulation, 2016, 38, 288-302. doi: 10.1016/j.cnsns.2016.02.038 [9] P. Crowley and E. Martin, Functional responses and interference within and between year classes of a dragonfly population, Journal of the North American Benthological Society, 1989, 8(3), 211-221. doi: 10.2307/1467324 [10] D. DeAngelis, R. Goldstein and R. O'neill, A model for tropic interaction, Ecology, 1975, 56(4), 881-892. doi: 10.2307/1936298 [11] R. Gupta and P. Chandra, Bifurcation analysis of modified Leslie-Gower predator-prey model with Michaelis-Menten type prey harvesting, Journal of Mathematical Analysis and Applications, 2013, 398(1), 278-295. [12] R. Gupta, P. Chandra and M. Banerjee, Dynamical complexity of a prey-predator model with nonlinear predator harvesting, Discrete and Continuous Dynamical Systems-Series B, 2015, 20(2), 423-443. doi: 10.3934/dcdsb [13] B. D. Hassard, N. D. Kazarinoff and Y.-H. Wan, Theory and applications of Hopf bifurcation, 41, Cambridge University Press Archive, 1981. [14] D. Hu and H. Cao, Stability and bifurcation analysis in a predator-prey system with Michaelis-Menten type predator harvesting, Nonlinear Analysis: Real World Applications, 2017, 33, 58-82. doi: 10.1016/j.nonrwa.2016.05.010 [15] J. Huang, Y. Gong and J. Chen, Multiple bifurcations in a predator-prey system of Holling and Leslie type with constant-yield prey harvesting, International Journal of Bifurcation and Chaos, 2013, 23(10), 1350164. doi: 10.1142/S0218127413501642 [16] J. Huang, S. Liu, S. Ruan and X. Zhang, Bogdanov-Takens bifurcation of codimension 3 in a predator-prey model with constant-yield predator harvesting, Communications on Pure and Applied Analysis, 2016, 15(3), 1041-1055. doi: 10.3934/cpaa [17] D. Jana, R. Pathak and M. Agarwal, On the stability and Hopf bifurcation of a prey-generalist predator system with independent age-selective harvesting, Chaos, Solitons & Fractals, 2016, 83, 252-273. [18] L. Ji and C. Wu, Qualitative analysis of a predator-prey model with constant-rate prey harvesting incorporating a constant prey refuge, Nonlinear Analysis: Real World Applications, 2010, 11(4), 2285-2295. doi: 10.1016/j.nonrwa.2009.07.003 [19] P. Leslie and J. Gower, The properties of a stochastic model for the predator-prey type of interaction between two species, Biometrika, 1960, 47(3/4), 219-234. doi: 10.2307/2333294 [20] Y. Li and C. Li, Stability and Hopf bifurcation analysis on a delayed Leslie-Gower predator-prey system incorporating a prey refuge, Applied Mathematics and Computation, 2013, 219(9), 4576-4589. doi: 10.1016/j.amc.2012.10.069 [21] H. Liu, T. Li and F. Zhang, A prey-predator model with Holling Ⅱ functional response and the carrying capacity of predator depending on its prey, Journal of Applied Analysis and Computation, 2018, 8(5), 1464-1474. [22] J. Liu and L. Zhang, Bifurcation analysis in a prey-predator model with nonlinear predator harvesting, Journal of the Franklin Institute, 2016, 353(17), 4701-4714. doi: 10.1016/j.jfranklin.2016.09.005 [23] P. Pal and P. Mandal, Bifurcation analysis of a modified Leslie-Gower predator-prey model with Beddington-DeAngelis functional response and strong Allee effect, Mathematics and Computers in Simulation, 2014, 97, 123-146. doi: 10.1016/j.matcom.2013.08.007 [24] P. J. Pal, P. K. Mandal and K. K. Lahiri, A delayed ratio-dependent predator-prey model of interacting populations with Holling type Ⅲ functional response, Nonlinear Dynamics, 2014, 76(1), 201-220. doi: 10.1007/s11071-013-1121-3 [25] M. Peng, Z. Zhang, X. Wang and X. Liu, Hopf bifurcation analysis for a delayed predator-prey system with a prey refuge and selective harvesting, Journal of Applied Analysis and Computation, 2018, 8(3), 982-997. [26] J. Ren, L. Yu and S. Siegmund, Bifurcations and chaos in a discrete predator-prey model with Crowley-Martin functional response, Nonlinear Dynamics, 2017, 90(1), 19-41. doi: 10.1007/s11071-017-3643-6 [27] B. Roy, S. K. Roy and D. B. Gurung, Holling-Tanner model with Beddington-DeAngelis functional response and time delay introducing harvesting, Mathematics and Computers in Simulation, 2017, 142, 1-14. doi: 10.1016/j.matcom.2017.03.010 [28] T. Saha and C. Chakrabarti, Dynamical analysis of a delayed ratio-dependent Holling-Tanner predator-prey model, Journal of Mathematical Analysis and Applications, 2009, 358(2), 389-402. [29] Y. Song and J. Wei, Local Hopf bifurcation and global periodic solutions in a delayed predator-prey system, Journal of Mathematical Analysis and Applications, 2005, 301(1), 1-21. [30] R. Yang and C. Zhang, Dynamics in a diffusive modified Leslie-Gower predator-prey model with time delay and prey harvesting, Nonlinear Dynamics, 2017, 87(2), 863-878. doi: 10.1007/s11071-016-3084-7 [31] H. Yin, X. Xiao, X. Wen and K. Liu, Pattern analysis of a modified Leslie-Gower predator-prey model with Crowley-Martin functional response and diffusion, Computers & Mathematics with Applications, 2014, 67(8), 1607-1621. [32] R. Yuan, W. Jiang and Y. Wang, Saddle-node-Hopf bifurcation in a modified Leslie-Gower predator-prey model with time-delay and prey harvesting, Journal of Mathematical Analysis and Applications, 2015, 422(2), 1072-1090. doi: 10.1016/j.jmaa.2014.09.037 [33] S. Yuan and Y. Song, Bifurcation and stability analysis for a delayed Leslie-Gower predator-prey system, IMA Journal of Applied Mathematics, 2009, 74(4), 574-603. doi: 10.1093/imamat/hxp013 [34] J. Zhou, Qualitative analysis of a modified Leslie-Gower predator-prey model with Crowley-Martin functional responses, Communications on Pure and Applied Analysis, 2015, 14(3), 1127-1145. doi: 10.3934/cpaa -
-
Figures(5)
Export File
Citation
R. Sivasamy, K. Sathiyanathan, K. Balachandran. DYNAMICS OF A MODIFIED LESLIE-GOWER MODEL WITH GESTATION EFFECT AND NONLINEAR HARVESTIN[J]. Journal of Applied Analysis & Computation, 2019, 9(2): 747-764. doi: 10.11948/2156-907X.20180165
Format
Content
DownLoad:
- Figure 1. The existence of all possible equilibrium points (red bullets)
-
Figure 2. (a) The phase space diagram of (5.1) for
$ \gamma = 0.1 $ . (b) The time trajectories of system (5.1) for$ \gamma = 0.1 $ . Thus$ E_* = (0.114545, 0.982954) $ is locally asymptotically stable -
Figure 3. (a) The phase space diagram of (5.1) for
$ \gamma=0.07 $ . (b) The time trajectories of system (5.1) for$ \gamma=0.07 $ . Thus the model (5.1) undergoes Hopf bifurcation around$ E_*. $ -
Figure 4. (a) The phase space diagram of (5.2) for
$ \tau = 3.0 $ . (b) The time trajectories of system (5.2) for$ \tau = 3.0 $ . Thus$ E_* $ is locally asymptotically stable -
Figure 5. (a) The phase space diagram of (5.2) for
$ \tau = 3.27 $ . (b) The periodic solutions of system (5.2) for$ \tau = 3.27 $ . Thus the model (5.2) undergoes Hopf bifurcation around$ E_*. $