| Citation: | Wen-Xiu Ma. A SEARCH FOR LUMP SOLUTIONS TO A COMBINED FOURTH-ORDER NONLINEAR PDE IN (2+1)-DIMENSIONS[J]. Journal of Applied Analysis & Computation, 2019, 9(4): 1319-1332. doi: 10.11948/2156-907X.20180227 |
A SEARCH FOR LUMP SOLUTIONS TO A COMBINED FOURTH-ORDER NONLINEAR PDE IN (2+1)-DIMENSIONS
-
Abstract
We aim to explore new (2+1)-dimensional nonlinear equations which possess lump solutions. Through the Hirota bilinear method, we formulate a combined fourth-order nonlinear equation while guaranteeing the existence of lump solutions. The class of lump solutions is constructed explicitly in terms of the coefficients of the combined nonlinear equation via symbolic computations. Specific examples are discussed to show the richness of the considered combined nonlinear equation. Three dimensional plots and contour plots of specific lump solutions to two specially chosen cases of the equation are made to shed light on the presented lump solutions.-
Keywords:
- Lump solution /
- Hirota bilinear method /
- integrable equation /
- symbolic computation /
- soliton
-

-
References
[1] M. J. Ablowitz and H. Segur, Solitons and the Inverse Scattering Transform, SIAM, Philadelphia, 1981. [2] P. J. Caudrey, Memories of Hirota's method: application to the reduced Maxwell-Bloch system in the early 1970s, Phil. Trans. R. Soc. A, 2011, 369(1939), 1215-1227. doi: 10.1098/rsta.2010.0337 [3] S. T. Chen and W. X. Ma, Lumps solutions to a generalized Calogero-Bogoyavlenskii-Schiff equation, Comput. Math. Appl., 2018, 76(7), 1680-1685. doi: 10.1016/j.camwa.2018.07.019 [4] S. T. Chen and W. X. Ma, Lump solutions to a generalized Bogoyavlensky-Konopelchenko equation, Front. Math. China, 2018, 13(3), 525-534. doi: 10.1007/s11464-018-0694-z [5] H. H. Dong, Y. Zhang and X. E. Zhang, The new integrable symplectic map and the symmetry of integrable nonlinear lattice equation, Commun. Nonlinear Sci. Numer. Simulat., 2016, 36, 354-365. doi: 10.1016/j.cnsns.2015.12.015 [6] B. Dorizzi, B. Grammaticos, A. Ramani and P. Winternitz, Are all the equations of the Kadomtsev-Petviashvili hierarchy integrable? J. Math. Phys., 1986, 27(12), 2848-2852. doi: 10.1063/1.527260 [7] L. N. Gao, Y. Y. Zi, Y. H. Yin, W. X. Ma and X. Lü, Bäcklund transformation, multiple wave solutions and lump solutions to a (3+1)-dimensional nonlinear evolution equation, Nonlinear Dynam., 2017, 89(3), 2233-2240. doi: 10.1007/s11071-017-3581-3 [8] C. R. Gilson and J. J. C. Nimmo, Lump solutions of the BKP equation, Phys. Lett. A, 1990, 147(8-9), 472-476. doi: 10.1016/0375-9601(90)90609-R [9] Harun-Or-Roshid and M. Z. Ali, Lump solutions to a Jimbo-Miwa like equation, 2016, arXiv: 1611.04478. [10] J. Hietarinta, Introduction to the Hirota bilinear method, in: Integrability of Nonlinear Systems, Y. Kosmann-Schwarzbach, B. Grammaticos and K. M. Tamizhmani (Eds.), pp. 95-103, Springer, Berlin, Heidelberg, 1997. [11] R. Hirota, The Direct Method in Soliton Theory, Cambridge University Press, New York, 2004. [12] N. H. Ibragimov, A new conservation theorem, J. Math. Anal. Appl., 2007, 333(1), 311-328. doi: 10.1016/j.jmaa.2006.10.078 [13] K. Imai, Dromion and lump solutions of the Ishimori-Ⅰ equation, Prog. Theor. Phys., 1997, 98(5), 1013-1023. doi: 10.1143/PTP.98.1013 [14] D. J. Kaup, The lump solutions and the Bäcklund transformation for the three-dimensional three-wave resonant interaction, J. Math. Phys., 1981, 22(6), 1176-1181. doi: 10.1063/1.525042 [15] T. C. Kofane, M. Fokou, A. Mohamadou and E. Yomba, Lump solutions and interaction phenomenon to the third-order nonlinear evolution equation, Eur. Phys. J. Plus, 2017, 132, 465. doi: 10.1140/epjp/i2017-11747-6 [16] B. Konopelchenko and W. Strampp, The AKNS hierarchy as symmetry constraint of the KP hierarchy, Inverse Probl., 1991, 7(2), L17-L24. doi: 10.1088/0266-5611/7/2/002 [17] X. Y. Li and Q. L. Zhao, A new integrable symplectic map by the binary nonlinearization to the super AKNS system, J. Geom. Phys., 2017, 121, 123-137. doi: 10.1016/j.geomphys.2017.07.010 [18] X. Y. Li, Q. L. Zhao, Y. X. Li and H. H. Dong, Binary Bargmann symmetry constraint associated with 3× discrete matrix spectral problem, J. Nonlinear Sci. Appl., 2015, 8, 496-506. doi: 10.22436/jnsa [19] J. G. Liu, L. Zhou and Y. He, Multiple soliton solutions for the new (2+1)-dimensional Korteweg-de Vries equation by multiple exp-function method, Appl. Math. Lett., 2018, 80, 71-78. doi: 10.1016/j.aml.2018.01.010 [20] X. Lü, S. T. Chen and W. X. Ma, Constructing lump solutions to a generalized Kadomtsev-Petviashvili-Boussinesq equation, Nonlinear Dynam., 2016, 86(1), 523-534. doi: 10.1007/s11071-016-2905-z [21] X. Lü, W. X. Ma, S. T. Chen and C. M. Khalique, A note on rational solutions to a Hirota-Satsuma-like equation, Appl. Math. Lett., 2016, 58, 13-18. doi: 10.1016/j.aml.2015.12.019 [22] X. Lü, W. X. Ma, Y. Zhou and C. M. Khalique, Rational solutions to an extended Kadomtsev-Petviashvili like equation with symbolic computation, Comput. Math. Appl., 2016, 71(8), 1560-1567. doi: 10.1016/j.camwa.2016.02.017 [23] W. X. Ma, Lump solutions to the Kadomtsev-Petviashvili equation, Phys. Lett. A, 2015, 379(36), 1975-1978. doi: 10.1016/j.physleta.2015.06.061 [24] W. X. Ma, Conservation laws of discrete evolution equations by symmetries and adjoint symmetries, Symmetry, 2015, 7(2), 714-725. doi: 10.3390/sym7020714 [25] W. X. Ma, Lump-type solutions to the (3+1)-dimensional Jimbo-Miwa equation, Int. J. Nonlinear Sci. Numer. Simulat., 2016, 17, 355-359. [26] W. X. Ma, Conservation laws by symmetries and adjoint symmetries, Discrete Contin. Dyn. Syst. Series S, 2018, 11(4), 707-721. [27] W. X. Ma, Riemann-Hilbert problems and $N$-soliton solutions for a coupled mKdV system, J. Geom. Phys., 2018, 132, 45-54. doi: 10.1016/j.geomphys.2018.05.024 CrossRef $N$-soliton solutions for a coupled mKdV system" target="_blank">Google Scholar
[28] W. X. Ma, Abundant lumps and their interaction solutions of (3+1)-dimensional linear PDEs, J. Geom. Phys., 2018, 133, 10-16. doi: 10.1016/j.geomphys.2018.07.003 [29] W. X. Ma, Lump and interaction solutions of linear PDEs in (3+1)-dimensions, East Asian J. Appl. Math., 2019, 9(1), 185-194. doi: 10.4208/eajam.100218.300318 [30] W. X. Ma and E. G. Fan, Linear superposition principle applying to Hirota bilinear equations, Comput. Math. Appl., 2011, 61(4), 950-959. doi: 10.1016/j.camwa.2010.12.043 [31] W. X. Ma, J. Li and C. M. Khalique, A study on lump solutions to a generalized Hirota-Satsuma-Ito equation in (2+1)-dimensions, Complexity, 2018, 2018, Article ID 9059858, 7 pp. [32] W. X. Ma, Z. Y. Qin and X. Lü, Lump solutions to dimensionally reduced p-gKP and p-gBKP equations, Nonlinear Dynam., 2016, 84(2), 923-931. doi: 10.1007/s11071-015-2539-6 [33] W. X. Ma and W. Strampp, An explicit symmetry constraint for the Lax pairs and the adjoint Lax pairs of AKNS systems, Phys. Lett. A, 1994, 185(3), 277-286. doi: 10.1016/0375-9601(94)90616-5 [34] W. X. Ma, X. L. Yong and H. Q. Zhang, Diversity of interaction solutions to the (2+1)-dimensional Ito equation, Comput. Math. Appl., 2018, 75(1), 289-295. doi: 10.1016/j.camwa.2017.09.013 [35] W. X. Ma and Y. Zhou, Lump solutions to nonlinear partial differential equations via Hirota bilinear forms, J. Diff. Eqns., 2018, 264(4), 2633-2659. doi: 10.1016/j.jde.2017.10.033 [36] W. X. Ma, Y. Zhou and R. Dougherty, Lump-type solutions to nonlinear differential equations derived from generalized bilinear equations, Int. J. Mod. Phys. B, 2016, 30(28n29), 1640018. doi: 10.1142/S021797921640018X [37] S. V. Manakov, V. E. Zakharov, L. A. Bordag and V. B. Matveev, Two-dimensional solitons of the Kadomtsev-Petviashvili equation and their interaction, Phys. Lett. A, 1977, 63(3), 205-206. doi: 10.1016/0375-9601(77)90875-1 [38] S. Manukure, Y. Zhou and W. X. Ma, Lump solutions to a (2+1)-dimensional extended KP equation, Comput. Math. Appl., 2018, 75(7), 2414-2419. doi: 10.1016/j.camwa.2017.12.030 [39] S. Novikov, S. V. Manakov, L. P. Pitaevskii and V. E. Zakharov, Theory of Solitons - The Inverse Scattering Method, Consultants Bureau, New York, 1984. [40] J. Satsuma and M. J. Ablowitz, Two-dimensional lumps in nonlinear dispersive systems, J. Math. Phys., 1979, 20(7), 1496-1503. doi: 10.1063/1.524208 [41] Y. Sun, B. Tian, X. Y. Xie, J. Chai and H. M. Yin, Rogue waves and lump solitons for a (3+1)-dimensional B-type Kadomtsev-Petviashvili equation in fluid dynamics, Wave Random Complex, 2018, 28(3), 544-552. doi: 10.1080/17455030.2017.1367866 [42] W. Tan, H. P. Dai, Z. D. Dai and W. Y. Zhong, Emergence and space-time structure of lump solution to the (2+1)-dimensional generalized KP equation, Pramana - J. Phys., 2017, 89, 77. doi: 10.1007/s12043-017-1474-0 [43] Y. N. Tang, S. Q. Tao and G. Qing, Lump solitons and the interaction phenomena of them for two classes of nonlinear evolution equations, Comput. Math. Appl., 2016, 72(9), 2334-2342. doi: 10.1016/j.camwa.2016.08.027 [44] Ö. Ünsal and W. X. Ma, Linear superposition principle of hyperbolic and trigonometric function solutions to generalized bilinear equations, Comput. Math. Appl., 2016, 71(6), 1242-1247. doi: 10.1016/j.camwa.2016.02.006 [45] H. Wang, Lump and interaction solutions to the (2+1)-dimensional Burgers equation, Appl. Math. Lett., 2018, 85, 27-34. doi: 10.1016/j.aml.2018.05.010 [46] D. S. Wang and Y. B. Yin, Symmetry analysis and reductions of the two-dimensional generalized Benney system via geometric approach, Comput. Math. Appl., 2016, 71(3), 748-757. doi: 10.1016/j.camwa.2015.12.035 [47] J. P. Wu and X. G. Geng, Novel Wronskian condition and new exact solutions to a (3+1)-dimensional generalized KP equation, Commun. Theoret. Phys., 2013, 60(5), 556-510. doi: 10.1088/0253-6102/60/5/08 [48] X. X. Xu, A deformed reduced semi-discrete Kaup-Newell equation, the related integrable family and Darboux transformation, Appl. Math. Comput., 2015, 251, 275-283. [49] Z. H. Xu, H. L. Chen and Z. D. Dai, Rogue wave for the (2+1)-dimensional Kadomtsev-Petviashvili equation, Appl. Math. Lett., 2014, 37, 34-38. doi: 10.1016/j.aml.2014.05.005 [50] X. X. Xu and M. Xu, A family of integrable different-difference equations, its Hamiltonian structure, and Darboux-Bäcklund transformation, Discrete Dyn. Nat. Soc., 2018, 2018 Art. ID 4152917, 11 pp. [51] J. Y. Yang and W. X. Ma, Lump solutions of the BKP equation by symbolic computation, Int. J. Mod. Phys. B, 2016, 30(28n29), 1640028. doi: 10.1142/S0217979216400282 [52] J. Y. Yang and W. X. Ma, Abundant lump-type solutions of the Jimbo-Miwa equation in (3+1)-dimensions, Comput. Math. Appl., 2017, 73(2), 220-225. doi: 10.1016/j.camwa.2016.11.007 [53] J. Y. Yang and W. X. Ma, Abundant interaction solutions of the KP equation, Nonlinear Dynam., 2017, 89(2), 1539-1544. doi: 10.1007/s11071-017-3533-y [54] J. Y. Yang, W. X. Ma and Z. Y. Qin, Lump and lump-soliton solutions to the (2+1)-dimensional Ito equation, Anal. Math. Phys., 2018, 8(3), 427-436. doi: 10.1007/s13324-017-0181-9 [55] J. Y. Yang, W. X. Ma and Z. Y. Qin, Abundant mixed lump-soliton solutions to the BKP equation, East Asian J. Appl. Math., 2018, 8(2), 224-232. doi: 10.4208/eajam.210917.051217a [56] Y. H. Yin, W. X. Ma, J. G. Liu and X. Lü, Diversity of exact solutions to a (3+1)-dimensional nonlinear evolution equation and its reduction, Comput. Math. Appl., 2018, 76(6), 1225-1283. [57] X. L. Yong, W. X. Ma, Y. H. Huang and Y. Liu, Lump solutions to the Kadomtsev-Petviashvili I equation with a self-consistent source, Comput. Math. Appl., 2018, 75(9), 3414-3419. doi: 10.1016/j.camwa.2018.02.007 [58] J. P. Yu and Y. L. Sun, Study of lump solutions to dimensionally reduced generalized KP equations, Nonlinear Dynam., 2017, 87(4), 2755-2763. doi: 10.1007/s11071-016-3225-z [59] H. C. Zheng, W. X. Ma and X. Gu, Hirota bilinear equations with linear subspaces of hyperbolic and trigonometric function solutions, Appl. Math. Comput., 2013, 220, 226-234. [60] X. E. Zhang, Y. Chen and Y. Zhang, Breather, lump and soliton solutions to nonlocal KP equation, Comput. Math. Appl., 2017, 74(10), 2341-2347. doi: 10.1016/j.camwa.2017.07.004 [61] Y. Zhang, H. H. Dong, X. E. Zhang and H. W. Yang, Rational solutions and lump solutions to the generalized (3 + 1)-dimensional shallow water-like equation, Comput. Math. Appl., 2017, 73(2), 246-252. doi: 10.1016/j.camwa.2016.11.009 [62] Y. Zhang, Y. P. Liu and X. Y. Tang, $M$-lump solutions to a (3+1)-dimensional nonlinear evolution equation, Comput. Math. Appl., 2018, 76(3), 592-601. doi: 10.1016/j.camwa.2018.04.039 CrossRef $M$-lump solutions to a (3+1)-dimensional nonlinear evolution equation" target="_blank">Google Scholar
[63] Y. Zhang, S. L. Sun and H. H. Dong, Hybrid solutions of (3+1)-dimensional Jimbo-Miwa equation, Math. Probl. Eng., 2017, 2017, Article ID 5453941, 15 pp. [64] H. Q. Zhang and W. X. Ma, Lump solutions to the (2+1)-dimensional Sawada-Kotera equation, Nonlinear Dynam., 2017, 87(4), 2305-2310. doi: 10.1007/s11071-016-3190-6 [65] J. B. Zhang and W. X. Ma, Mixed lump-kink solutions to the BKP equation, Comput. Math. Appl., 2017, 74(3), 591-596. doi: 10.1016/j.camwa.2017.05.010 [66] Q. L. Zhao and X. Y. Li, A Bargmann system and the involutive solutions associated with a new 4-order lattice hierarchy, Anal. Math. Phys., 2016, 6(3), 237-254. doi: 10.1007/s13324-015-0116-2 [67] H. Q. Zhao and W. X. Ma, Mixed lump-kink solutions to the KP equation, Comput. Math. Appl., 2017, 74(6), 1399-1405. doi: 10.1016/j.camwa.2017.06.034 [68] Y. Zhou and W. X. Ma, Applications of linear superposition principle to resonant solitons and complexitons, Comput. Math. Appl., 2017, 73(8), 1697-1706. doi: 10.1016/j.camwa.2017.02.015 [69] Y. Zhou, S. Manukure and W. X. Ma, Lump and lump-soliton solutions to the Hirota-Satsuma-Ito equation, Commun. Nonlinear Sci. Numer. Simulat., 2019, 68, 56-62. doi: 10.1016/j.cnsns.2018.07.038 -
-
-
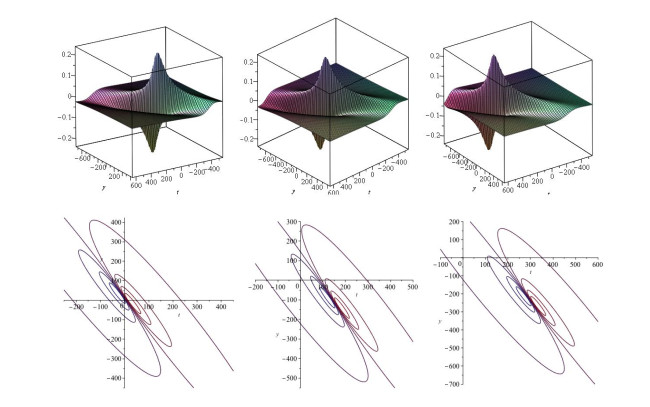
Figure 1. Profiles of
$ u_1 $ when$ t = 0, 15, 30 $ : 3d plots (top) and contour plots (bottom) -
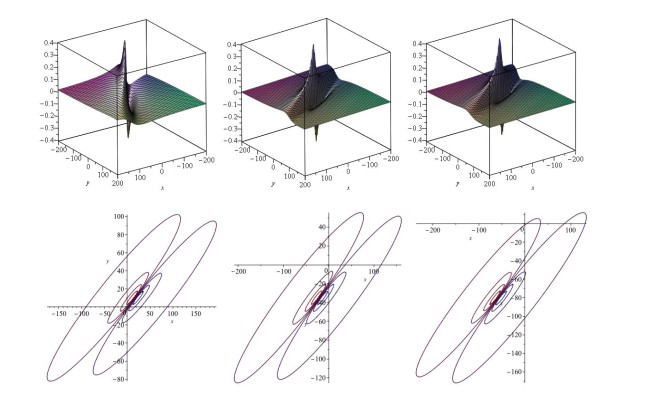
Figure 2. Profiles of
$ u_2 $ when$ t = 0, 50, 100 $ : 3d plots (top) and contour plots (bottom)




 DownLoad:
DownLoad: