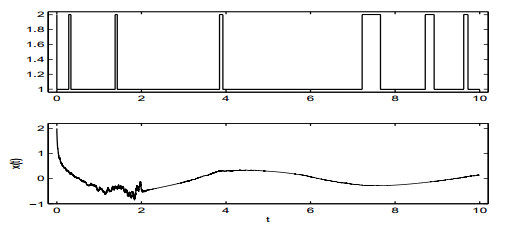
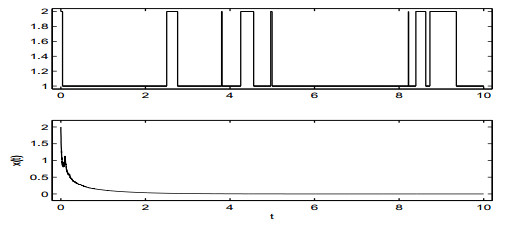
|
[1]
|
A. Ahlborn and U. Parlitz, Stabilizing unstable steady states using multiple delay feedback control, Phys. Rev. Lett., 2014, 93, 264101.
Google Scholar
|
|
[2]
|
C. Briat, Stability analysis and stabilization of stochastic linear impulsive, switched and sampled-data systems under dwell-time constraints, Automatica, 2016, 74, 279-287. doi: 10.1016/j.automatica.2016.08.001
CrossRef Google Scholar
|
|
[3]
|
H. B. Chen, P. Shi and C. Lim, Stability analysis for neutral stochastic delay systems with Markovian switching, Syst. Control Lett., 2017, 110, 38-48. doi: 10.1016/j.sysconle.2017.10.008
CrossRef Google Scholar
|
|
[4]
|
V. Dragan and H. Mukaidani, Exponential stability in mean square of a singularly perturbed linear stochastic system with state-multiplicative white-noise perturbations and Markovian switching, IET Control Theory Appl., 2016, 9, 1040-1051.
Google Scholar
|
|
[5]
|
C. Fei, W. Y. Fei and L. T. Yan, Existence and stability of solutions to highly nonlinear stochastic differential delay equations driven by G-Brownian motion, Appl. Math. J. Chinese Univ., to appear.
Google Scholar
|
|
[6]
|
C. Fei, M. X. Shen, W. Y. Fei, X. R. Mao and L. T. Yan, Stability of highly nonlinear hybrid stochastic integro-differential delay equations, Nonlinear Anal. Hybrid Syst., 2019, 31, 180-199. doi: 10.1016/j.nahs.2018.09.001
CrossRef Google Scholar
|
|
[7]
|
W. Y. Fei, L. J. Hu, X. M. Mao and M. X. Shen, Delay dependent stability of highly nonlinear hybrid stochastic systems, Automatica, 2017, 28, 165-170.
Google Scholar
|
|
[8]
|
W. Y. Fei, L. J. Hu, X. R. Mao and M. X. Shen, Structured robust stability and boundedness of nonlinear hybrid delay systems, SIAM J. Control Optim., 2018, 56, 2662-2689. doi: 10.1137/17M1146981
CrossRef Google Scholar
|
|
[9]
|
W. Y. Fei, L. J. Hu, X. R. Mao and M. X. Shen, Generalised criteria on delay dependent stability of highly nonlinear hybrid stochastic systems, Int. J. Robust. Nonlin., 2019, 25, 1201-1215.
Google Scholar
|
|
[10]
|
M. Frederic, Stability analysis of time-varying neutral time-delay systems, IEEE Trans. Automat. Control, 2016, 60, 540-546.
Google Scholar
|
|
[11]
|
E. Fridman, Introduction to Time-Delay Systems: Analysis and Control, Birkhauser, 2014.
Google Scholar
|
|
[12]
|
A. Garab, V. Kovács and T. Krisztin Global stability of a price model with multiple delays, Discrete Contin. Dyn. Syst. A., 2016, 36(12), 6855-6871. doi: 10.3934/dcdsa
CrossRef Google Scholar
|
|
[13]
|
J. K. Hale and S. M. Lunel, Introduction to Functional Differential Equations, Springer-Verlag, 1993.
Google Scholar
|
|
[14]
|
L. J. Hu, X. R. Mao and Y. Shen, Stability and boundedness of nonlinear hybrid stochastic differential delay equations, Syst. Control Lett., 2013, 62, 178-187. doi: 10.1016/j.sysconle.2012.11.009
CrossRef Google Scholar
|
|
[15]
|
L. J. Hu, X. R. Mao and L. G. Zhang, Robust stability and boundedness of nonlinear hybrid stochastic delay equations, IEEE Trans. Automat Control, 2013, 58(9), 2319-2332. doi: 10.1109/TAC.2013.2256014
CrossRef Google Scholar
|
|
[16]
|
V. B. Kolmanovskii and V. R. Nosov, Stability of Functional Differential Equations, Academic Press, London, 1986.
Google Scholar
|
|
[17]
|
M. L. Li and M. C. Huang, Approximate controllability of second-order impulsive stochastic differential equations with state-dependent delay, J. Appl. Anal. Comput., 2018, 8(2), 598-619.
Google Scholar
|
|
[18]
|
X. D. Li, Q. X. Zhu and D. O'Reganc, pth Moment exponential stability of impulsive stochastic functional differential equations and application to control problems of NNs, J. Franklin Inst., 2014, 351, 4435-4456. doi: 10.1016/j.jfranklin.2014.04.008
CrossRef Google Scholar
|
|
[19]
|
J. Lei and M. Mackey, Stochastic differential delay equation, moment stability, and application to hematopoitic stem cell regulation systems, SIAM J. Appl. Math., 2007, 67(2), 387-407. doi: 10.1137/060650234
CrossRef Google Scholar
|
|
[20]
|
J. Liu, On asymptotic convergence and boundedness of stochastic systems with time-delay, Automatica, 2012, 48, 3166-3172. doi: 10.1016/j.automatica.2012.08.041
CrossRef Google Scholar
|
|
[21]
|
K. Liu, Almost sure exponential stability sensitive to small time delay of stochastic neutral functional differential equations, Appl. Math. Lett., 2018, 77, 57-63. doi: 10.1016/j.aml.2017.09.008
CrossRef Google Scholar
|
|
[22]
|
X. R. Mao, Razumikhin-type theorems on exponential stability of stochastic functional differential eqautions, Stoch. Process. Appl., 1996, 65, 233-250. doi: 10.1016/S0304-4149(96)00109-3
CrossRef Google Scholar
|
|
[23]
|
X. R. Mao, Exponential stability of stochastic delay interval systems with Markovian switching, IEEE Trans. Auto. Control, 2002, 47(10), 1604-1612. doi: 10.1109/TAC.2002.803529
CrossRef Google Scholar
|
|
[24]
|
X. R. Mao, Stochastic Differential Equations and Their Applications, 2nd Edition, Chichester: Horwood Pub., 2007.
Google Scholar
|
|
[25]
|
X. R. Mao, J. Lam, and L. R. Huang, Stabilisation of hybrid stochastic differential equations by delay feedback control, Syst. Control Lett., 2008, 57, 927-935. doi: 10.1016/j.sysconle.2008.05.002
CrossRef Google Scholar
|
|
[26]
|
X. R. Mao and C. G. Yuan, Stochastic Differential Equations with Markovian Switching, Imperial College Press, 2006.
Google Scholar
|
|
[27]
|
S. E. A. Mohammed, Stochastic Functional Differential Equations, Longman Scientific and Technical, 1984.
Google Scholar
|
|
[28]
|
C. Park, N. Kwon and P. Park, Optimal H∞ filtering for singular Markovian jump systems, Syst. Control Lett., 2018, 118, 22-28. doi: 10.1016/j.sysconle.2018.05.005
CrossRef Google Scholar
|
|
[29]
|
A. Rathinasamy and M. Balachandran, Mean-square stability of semi-implicit Euler method for linear stochastic differential equations with multiple delays and Markovian switching, Appl. Math. Comput., 2008, 206, 968-979.
Google Scholar
|
|
[30]
|
M. X. Shen, C. Fei, W. Y. Fei and X. R. Mao, The boundedness and stability of highly nonlinear hybrid neutral stochastic systems with multiple delays, Sci. China Inf. Sci., DOI: 10.1007/s11432-018-9755-7.
Google Scholar
|
|
[31]
|
M. X. Shen, W. Y. Fei, X. R. Mao and S. N. Deng, Exponential stability of highly nonlinear neutral pantograph stochastic differential equations, Asian J. Control, DOI: 10.1002/asjc.1903.
Google Scholar
|
|
[32]
|
M. X. Shen, W. Y. Fei, X. R. Mao and Y. Liang, Stability of highly nonlinear neutral stochastic differential delay equations, Syst. Control Lett., 2018, 115, 1-8. doi: 10.1016/j.sysconle.2018.02.013
CrossRef Google Scholar
|
|
[33]
|
S. Y. Xu, J. Lam and X. R. Mao, Delay-dependent H∞ control and filtering for uncertain Markovian jump systems with time-varying delays, IEEE Trans. Circuits Syst. I, 2007, 54(9), 2070-2077. doi: 10.1109/TCSI.2007.904640
CrossRef Google Scholar
|
|
[34]
|
S. R. You, W. Liu, J. Q. Lu, X. R. Mao and J. W. Qiu, Stablization of hybrid systems by feedback control based on discrete-time state observation, SIAM J. Contrl Optim., 2015, 53(2), 905-925. doi: 10.1137/140985779
CrossRef Google Scholar
|
|
[35]
|
D. Yue and Q. Han, Delay-dependent exponential stability of stochastic systems with time-varying delay, nonlinearity, and Markovian switching, IEEE Trans. Automat. Control, 2005, 50, 217-222. doi: 10.1109/TAC.2004.841935
CrossRef Google Scholar
|
|
[36]
|
Q. X. Zhu, Stability analysis of stochastic delay differential equations with Lévy noise, Syst. Control Lett., 2018, 118, 62-68. doi: 10.1016/j.sysconle.2018.05.015
CrossRef Google Scholar
|




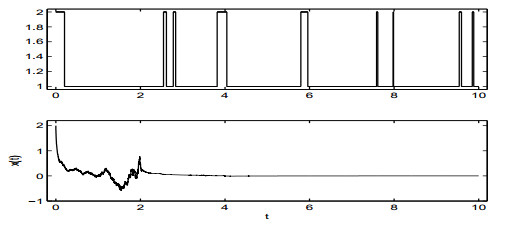

 DownLoad:
DownLoad: