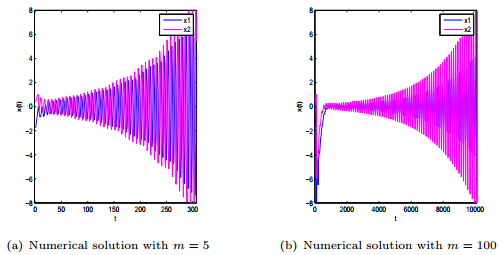
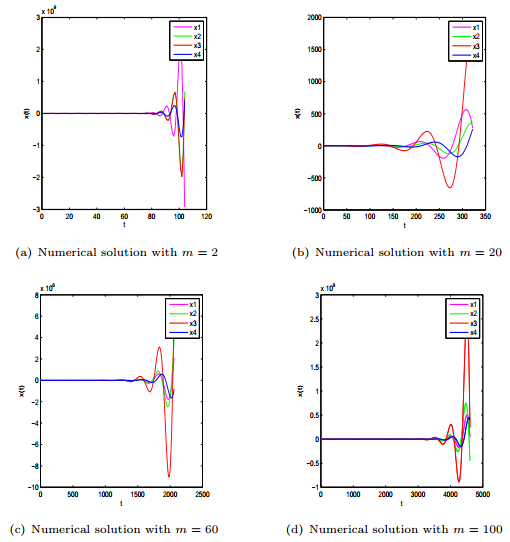
|
[1]
|
A. Bellen, N. Guglielmi and M. Zennaro, Numerical stability of nonlinear delay differential equations of neutral type, J. Comput. Appl. Math., 2000,125,251-263.
Google Scholar
|
|
[2]
|
A. Bellen and M. Zennaro, Numerical Methods for Delay Differential Equations, Oxford University Press, Oxford, 2003.
Google Scholar
|
|
[3]
|
J. W. Brown and R. V. Churchill, Complex Variables and Applications, McGrawHill Companies, Inc. and China Machine Press, Beijing, 2004.
Google Scholar
|
|
[4]
|
H. Brunner and P. J. Van der Houwen, The numerical solution of Volterra equations. vol. 3 of CWI Monographs, North-Holland, Amsterdam, The Netherlands, 1986.
Google Scholar
|
|
[5]
|
H. Brunner, The numerical solution of neutral Volterra integro-differential equations with delay arguments, Ann. Numer. Math, 1994, 1,309-322.
Google Scholar
|
|
[6]
|
Y. Cong, Y. Wang and G. Hu, Weak delay-depentent stability of Runge-Kutta methods for differential systems with distributed delays, J. Comput. Appl. Math., 2018,342, 70-82.
Google Scholar
|
|
[7]
|
W. H. Enright and M. Hu, Continuous Runge-Kutta methods for neutral Volterra integro-differential equations with delay, Appl. Numer. Math., 1997, 24,175-190.
Google Scholar
|
|
[8]
|
J. K. Hale and S. M. Verduyn lunel, Introduction to Functional Differential Equations, Springer-Verlag, New York, 1993.
Google Scholar
|
|
[9]
|
C. Huang, Delay-dependent stability region of high order Runge-Kutta methods, Numer. Math., 2009,111,327-387.
Google Scholar
|
|
[10]
|
R. A. Horn and C. R. Johnson, Matrix Analysis, Cambridge University Press, Cambridge, 1986.
Google Scholar
|
|
[11]
|
G. Hu and T. Mitsui, Stability analysis of numerical methods for systems of neutral delay-differential equations, BIT Numer. Math., 1995, 35,504-515.
Google Scholar
|
|
[12]
|
G. Hu, Stability criteria of linear neutral systems with distributed delays, Kybernetika, 2011, 47,273-284.
Google Scholar
|
|
[13]
|
G. Hu and T. Mitsui, Delay-dependent stability of numerical methods for delay differential systems of neutral type, BIT Numer. Math., 2017, 57,731-752.
Google Scholar
|
|
[14]
|
X. Hu, Y. Cong and G. Hu, Delay-dependent stability of linear multistep methods for DAEs with multiple delays, Numer. Algor., 2018, 79,719-739.
Google Scholar
|
|
[15]
|
V. B. Kolmanavskii and A. Myshkis, Introduction to theory and Applications of Functional Differential Equations, Kluwer Academic Publishers, Dordrecht, 1999.
Google Scholar
|
|
[16]
|
T. Koto, Stability of Runge-Kutta methods for delay integro-differential equations, J. Comput. Appl. Math., 2002,145,483-492.
Google Scholar
|
|
[17]
|
J. Kuang and Y. Cong, Stability of Numerical Methods for Delay Differential Equations, Science Press, Beijing, 2005.
Google Scholar
|
|
[18]
|
J. Kuang, J. Xiang and H. Tian, The asymptotic stability of one-parameter methods for neutral differential equations, BIT Numer. Math., 1994, 34,400-408.
Google Scholar
|
|
[19]
|
J. D. Lambert, Numerical Methods for Ordinary Differential Equations, John Wiley and Sons, New York, 1991.
Google Scholar
|
|
[20]
|
S. Maset, Instability of Runge-Kutta methods when applied to linear systems of delay differential equations, Numer. Math., 2002, 90,555-562.
Google Scholar
|
|
[21]
|
Y. Xu and J. Zhao, Analysis of delay-dependent stability of linear $\theta$-methods for linear delay-integro differential equations, IMA J. Appl. Math., 2009, 74,851-869.
Google Scholar
|
|
[22]
|
C. Zhang and S. Vandewalle, Stability of Runge-Kutta methods for nonlinear Volterra delay integro-differential equations, IMA J. Numer. Anal., 2004, 24,193-214.
Google Scholar
|
|
[23]
|
C. Zhang, A class of new Pouzet-Runge-Kutta type methods for nonlinear functional integro-differential equations, Abstr. Appl. Anal., 2012, 2012, 21.
Google Scholar
|
|
[24]
|
C. Zhang and T. Qin, The mixed Runge-Kutta methods for a class of nonlinear functional-integro-differential equations, Appl. Math. Comput., 2014,237,396-404.
Google Scholar
|
|
[25]
|
J. Zhao, Y. Fan and Y. Xu, Stability of symmetric Runge-Kutta methods for neutral delay integro-differential equations, SIAM J. Numer. Anal., 2017, 55,328-348.
Google Scholar
|




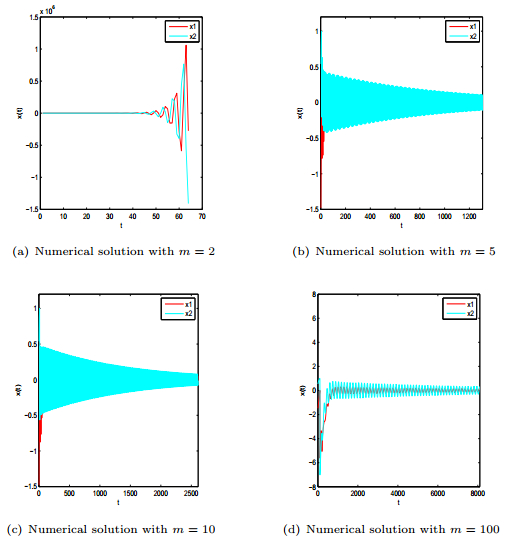

 DownLoad:
DownLoad: