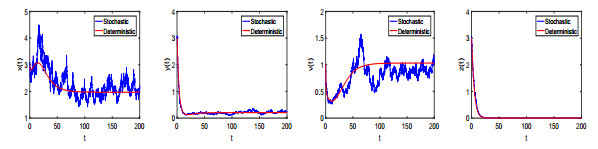
|
[1]
|
H. Chen and R. Xu, Stability and bifurcation analysis of a viral infection model with delayed immune response, Journal of Applied Analysis and Computation, 2017, 7(2), 532-553.
Google Scholar
|
|
[2]
|
N. Chitnis, J. Hyman and J. Cushing, Determining important parameters in the spread of malaria through the sensitivity analysis of a mathematical model, Bulletin of Mathematical Biology, 2008, 70(5), 1272-1296. doi: 10.1007/s11538-008-9299-0
CrossRef Google Scholar
|
|
[3]
|
N. Dalal, D. Greenhalgh and X. Mao, A stochastic model of AIDS and condom use, Journal of Mathematical Analysis and Applications, 2007, 325(1), 36-53. doi: 10.1016/j.jmaa.2006.01.055
CrossRef Google Scholar
|
|
[4]
|
A. Elaiw, A. Raezah and A. Alofi, Stability of a general delayed virus dynamics model with humoral immunity and cellular infection, Aip Advances, 2017, 7(6), 1621-1633.
Google Scholar
|
|
[5]
|
A. Etaiw and N. AlShamrani, Global stability of a delayed virus dynamics model with multi-staged infected progression and humoral immunity, Journal of Biological Systems, 2016, 9(4), 535-560.
Google Scholar
|
|
[6]
|
Y. Geng, J. Xu and J. Hou, Discretization and dynamic consistency of a delayed and diffusive viral infection model, Applied Mathematics and Computation, 2018, 316, 282-295. doi: 10.1016/j.amc.2017.08.041
CrossRef Google Scholar
|
|
[7]
|
V. Herz, S. Bonhoeffer, R. Anderson et al., Viral dynamics in vivo: Limitations on estimates of intracellular delay and virus decay, Proceedings of the National Academy of Sciences of the United States of America, 1996, 93(14), 7247-7251. doi: 10.1073/pnas.93.14.7247
CrossRef Google Scholar
|
|
[8]
|
H. Hu, F-curve, a graphical representation of protein sequences for similarity analysis based on physicochemical properties of amino acids, MATCH Communications in Mathematical and in Computer Chemistry, 2015, 73(3), 749-764.
Google Scholar
|
|
[9]
|
G. Huang, Y. Takeuchi and M. Wanbiao, Lyapunov functionals for delay differential equations model of viral infections, Siam Journal on Applied Mathematics, 2010, 70(7/8), 2693-2708.
Google Scholar
|
|
[10]
|
H. Huo, Y. Tang and L. Feng, A virus dynamics model with saturation infection and humoral immunity, International Journal of Mathematical Analysis, 2012, 6(37).
Google Scholar
|
|
[11]
|
D. Jiang, Q. Zhang, T. Hayat and A. Alsaedi, Periodic solution for a stochastic non-autonomous competitive Lotka-Volterra model in a polluted environment, Physica A Statistical Mechanics and Its Applications, 2017, 471, 276-287. doi: 10.1016/j.physa.2016.12.008
CrossRef Google Scholar
|
|
[12]
|
M. Jovanovic and M. Krstic, Analysis of non-autonomous stochastic Gompertz model with delay, Applied Mathematics and Computation, 2014, 242, 101-108. doi: 10.1016/j.amc.2014.05.046
CrossRef Google Scholar
|
|
[13]
|
D. Li and X. Cui, Dynamics of virus infection model with nonlytic immune response induced by stochastic noise, Chaos Solitons and Fractals, 2017, 99, 124-132. doi: 10.1016/j.chaos.2017.03.068
CrossRef Google Scholar
|
|
[14]
|
G. Li, Q. Yang and Y. Wei, Dynamics of stochastic heroin epidemic model with levy jumps, Journal of Applied Analysis and Computation, 2018, 8(3), 998-1010.
Google Scholar
|
|
[15]
|
J. Li, X. Song and F. Gao, Global stability of a viral infection model with two delays and two types of target cells, Journal of Applied Analysis and Computation, 2012, 2(3), 281-292.
Google Scholar
|
|
[16]
|
Y. Lin, D. Jiang and P. Xia, Long-time behavior of a stochastic SIR model, Applied Mathematics and Computation, 2014, 236, 1-9. doi: 10.1016/j.amc.2014.03.035
CrossRef Google Scholar
|
|
[17]
|
M. Liu, C. Bai and Y. Jin, Population dynamical behavior of a two-predator one-prey stochastic model with time delay, Discrete and Continuous Dynamical Systems, 2017, 37(5), 2513-2538. doi: 10.3934/dcds.2017108
CrossRef Google Scholar
|
|
[18]
|
Q. Liu, D. Jiang, N. Shi et al., Stationary distribution and extinction of a stochastic SIRS epidemic model with standard incidence, Physica A Statistical Mechanics and Its Applications, 2017, 469, 510-517. doi: 10.1016/j.physa.2016.11.077
CrossRef Google Scholar
|
|
[19]
|
S. Liu, L. Zhang and Y. Xing, Dynamics of a stochastic heroin epidemic model, Journal of Computational and Applied Mathematics, 2019, 351, 260-269. doi: 10.1016/j.cam.2018.11.005
CrossRef Google Scholar
|
|
[20]
|
S. Liu, L. Zhang, X. Zhang and A. Li, Dynamics of a stochastic heroin epidemic model with bilinear incidence and varying population size, International Journal of Biomathematics, 12(1), 1950005: 1-21.
Google Scholar
|
|
[21]
|
W. Ma, B. Ding and Q. Zhang, The existence and asymptotic behaviour of energy solutions to stochastic age-dependent population equations driven by Levy processes, Applied Mathematics and Computation, 2015, 256, 656-665. doi: 10.1016/j.amc.2015.01.077
CrossRef Google Scholar
|
|
[22]
|
X. Mao, Stochastic Differential Equations and Applications, Horwood Publishing, Chichester, 1997.
Google Scholar
|
|
[23]
|
X. Mao, G. Marion and E. Renshaw, Environmental Brownian noise suppresses explosions in population dynamics, Stochastic Processes and Their Applications, 2002, 97(1), 95-110. doi: 10.1016/S0304-4149(01)00126-0
CrossRef Google Scholar
|
|
[24]
|
A. Miao, T. Zhang, J. Zhang and W. C, Dynamics of a stochastic SIR model with both horizontal and vertical transmission, Journal of Applied Analysis and Computation, 2018, 8(4), 1108-1121.
Google Scholar
|
|
[25]
|
J. Mittler, B. Sulzer, A. Neumann and A. Perelson, Influence of delayed viral production on viral dynamics in HIV-1 infected patients, Mathematical Biosciences, 1998, 152(2), 143-163. doi: 10.1016/S0025-5564(98)10027-5
CrossRef Google Scholar
|
|
[26]
|
P. Nelson, J. Murray and A. Perelson, A model of HIV-1 pathogenesis that includes an intracellular delay, Mathematical Biosciences, 2000, 163(2), 201- 215. doi: 10.1016/S0025-5564(99)00055-3
CrossRef Google Scholar
|
|
[27]
|
M. Nowak, S. Bonhoeffer, G. Shaw and R. May, Anti-viral drug treatment: Dynamics of resistance in free virus and infected cell populations, Journal of Theoretical Biology, 1997, 184(2), 203-217. doi: 10.1006/jtbi.1996.0307
CrossRef Google Scholar
|
|
[28]
|
T. Saha and M. Bandyopadhyay, Effect of randomly fluctuating environment on autotroph-herbivore model system, International Journal of Mathematics and Mathematical Sciences, 2007, 2004(68), 3703-3716.
Google Scholar
|
|
[29]
|
Z. Teng and L. Wang, Persistence and extinction for a class of stochastic SIS epidemic models with nonlinear incidence rate, Physica A Statistical Mechanics and Its Applications, 2016, 451, 507-518. doi: 10.1016/j.physa.2016.01.084
CrossRef Google Scholar
|
|
[30]
|
X. Wang, Q. Yang and H. Huo, The asymptotic behaviors of a stochastic social epidemics model with multi-perturbation, Journal of Applied Analysis and Computation, 2018, 8(1), 272-295.
Google Scholar
|
|
[31]
|
H. Xiang, Y. Tang and H. Huo, A viral model with intracellular delay and humoral immunity, Bulletin of the Malaysian Mathematical Sciences Society, 2017, 40(3), 1011-1023. doi: 10.1007/s40840-016-0326-2
CrossRef Google Scholar
|
|
[32]
|
H. Xiang, Y. Wang and H. Huo, Analysis of the binge drinking models with demographics and nonlinear infectivity on networks, Journal of Applied Analysis and Computation, 2018, 8(5), 1535-1554.
Google Scholar
|
|
[33]
|
Q. Yang, D. Jiang, N. Shi and C. Ji, The ergodicity and extinction of stochastically perturbed SIR and SEIR epidemic models with saturated incidence, Journal of Mathematical Analysis and Applications, 2012, 388(1), 248-271. doi: 10.1016/j.jmaa.2011.11.072
CrossRef Google Scholar
|
|
[34]
|
S. Yao, Z. Ma and Z. Cheng, Pattern formation of a diffusive predatorcprey model with strong allee effect and nonconstant death rate, Physica A: Statistical Mechanics and its Applications, 2019, 527, 121350. doi: 10.1016/j.physa.2019.121350
CrossRef Google Scholar
|
|
[35]
|
L. Zhang and Y. Xing, Extremal solutions for nonlinear first-order impulsive integro-differential dynamic equations, Mathematical Notes, 2019, 105(1), 123- 131.
Google Scholar
|
|
[36]
|
X. Zhang, S. Chang, Q. Shi and H. Huo, Qualitative study of a stochastic sisepidemic model with vertical transmission, Physica A Statistical Mechanics and Its Applications, 2018, 505, 805-817. doi: 10.1016/j.physa.2018.04.022
CrossRef Google Scholar
|
|
[37]
|
X. Zhang, H. Huo, H. Xiang and D. Li, The dynamic behavior of deterministic and stochastic delayed SIQS model, Journal of Applied Analysis and Computation, 2018, 8(4), 1061-1084.
Google Scholar
|
|
[38]
|
X. Zhang, S. Ma, H. Huo and D. Li, Dynamic behavior of a stochastic SIQS epidemic model with Levy jumps, Nonlinear Dynamics, 2018, 1, 1-13.
Google Scholar
|
|
[39]
|
Y. Zhao, S. Yuan and Q. Zhang, The effect of Levy noise on the survival of a stochastic competitive model in an impulsive polluted environment, Applied Mathematical Modelling, 2016, 40(17-18), 7583-7600. doi: 10.1016/j.apm.2016.01.056
CrossRef Google Scholar
|
|
[40]
|
J. Zhou and Y. Yang, Global dynamics of a discrete viral infection model with time delay, virus-to-cell and cell-to-cell transmissions, Journal of Difference Equations and Applications, 2017, 23(11), 1853-1868. doi: 10.1080/10236198.2017.1371144
CrossRef Google Scholar
|




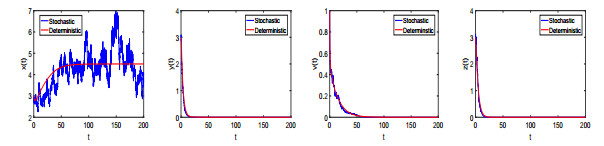

 DownLoad:
DownLoad: