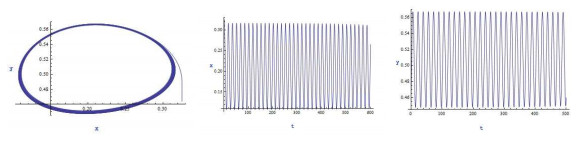
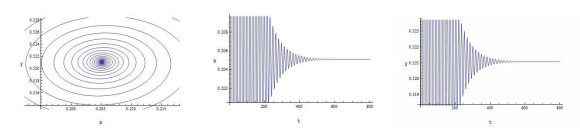
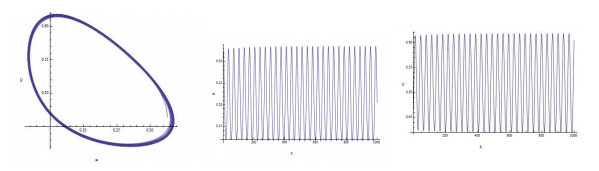
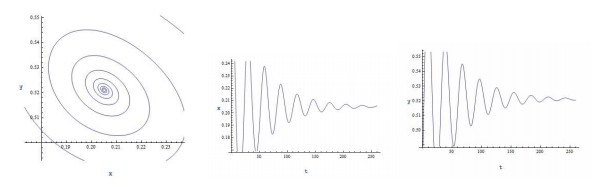
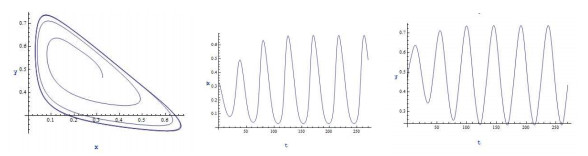
|
[1]
|
E. Beretta and Y. Kuang, Global analyses in some delayed ratio-dependent predator-prey systems, Nonlinear Anal.: Theory Methods Appl., 1998, 32(3), 381-408. doi: 10.1016/S0362-546X(97)00491-4
CrossRef Google Scholar
|
|
[2]
|
P. H. Crowley and E. K. Martin, Functional responses and interference within and between year classes of a dragonfly population, J N Am Benth Soc, 1989, 8(3), 211-221. doi: 10.2307/1467324
CrossRef Google Scholar
|
|
[3]
|
Q. Dong, W. Ma and M. Sun, The asymptotic behaviour of a chemostat model with Crowley-Martin type functional response and time delays, J Math Chem, 2013, 51(5), 1231-1248. doi: 10.1007/s10910-012-0138-z
CrossRef Google Scholar
|
|
[4]
|
B. D. Hassard, N. D. Kazarinoff and Y. H. Wan, Theory and Applications of Hopf Bifurcation, Cambridge University Press, Cambridge, UK, 1982, 62, 713-714.
Google Scholar
|
|
[5]
|
A. Lotka, Elements of mathematical biology, NewYork: Dover Publications, 1958, 47, 764.
Google Scholar
|
|
[6]
|
S. M. Li and X. F. Tan, Stability analysis of an enterprise competitive model with time delay, JAAC, 2016, 3, 684-689.
Google Scholar
|
|
[7]
|
S. Ruan and J. Wei, On the zero of some transcendential functions with applications to stability of delay differential equations with two delays, Dyn. Contin. DiscreteImpuls. Syst. Ser. A, 2003, 10, 863-874.
Google Scholar
|
|
[8]
|
G. T. Sklaski and J. F. Gilliam, Functional responses with predator interference: viable alter native to Holling typeII model, Ecology, 2001, 82(11), 3083-3092. doi: 10.1890/0012-9658(2001)082[3083:FRWPIV]2.0.CO;2
CrossRef Google Scholar
|
|
[9]
|
Y. Song and J. Wei, Bifurcation analysis for Chen's system with delayed feedback and its application to Control of chaos, Chaos, Solitons & Fractals, 2004, 22(1), 75-91.
Google Scholar
|
|
[10]
|
J. P. Tripathia, S. Tyagia and S. Abbasa, Global analysis of a delayed density dependent predator-prey model with Crowley-Martin functional response, Commun. Nonlinear Sci. Numer. Simul, 2016, 30, 45-69. doi: 10.1016/j.cnsns.2015.06.008
CrossRef Google Scholar
|
|
[11]
|
X. Tian and R. Xu, Stability analysis of an SEIS epidemic model with nonlinear incidence and time delay, JAAC, 2014, 4, 405-418.
Google Scholar
|
|
[12]
|
R. K. Upadhyay and R. K. Naji, Dynamics of three species food chain model with Crowley-Martin type functional response, Chaos, Solitons & Fractals, 2009, 42(3), 1337-1346.
Google Scholar
|
|
[13]
|
R. K. Upadhyay, S. N. Raw and V. Rai, Dynamic complexities in a tri-trophic food chain model with Holling type Ⅱ and Crowley-Martin functional response, Nonlinear Anal.: Model Control, 2010, 15(3), 361-375.
Google Scholar
|
|
[14]
|
X. Wu and C. Zhang, Dynamic properties of the Oregonator model with delay, JAAC, 2012, 2(1), 91-102.
Google Scholar
|




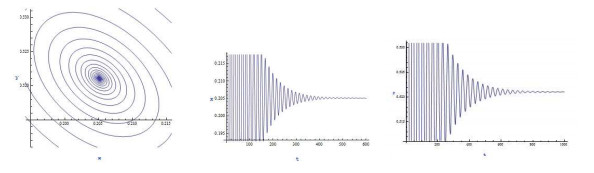

 DownLoad:
DownLoad: