| Citation: | Yongshun Zhao, Shurong Sun. EIGENVALUE PROBLEM FOR FRACTIONAL DIFFERENCE EQUATION WITH NONLOCAL CONDITIONS[J]. Journal of Applied Analysis & Computation, 2021, 11(1): 32-44. doi: 10.11948/20180305 |
EIGENVALUE PROBLEM FOR FRACTIONAL DIFFERENCE EQUATION WITH NONLOCAL CONDITIONS
-
Abstract
In this work, we investigate a class of boundary value problem for fractional difference equation with nonlocal conditions
$ \begin{cases}\Delta^{\nu}u(t)+\lambda f(t+\nu-1, u(t+\nu-1)) = 0, t\in\mathbb{N}_{0}^{b+1},\\ u(\nu-2) = h(u), \Delta u(\nu+b) = g(u), \end{cases} $
where $ 1<\nu\leq2 $ is a real number, $ f:\mathbb{N}_{\nu-1}^{\nu+b}\times\mathbb{R}\rightarrow(0, +\infty) $ is a continuous function, $ g, h $ are given functionals, $ b\geq2 $ is an integer, $ \lambda>0 $ is a parameter. By upper and lower solutions method, we can present the existence result of positive solutions. The eigenvalue intervals to this problem are studied by the properties of the Green function and Guo-Krasnosel'skii fixed point theorem in cones.
-

-
References
[1] T. Abdeljawad, On riemann and caputo fractional differences, Applied Mathematics and Computation, 2011, 62(3), 1602-1611. [2] I. Area, J. Losada and J. Nieto, On quasi-periodic properties of fractional sums and fractional differences of periodic functions, Applied Mathematics and Computation, 2016, 273(6), 190-200. [3] F. Atici and P. Eloe, Two-point boundary value problems for finite fractional difference equations, Journal of Difference Equations and Applications, 2011, 17(4), 445-456. doi: 10.1080/10236190903029241 [4] Z. Bai and H. Lu, Positive solutions for boundary value problem of nonlinear fractional differential equation, Journal of Mathematical Analysis and Applications, 2005, 311(2), 495-505. doi: 10.1016/j.jmaa.2005.02.052 [5] Y. Chen and X. Tang, The difference between a class of discrete fractional and integer order boundary value problems, Applied Mathematics and Computation, 2014, 19(12), 4025-4067. [6] Y. Cui, W. Ma, Q. Sun and X. Su, New uniqueness results for boundary value problem of fractional differential equation, Nonlinear Analysis: Modelling and Control, 2018, 23(1), 31-39. [7] C. Goodrich, Solutions to a discrete right-focal fractional boundary value problem, International Journal of Difference Equations, 2010, 5, 195-216. [8] C. Goodrich, Existence and uniqueness of solutions to a fractional difference equation with nonlocal conditions, Computers and Mathematics with Applications, 2011, 61, 191-201. doi: 10.1016/j.camwa.2010.10.041 [9] C. Goodrich and A. Peterson, Discrete fractional calculus, Springer International Publishing, Switzerland, 2015. [10] J. Graef, L. Kong and B. Yang, Positive solutions for a fractional boundary value problem, Applied Mathematics Letters, 2016, 56, 49-55. doi: 10.1016/j.aml.2015.12.006 [11] X. Li, T. Caraballo, R. Rakkiyappan and X. Han, On the stability of impulsive functional differential equations with infinite delays, Mathematical Methods in the Applied Sciences, 2015, 38(14), 3130-3140. doi: 10.1002/mma.3303 [12] X. Li, J. Shen and R. Rakkiyappan, Persistent impulsive effects on stability of functional differential equations with finite or infinite delay, Applied Mathematics and Computation, 2018, 329, 14-22. doi: 10.1016/j.amc.2018.01.036 [13] X. Liu and M. Jia, Multiple solutions for fractional differential euqations with nonlinear boundary conditions, Computers & Mathematics with Applications, 2010, 59(8), 2880-2886. [14] Y. Pan, Z. Han and D. Yang, The existence and nonexistence of positive solutions to a discrete fractional boundary value problem with a parameter, Applied Mathematics Letters, 2014, 36, 1-6. doi: 10.1016/j.aml.2014.04.015 [15] V. Tarasov, Discrete model of dislocations in fractional nonlocal elasticity, Journal of King Saud University-Science, 2016, 28, 33-36. doi: 10.1016/j.jksus.2015.04.001 [16] G. Wu, T. Abdeljawad, J. Liu et al., Mittag-leffler stability analysis of fractional discrete-time neural networks via fixed point technique, Nonlinear Analysis: Modelling and Control, 2019, 24(6), 919-936. [17] G. Wu and D. Baleanu, Discrete fractional logistic map and its chaos, Nonlinear Dynamics, 2014, 75, 283-287. doi: 10.1007/s11071-013-1065-7 [18] G. Wu, D. Baleanu and W. Luo, Mittag-leffler function for discrete fractional modelling, Journal of King Saud University-Science, 2016, 28, 99-102. doi: 10.1016/j.jksus.2015.06.004 [19] M. Xu and Z. Han, Positive solutions for integral boundary value problem of two-term fractional differential equations, Boundary Value Problems, 2018, 100, 1-13. [20] X. Zhang and Q. Zhong, Uniquencess of solution for higher-order fractional differential equations with conjugate type integral conditions, Fractional Calculus and Applied Analysis, 2017, 20(6), 1471-1484. [21] X. Zhang and Q. Zhong, Triple positive solutions for nonlocal fractional differential equations with singularities both on time and space variables, Applied Mathematics Letters, 2018, 80, 12-19. doi: 10.1016/j.aml.2017.12.022 [22] Y. Zhao, S. Sun, Z. Han and M. Zhang, Positive solutions for boundary value problems of nonlinear fractional differential equations, Applied Mathematics and Computation, 2011, 217(16), 6950-6958. doi: 10.1016/j.amc.2011.01.103 -
-
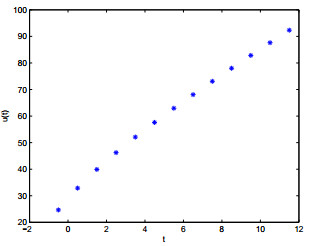
- Figure 1. The solution of problem (5.1) with λ = 0.45.




 DownLoad:
DownLoad: