| Citation: |
Jian-Guo Liu, Wen-Hui Zhu, Li Zhou. INTERACTION SOLUTIONS AND ABUNDANT EXACT SOLUTIONS FOR THE NEW (3+1)-DIMENSIONAL GENERALIZED KADOMTSEV-PETVIASHVILI EQUATION IN FLUID MECHANICS[J]. Journal of Applied Analysis & Computation, 2020, 10(3): 960-971. doi: 10.11948/20190172
|
INTERACTION SOLUTIONS AND ABUNDANT EXACT SOLUTIONS FOR THE NEW (3+1)-DIMENSIONAL GENERALIZED KADOMTSEV-PETVIASHVILI EQUATION IN FLUID MECHANICS
-
Abstract
In this work, we present the interaction solutions and abundant exact solutions for the new (3+1)-dimensional generalized Kadomtsev-Petviashvili equation based on the Hirota's bilinear form and a direct function. The obtained interaction solutions contain the interaction between the rational function and the $\tanh$ function and the interaction between the rational function and the $\cos$ function. The dynamical properties of these resulting solutions are analyzed and shown in three-dimensional plots, corresponding contour graphs and plane figures.-
Keywords:
- Interaction solutions /
- bilinear form /
- exact solutions /
- dynamical properties
-
-
References
[1] F. Baronio, A. Degasperis, M. Conforti et al., Solutions of the vector nonlinear Schröinger equations: evidence for deterministic rogue waves, Phys. Rev. Lett., 2012, 109, 044102. doi: 10.1103/PhysRevLett.109.044102 [2] S. Chen and W. Ma, Lump solutions to a generalized Bogoyavlensky-Konopelchenko equation, Front. Math. China., 2018, 13(3), 525-534. doi: 10.1007/s11464-018-0694-z [3] C. Dai, Y. Wang and J. Zhang, Analytical spatiotemporal localizations for the generalized $(3+1)$-dimensional nonlinear Schrödinger equation, Opt. Lett., 2010, 35, 1437-1439. doi: 10.1364/OL.35.001437 CrossRef $(3+1)$-dimensional nonlinear Schrödinger equation" target="_blank">Google Scholar
[4] C. Dai, X. Zhang, Y. Fan et al., Localized modes of the $(n+1)$-dimensional schrödinger equation with power-law nonlinearities in PT-symmetric potentials, Commun. Nonlinear. Sci., 2017, 43, 239-250. doi: 10.1016/j.cnsns.2016.07.002 CrossRef $(n+1)$-dimensional schrödinger equation with power-law nonlinearities in PT-symmetric potentials" target="_blank">Google Scholar
[5] B. Ghanbari, A. Bekir and R. K. Saeed, Oblique optical solutions of mitigating internet bottleneck with quadratic-cubic nonlinearity, Int. J. Mod. Phys. B., 2019, 33(20), 1950224. [6] B. Ghanbari and N. Raza, An analytical method for soliton solutions of perturbed Schrödinger's equation with quadratic-cubic nonlinearity, Mod. Phys. Lett. B., 2019, 33(3), 1950018. [7] B. Ghanbari, M. Inc and L. Rada, Solitary wave solutions to the tzitzeica type equations obtained by a new efficient approach, J. Appl. Anal. Comput., 2019, 9(2), 568-589. [8] J. Gao, L. Han and Y. Huang, Solitary Waves for the Generalized Nonautonomous Dual-power Nonlinear Schrödinger Equations with Variable Coefficients, Journal of Nonlinear Modeling and Analysis, 2019, 1, 251-260. [9] B. Ghanbari and M. Inc, A new generalized exponential rational function method to find exact special solutions for the resonance nonlinear Schrödinger equation, Eur. Phys. J. Plus., 2018, 133, 142. doi: 10.1140/epjp/i2018-11984-1 [10] B. Ghanbari, M. S. Osman and D. Baleanu, Generalized exponential rational function method for extended Zakharov-Kuzetsov equation with conformable derivative, Mod. Phys. Lett. A., 2019, 34(20), 1950155. doi: 10.1142/S0217732319501554 [11] B. Ghanbari and J. F. Gómez-Aguilar, New exact optical soliton solutions for nonlinear Schrödinger equation with second-order spatio-temporal dispersion involving M-derivative, Mod. Phys. Lett. B., 2019, 33(20), 1950235. doi: 10.1142/S021798491950235X [12] B. Ghanbari, Abundant soliton solutions for the Hirota-Maccari equation via the generalized exponential rational function method, Mod. Phys. Lett. B., 2019, 33(9), 1950106. doi: 10.1142/S0217984919501069 [13] B. Ghanbari and C. Kuo, New exact wave solutions of the variable-coefficient $(1+1)$-dimensional Benjamin-Bona-Mahony and $(2+1)$-dimensional asymmetric Nizhnik-Novikov-Veselov equations via the generalized exponential rational function method, Eur. Phys. J. Plus., 2019, 134, 334. [14] B. Ghanbari, A. Yusuf, M. Inc et al., The new exact solitary wave solutions and stability analysis for the $(2+1)$-dimensional zakharov-kuznetsov equation, Adv. Differ. Equ., 2019, 49, 1-15. $(2+1)$-dimensional zakharov-kuznetsov equation" target="_blank">Google Scholar
[15] B. Ghanbari, M. Inc, A. Yusuf et al., Exact optical solitons of Radhakrishnan-Kundu-Lakshmanan equation with Kerr law nonlinearity, Mod. Phys. Lett. B., 2019, 33(6), 1950061. doi: 10.1142/S0217984919500611 [16] L. Huang and Y. Chen, Lump solutions and interaction phenomenon for $(2+1)$-dimensional sawada-kotera equation, Commun. Theor. Phys., 2017, 67(5), 473-478. doi: 10.1088/0253-6102/67/5/473 CrossRef $(2+1)$-dimensional sawada-kotera equation" target="_blank">Google Scholar
[17] Y. Kong, L. Xin, Q. Qiu et al., Exact periodic wave solutions for the modified Zakharov equations with a quantum correction, Appl. Math. Lett., 2019, 94, 140-148. doi: 10.1016/j.aml.2019.01.009 [18] C. Kuo and B. Ghanbari, Resonant multi-soliton solutions to new $(3+1)$-dimensional Jimbo-Miwa equations by applying the linear superposition principle, Nonlinear Dyn., 2019, 96(1), 459-464. [19] J. Liu and Y. He, New periodic solitary wave solutions for the $(3+1)$-dimensional generalized shallow water equation, Nonlinear Dyn., 2017, 90(1), 363-369. $(3+1)$-dimensional generalized shallow water equation" target="_blank">Google Scholar
[20] J. Liu, Y. Tian and Z. Zeng, New exact periodic solitary-wave solutions for the new $(3+1)$-dimensional generalized Kadomtsev-Petviashvili equation in multi-temperature electron plasmas, AIP. Adv., 2017, 7, 105013. doi: 10.1063/1.4999913 CrossRef $(3+1)$-dimensional generalized Kadomtsev-Petviashvili equation in multi-temperature electron plasmas" target="_blank">Google Scholar
[21] J. Li and Y. Zhou, Exact Solutions in Invariant Manifolds of Some Higher-Order Models Describing Nonlinear Waves, Qual. Theor. Dyn. Syst., 2019, 18(1), 183-199. [22] J. Li, G. Chen and S. Deng, Smooth Exact Traveling Wave Solutions Determined by Singular Nonlinear Traveling Wave Systems: Two Models, Int. Bifurcat. Chaos., 2019, 29(4), 1950047. doi: 10.1142/S0218127419500470 [23] J. Li and G. Chen, More on Bifurcations and Dynamics of Traveling Wave Solutions for a Higher-Order Shallow Water Wave Equation, Internat. J. Bifur. Chaos Appl. Sci. Engrg., 2019, 29(1), 1950014. [24] Z. Lan, Periodic, breather and rogue wave solutions for a generalized $(3+1)$-dimensional variable-coefficient B-type Kadomtsev-Petviashvili equation in fluid dynamics, Appl. Math. Lett., 2019, 94, 126-132. [25] Z. Lan, W. Hu and B. Guo, General propagation lattice Boltzmann model for a variable-coefficient compound KdV-Burgers equation, Appl. Math. Model., 2019, 73, 695-714. doi: 10.1016/j.apm.2019.04.013 [26] Z. Lan, Dark solitonic interactions for the $(3+1)$-dimensional coupled nonlinear Schrödinger equationsin nonlinear optical fibers, Opt. Laser Technol., 2019, 113, 462-466. doi: 10.1016/j.optlastec.2018.12.040 CrossRef $(3+1)$-dimensional coupled nonlinear Schrödinger equationsin nonlinear optical fibers" target="_blank">Google Scholar
[27] Z. Lan and J. Su, Solitary and rogue waves with controllable backgrounds for the non-autonomous generalized AB system, Nonlinear Dyn., 2019, 96, 2535-2546. doi: 10.1007/s11071-019-04939-1 [28] Z. Lan and B. Gao, Lax pair, infinitely many conservation laws and solitons for a (2 + 1)-dimensional Heisenberg ferromagnetic spin chain equation with time-dependent coefficients, Appl. Math. Lett., 2018, 79, 6-12. doi: 10.1016/j.aml.2017.11.010 [29] Z. Lan, Rogue wave solutions for a coupled nonlinear Schrödinger equation in the birefringent optical fiber, Appl. Math. Lett., 2019, 98, 128-134. doi: 10.1016/j.aml.2019.05.028 [30] Z. Lan, Multi-soliton solutions for a $(2+1)$-dimensional variable-coefficient nonlinear Schrödinger equation, Appl. Math. Lett., 2018, 86, 243-248. [31] Y. Li and J. Liu, Multiple periodic-soliton solutions of the $(3 + 1)$-dimensional generalised shallow water equation, Pramana., 2018, 90, 71. doi: 10.1007/s12043-018-1568-3 CrossRef $(3 + 1)$-dimensional generalised shallow water equation" target="_blank">Google Scholar
[32] Y. Li and J. Liu, New periodic solitary wave solutions for the new $(2+1)$-dimensional Korteweg-de Vries equation, Nonlinear Dyn., 2018, 91(1), 497-504. $(2+1)$-dimensional Korteweg-de Vries equation" target="_blank">Google Scholar
[33] W. Ma and Y. Zhou, Lump solutions to nonlinear partial differential equations via Hirota bilinear forms, J. Differ. Equations., 2018, 264, 2633-2659. doi: 10.1016/j.jde.2017.10.033 [34] W. Ma, Riemann-Hilbert problems and N-soliton solutions for a coupled mKdV system, J. Geom. Phys., 2018, 132, 45-54. [35] W. Ma and A. Abdeljabbar, A bilinear bäcklund transformation of a $(3+1)$-dimensional generalized KP equation, Appl. Math. Lett, 2012, 25(10), 1500-1504. doi: 10.1016/j.aml.2012.01.003 CrossRef $(3+1)$-dimensional generalized KP equation" target="_blank">Google Scholar
[36] M. S. Osman, B. Ghanbari and J. A. T. Machado, New complex waves in nonlinear optics based on the complex Ginzburg-Landau equation with Kerr law nonlinearity, Eur. Phys. J. Plus., 2019, 134, 20. doi: 10.1140/epjp/i2019-12442-4 [37] H. M. Srivastava, H. Günerhan and B. Ghanbari, Exact traveling wave solutions for resonance nonlinear Schrödinger equation with intermodal dispersions and the Kerr law nonlinearity, Math. Method. Appl. Sci., 2019, https://doi.org/10.1002/mma.5827. [38] A. M. Wazwaz and S. A. El-Tantawy, A new $(3+1)$-dimensional generalized kadomtsev-petviashvili equation, Nonlinear Dyn., 2016, 84(2), 1107-1112. doi: 10.1007/s11071-015-2555-6 CrossRef $(3+1)$-dimensional generalized kadomtsev-petviashvili equation" target="_blank">Google Scholar
[39] G. Xu and A. M. Wazwaz, Characteristics of integrability, bidirectional solitons and localized solutions for a $(3 + 1)$-dimensional generalized breaking soliton equation, Nonlinear Dyn., 2019, 96, 1989-2000. doi: 10.1007/s11071-019-04899-6 CrossRef $(3 + 1)$-dimensional generalized breaking soliton equation" target="_blank">Google Scholar
-
-
Figures(8)
Export File
Citation
Jian-Guo Liu, Wen-Hui Zhu, Li Zhou. INTERACTION SOLUTIONS AND ABUNDANT EXACT SOLUTIONS FOR THE NEW (3+1)-DIMENSIONAL GENERALIZED KADOMTSEV-PETVIASHVILI EQUATION IN FLUID MECHANICS[J]. Journal of Applied Analysis & Computation, 2020, 10(3): 960-971. doi: 10.11948/20190172
Format
Content
DownLoad:
-
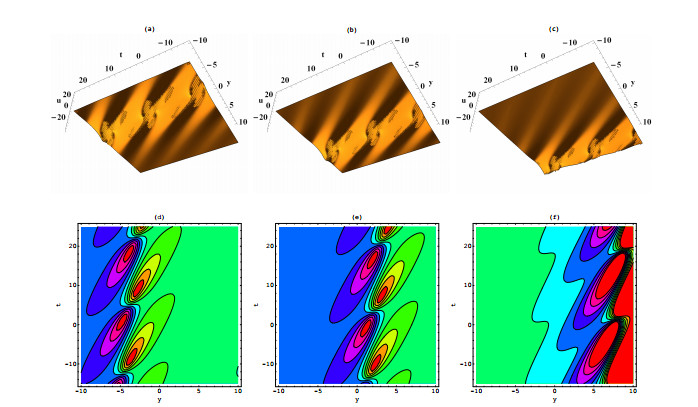
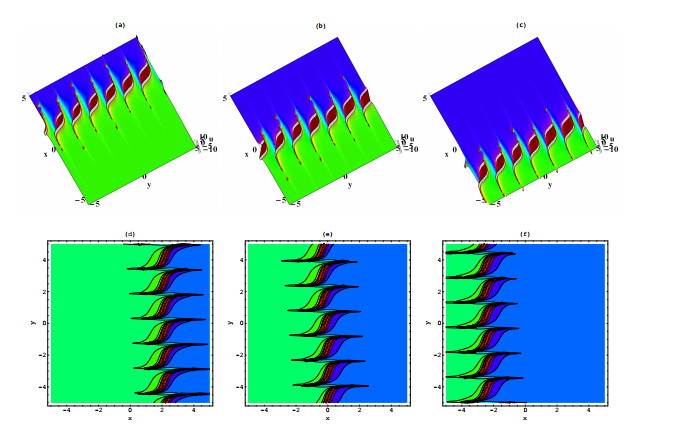
Figure 1. Plots of the interaction solutions (2.6) for
$ \iota_1 = \iota_6 = 2 $ ,$ k = t = 1 $ ,$ \iota_3 = -1 $ ,$ \iota_5 = 5 $ ,$ \iota_{11} = -6 $ ,$ \iota_{10} = 3 $ ,$ j_3 = -2 $ , when$ x = -5 $ in (a) (d) (g),$ x = 0 $ in (b) (e) (h) and$ x = 5 $ in (c) (f) (i).$ y = -8 $ in (g) (h) and (i). -
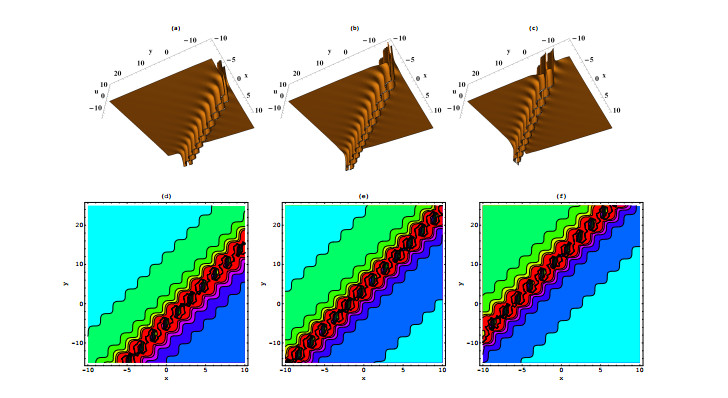
Figure 2. Plots of the interaction solutions (3.3) for
$ \iota_1 = \iota_5 = j_1 = 2 $ ,$ \iota_2 = -1 $ ,$ z = \iota_6 = 0 $ ,$ \iota_{11} = -6 $ ,$ \iota_{10} = 3 $ ,$ j_3 = -2 $ , when$ x = -3 $ in (a) (d),$ x = 0 $ in (b) (e) and$ x = 3 $ in (c) (f). -
Figure 3. Plots of the interaction solutions (3.3) for
$ \iota_1 = \iota_5 = j_1 = 2 $ ,$ \iota_2 = -1 $ ,$ \iota_6 = 1 $ ,$ t = 20 $ $ \iota_{11} = -6 $ ,$ \iota_{10} = 3 $ ,$ j_3 = -2 $ , when$ z = -35 $ in (a) (d),$ z = 0 $ in (b) (e) and$ z = 35 $ in (c) (f). -
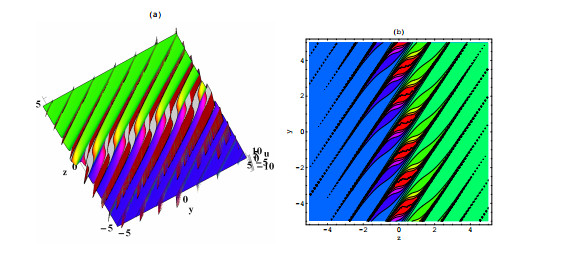
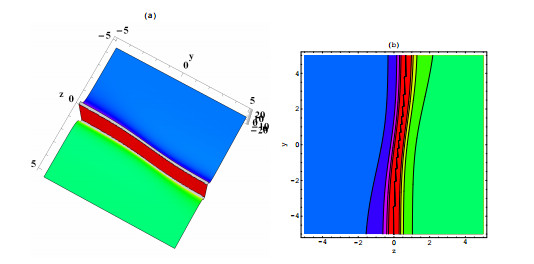
Figure 4. Solution (4.3) with
$ \Lambda _1 = -2 $ ,$ \Lambda _2 = 1 $ ,$ \Lambda _3 = 0 $ ,$ x = t = 0 $ , (a) three-dimensional graph (b) contour graph. -
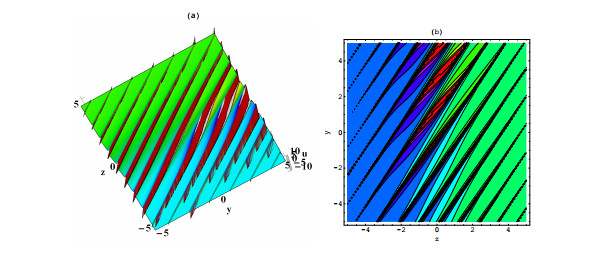
Figure 5. Solution (4.3) with
$ \Lambda _1=0 $ ,$ \Lambda _2=1 $ ,$ \Lambda _3=1 $ ,$ x=t=0 $ , (a) three-dimensional graph (b) contour graph. -
Figure 6. Solution (4.3) with
$ \Lambda _1=-2 $ ,$ \Lambda _2=0 $ ,$ \Lambda _3=1 $ ,$ x=t=0 $ , (a) three-dimensional graph (b) contour graph. -
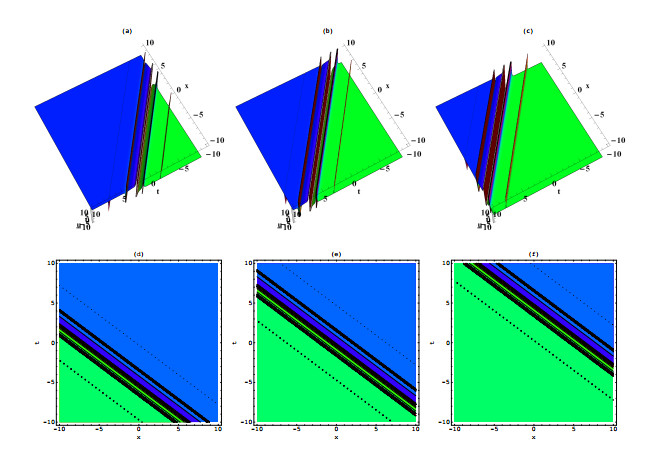
Figure 7. Solution (4.3) with
$ \Lambda _1 = -2 $ ,$ \Lambda _2 = 1 $ ,$ \Lambda _3 = 1 $ ,$ z = 0 $ , when$ t = -5 $ in (a) (d),$ t = 0 $ in (b) (e) and$ t = 5 $ in (c) (f). -
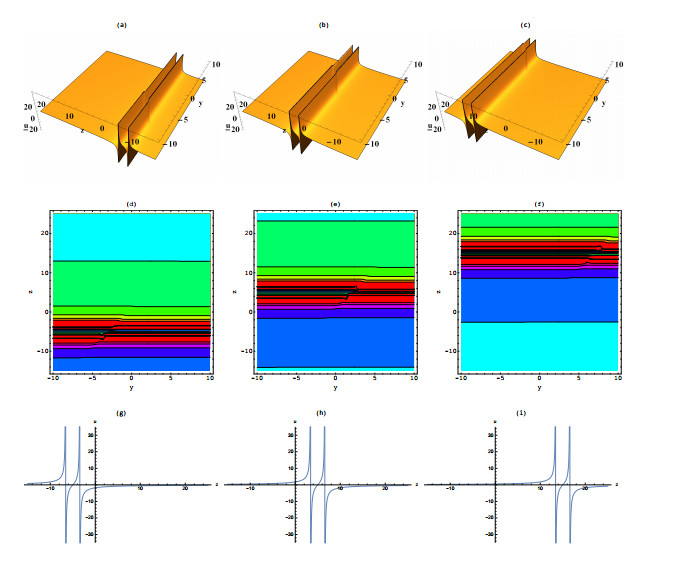
Figure 8. Solution (4.9) when
$ z = -10 $ in (a) (d),$ z = 0 $ in (b) (e) and$ z = 10 $ in (c) (f).