| Citation: | Junliang Lu, Xiaochun Hong, Qi Zhao. NEW EXACT SOLUTIONS FOR COUPLED SCHRÖDINGER-BOUSSINESQ EQUATIONS[J]. Journal of Applied Analysis & Computation, 2021, 11(2): 741-765. doi: 10.11948/20190380 |
NEW EXACT SOLUTIONS FOR COUPLED SCHRÖDINGER-BOUSSINESQ EQUATIONS
-
Abstract
Due to the importance of the coupled Schrödinger-Boussinesq equations (CSBEs) in applied physics, many mathematicians and physicists are interesting to CSBEs. One of the main tasks of studying CSBEs is to obtain the exact solutions for CSBEs. In this paper, we firstly use the coupled Riccati equations to change the polynomial expansion method. Secondly, CSBEs are changed into coupled ordinary differential equations by the traveling wave solution transformation. Then, we assume that the solutions for the coupled ordinary differential equations satisfy the coupled Riccati equations and substitute the solutions of the coupled Riccati equations into the coupled ordinary differential equations. By calculating the algebra system, we successfully construct more new exact traveling wave solutions for CSBEs with distinct physical structures. The exact solutions with arbitrary parameters are expressed by sech, sech2, tanh, sinh, cosh, et al, functions, respectively. When the parameters are taken as special values, some examples are given to demonstrate the solutions and their physical meaning.
-

-
References
[1] H. I. Abdel-Gawad and M. Osman, Exact solutions of the korteweg-de vries equation with space and time dependent coefficients by the extended unified method, Indian J Pure Appl Math., 2014, 45, 1-12. DOI: 10.1007/s13226-014-0047-x. [2] N. Alam Khan, N. Alam Khan, S. Ullah and et al, Swirling flow of couple stress fluid due to a rotating disk, Nonlinear Engineering, 2019, 8, 261-269. Https://doi.org/10.1515/nleng-2017-0062. doi: 10.1515/nleng-2017-0062 [3] K. Ali, M. Osman and M. Abdel-Aty, New optical solitary wave solutions of fokas-lenells equation in optical fiber via sine-gordon expansion method, Alexandria Eng. J., 2020. Https://doi.org/10.1016/j.aej.2020.01.037. doi: 10.1016/j.aej.2020.01.037 [4] K. K. Ali, A. M. Wazwaz and M. Osman, Optical soliton solutions to the generalized nonautonomous nonlinear schrödinger equations in optical fibers via the sine-gordon expansion method, Optik, 2020, 208, 164132. Https://doi.org/10.1016/j.ijleo.2019.164132. doi: 10.1016/j.ijleo.2019.164132 [5] A. Bazine, D. Jemmeli, M. Belhaj and C. Dridi, New modeling method for uv sensor photoelectrical parameters extraction, OptikInternational Journal for Light and Electron Optics, 2019, 181, 906-913. Https://doi.org/10.1016/j.ijleo.2018.12.171. doi: 10.1016/j.ijleo.2018.12.171 [6] Y. Bogomolov, I. Kolchugina, A. Litvak and et al, Near-sonic langmuir solitons, Lett. A, 1982, 91, 447-450. DOI: 10.1016/0375-9601(82)90746-0. [7] J. Cai, B. Yang and C. Zhang, Efficient mass-and energy-preserving schemes for the coupled nonlinear schrödinger-boussinesq system, Applied Mathematics Letters, 2019, 91, 76-82. DOI: org/10.1016/j.aml.2018.11.024. [8] Y. Ding, M. Osman and A. M. Wazwaz, Abundant complex wave solutions for the nonautonomous fokas-lenells equation in presence of perturbation terms, Optik-International Journal for Light and Electron Optics, 2019, 181, 503-513. Https://doi.org/10.1016/j.ijleo.2018.12.064. doi: 10.1016/j.ijleo.2018.12.064 [9] E. Fan, Extended tanh-function method and its applications to nonlinear equations, Phys. Lett. A, 2000, 277, 212-218. DOI:org/10.1016/S0375- 9601(00)00725-8. [10] D. Feng, J. Lu, J. Li and T. He, Bifurcation studies on traveling wave solutions for nonlinear intensity klein-gordon equation, Applied Mathematics and Computation, 2007, 189(1), 271-284. DOI: org/10.1016/j.amc.2006.11.106. [11] D. Feng, J. Lu, J. Li and T. He, New explicit and ecact solutions for a system fo variant rlw equations, Applied Mathematics and Computation, 2008, 198(2), 715-720. Https://doi.org/10.1016/j.amc.2007.09.009. doi: 10.1016/j.amc.2007.09.009 [12] J. Gao, L. Han and Y. Huang, Solitary waves for the generalized nonautonomous dual-power nonlinear schrodinger equations with variable coefficients, Journal of Nonlinear Modeling and Analysis, 2019, 1(2), 251-260. DOI:10.12150/jnma.2019.251. [13] B. Ghanbari, M. S. Osman and D. Baleanu, New optical solitary wave solutions of fokas-lenells equation in presence of perturbation terms by a novel approach, Optik-International Journal for Light and Electron Optics, 2018, 175, 328-333. Https://doi.org/10.1016/j.ijleo.2018.08.007. doi: 10.1016/j.ijleo.2018.08.007 [14] B. Ghanbari, M. S. Osman and D. Baleanu, Generalized exponential rational function method for extended zakharov kuzetsov equation with conformable derivative, Modern Physics Letters A, 2019, 34(20), 1950155(16 pages). Https://doi.org/10.1142/S0217732319501554. [15] B. Guo and F. Chen, Finite dimensional behavior of global attractors for weakly damped nonlinear schrödinger-boussinesq equations, Physica D, 1996, 93, 101- 118. DOI: org/10.1016/0167-2789(95)00277-4. [16] B. Guo and X. Du, Existence of the periodic solution for the weakly damped schrödinger-boussinesq equation, Journal of Mathematical Analysis and Applications, 2001, 262, 453-472. DOI:10.1006/jmaa.2000.7455. [17] B. Guo and X. Du, Existence of the periodic solution for the weakly damped schrödinger-boussinesq equation, Journal of Mathematical Analysis and Applications, 2001, 262(2), 453-472. DOI:10.1006/jmaa.2000.7455. [18] Y. Gurefe, A. Sonmezoglu and E. Misirli, Application of the trial equation method for solving some nonlinear evolution equations arising in mathematical physics, RAMANA-journal of physics, 2011, 77(6), 1023-1029. DOI:org/10.1007/s12043-011-0201-5. [19] R. Hirota and J. Satsuma, Soliton solution of a coupled kdv equation, Phys. Lett. A, 1981, 85, 407-408. DOI:org/10.1016/0375-9601(81)90423-0. [20] X. Hu, B. Guo and H. Tam, Homoclinic orbits for the coupled schrödingeboussinesq equation and coupled higgs equation, Journal of the Physical Society of Japan, 2003, 72(1), 189-190. DOI: org/10.1143/JPSJ.72.189. [21] L. Huang, Y. Jiao and D. Liang, Multi-symplectic scheme for the coupled schrödinger-boussinesq equations, 2013, 22(7), 070201. [22] B. Inan, A. T. OsmanMS and D. Baleanu, Analytical and numer ical solutions of mathematical biology models: The newell-whitehead segel and allen-cahn equations, Math. Meth. Appl. Sci., 2019, 1-13. Https://doi.org/10.1002/mma.6067. doi: 10.1002/mma.6067 [23] A. Javid, N. Raza and M. S. Osman, Multi-solitons of thermophoretic mo tion equation depicting the wrinkle propagation in substrate-supported graphene sheets, Commun. Theor. Phys., 2019, 71(4), 362-366. DOI: 10.1088/0253- 6102/71/4/362. [24] J. Li and G. Chen, Bifurcations of traveling wave and breather solutions of a general class of nonlinear wave equations, Int. J. Bifurcation and Chaos, 2005, 15(9), 2913-2926. DOI: 10.1142/S0218127405013770. [25] Y. Li and Q. Chen, Finite dimensional global attractor for dissipative schrödinger-boussinesq equations, Journal of mathematical analysis and ap plications, 1997, 205, 107-132. DOI:org/10.1006/jmaa.1996.5148. [26] F. Liao, L. Zhang and S. Wang, Numerical analysis of cubic orthog onal spline collocation methods for the coupled schrödinger-boussinesq equations, Applied Numerical Mathematics, 2017, 119, 194-212. DOI: org/10.1016/j.apnum.2017.04.007. [27] J. Liu, M. S. Osman, W. Zhu et al., Different complex wave structures described by the hirota equation with variable coefficients in inhomogeneous optical fibers, Applied Physics B, 2019, 125: 175, 1-9. Https://doi.org/10.1007/s00340-019-7287-8. [28] S. Liu, Z. Fu, S. Liu and et al, Jacobi elliptic function expansion method and periodic wave solutions of nonlinear wave equations, Phys. Lett. A, 2001, 289, 69-74. DOI: org/10.1016/S0375-9601(01)00580-1. [29] D. Lu, M. Osman and M. M. A. e. a. Khater, Analytical and nu merical simulations for the kinetics of phase separation in iron (fe-cr x (x=mo, cu)) based on ternary alloys, Physica A, 2020, 537, 122634. Https://doi.org/10.1016/j.physa.2019.122634. doi: 10.1016/j.physa.2019.122634 [30] D. Lu, K. U. Tariq, M. Osman and et al, New analytical wave structures for the (3+1)-dimensional kadomtsev-petviashvili and the generalized boussi nesq models and their applications, Results in Physics, 2019, 14, 102491. Https://doi.org/10.1016/j.rinp.2019.102491. doi: 10.1016/j.rinp.2019.102491 [31] J. Lu, New exact solutions for kudryashov-sinelshchikov equation, Advances in difference equations, 2018, 374. DOI:org/10.1186/s13662-018-1769-6. [32] V. G. Makhankov, On stationary solutions of the schrödinger equation with a self-consistent potential satisfying boussinesq's equation, Phys. Lett. A, 1974, 50, 42-44. DOI:org/10.1016/0375-9601(74)90344-2. [33] W. Malfielt and W. Hereman, The tanh method: I. exact solutions of nonlinear evolution and wave equations, Physica Scripta, 1996, 54(6), 563-568. DOI: 10.1088/0031-8949/54/6/003. [34] V. B. Matveev and M. A. Salle, Darboux transformations and solitons, Springer, 1991. [35] A. A. Mohannad and M. Can, Painlevé annlysis and symmetries of the hirota satsuma equation, Journal of Nonlinear Mathematical Physics, 1996, 3, 152- 155. DOI: 10.2991/jnmp.1996.3.1-2.15. [36] M. Osman, B. Ghanbari and J. Machado, New complex waves in nonlinear optics based on the complex ginzburg-landau equation with kerr law nonlinearity, Eur. Phys. J. Plus, 2019, 134, 20. Https://doi.org/10.1140/epjp/i2019-12442-4. doi: 10.1140/epjp/i2019-12442-4 [37] M. Osman, D. Lub, M. Khater and R. Attia, Complex wave structures for abundant solutions related to the complex ginzburg-landau model, Optik, 2019, 192, 162927. Https://doi.org/10.1016/j.ijleo.2019.06.027. doi: 10.1016/j.ijleo.2019.06.027 [38] M. Osman, J. Machado and D. Baleanu, On nonautonomous complex wave solutions described by the coupled schrödinger-boussinesq equation with variable-coefficients, Optical and Qquantum Electronics, 2018, 52, 73. DOI: 10.1007/s11082-018-1346-y. [39] M. S. Osman, New analytical study of water waves described by coupled fractional variant boussinesq equation in fluid dynamics, Pramana-J. Phys., 2019, 93, 26. Https://doi.org/10.1007/s12043-019-1785-4. doi: 10.1007/s12043-019-1785-4 [40] M. S. Osman, M. Inc, J. Liu and et al, Different wave structures and stability analysis for the generalized (2+1)- dimensional camassa-holm-kadomtsev-petviashvili equation, Physica Scripta, 2019, 1-15. Https://doi.org/10.1088/1402-4896/ab52c1. doi: 10.1088/1402-4896/ab52c1 [41] M. S. Osman, K. U. Tariq, A. Bekir and et al, Investigation of soliton solutions with different wave structures to the (2 + 1)-dimensional heisenberg ferromagnetic spin chain equation, Commun. Theor. Phys., 2020, 72, 035002. Https://doi.org/10.1088/1572-9494/ab6181. doi: 10.1088/1572-9494/ab6181 [42] M. S. Osman and A. M. Wazwaz, A general bilinear form to generate different wave structures of solitons for a (3+1)-dimensional boiti-leon-manna-pempinelli equation, Math Meth Appl Sci, 2019, 1-7. Https://doi.org/10.1002/mma.5721. doi: 10.1002/mma.5721 [43] M. Osmana, D. Lu and M. M. Khater, A study of optical wave propagation in the nonautonomous schrödinger-hirota equation with power-law nonlinearity, Results in Physics, 2019, 13, 102157. Https://doi.org/10.1016/j.rinp.2019.102157. [44] H. Rezazadeh, M. Osman, M. Eslami and et al, Hyperbolic rational solutions to a variety of conformable fractional boussinesq-like equations, Nonlinear Engineering, 2019, 8, 224-230. Https://doi.org/10.1515/nleng-2018-0033. doi: 10.1515/nleng-2018-0033 [45] P. A. Robinson, D. L. Newman and M. V. Goldman, Three-dimensional strong langmuir turbulence and wave collapse, Phys. Rev. Lett., 1988, 61, 702-705. DOI: org/10.1103/PhysRevLett.61.702. [46] W. Rui, Applications of homogenous balanced principle on investigating exact solutions to a series of time fractional nonlinear pdes, Communications in Nonlinear Science and Numerical Simulation, 2017, 47, 253-266. DOI:org/10.1016/j.cnsns.2016.11.018. [47] S. Saha Ray, New double periodic exact solutions of the coupled schrödinger-boussinesq equations describing physical processes in laser and plasma physics, Chinese Journal of Physics, 2017, 55(5), 2039-2047. DOI: org/10.1016/j.cjph.2017.08.022. [48] A. R. Seadawy, W. Amer and A. Sayed, Stability analysis for traveling wave solutions of the olver and fifth-order kdv equations, Journal of Applied Mathematics, 2014, 839485(2014), 1-11. DOI: org/10.1155/2014/839485. [49] T. H. Stix, Waves in Plasmas, American Institute of Physics, NewYork. [50] C. Sulem and P. L. Sulem, The Nonlinear Schrödinger Equation: Self-focusing and Wave Collapse, Springer, 1999. [51] M. Wang and X. Li, Applications of f-expansion to periodic wave solutions for a new hamiltonian amplitude equation, Chaos Solitons Fract., 2005, 24, 1257-1268. DOI:org/10.1016/j.chaos.2004.09.044. [52] M. Wang, Y. Zhou and Z. Li, Applications of a homogeneous balance method to exact solutions of nonlinear equations in mathematical physics, Phys. Lett. A, 1996, 216, 67-75. DOI: org/10.1016/0375-9601(96)00283-6. [53] A. M. Wazwaz, Distinct variants of the kdv equation with compact and noncompact structures, Appl. Math. Comput., 2004, 150, 365-377. DOI: org/10.1016/S0096-3003(03)00238-8. [54] A. M. Wazwaz, Generalized solitonary and periodic solutions for nonlinear partial differential equations by the exp-function method, Nonlinear Dyn., 2008, 52, 1-9. DOI: org/10.1007/s11071-007-9250-1. [55] A. M. Wazwaz, Partial differential equations and solitary waves theory, Springer, 2009. [56] J. Weiss, M. Tabor and G. Carnevale, The painlev́ property for partial differential equations, Journal of Mathematical Physics, 1983, 24, 522-526. DOI:org/10.1063/1.525721. [57] N. Yajima and J. Satsuma, Soliton solutions in a diatomic lattice system, Progress of Theoretical Physics Supplements, 1979, 62, 370-378. DOI: org/10.1143/PTP.62.370. [58] Z. Yu, S. Jing, W. Zhang and et al, Simulation of the beam extraction from the triode system in small sealed tagged neutron tube, OptikInternational Journal for Light and Electron Optics, 2019, 181, 914-922. Https://doi.org/10.1016/j.ijleo.2018.12.166. doi: 10.1016/j.ijleo.2018.12.166 [59] V. E. Zakharov, Collapse of langmuir waves, Soviet Physics JETP, 1972, 35, 908-914. DOI: jetp.ac.ru/cgi-bin/dn/e-035-05-0908.pdf. [60] J. Zhang, M. Wang and X. Li, The subsidiary ordinary differential equations and the exact solutions of the higher order dispersive nonlinear schrödinger equation, Phys. Lett. A, 2006, 357, 188-195. DOI: org/10.1016/j.physleta.2006.03.081. [61] S. Zhang and Z. Li, New explicit exact solutions to nonlinearly coupled schrödinger-kdv equations(in chinese), ACTA PHYSICA, 2002, 51(10), 2197-2201. [62] X. Zhang and Y. Chen, General high-order rogue waves to nonlinear schrödinger-boussinesq equation with the dynamical analysis, Nonlinear Dyn., 2018, 93, 2169-2184. DOI: org/10.1007/s11071-018-4317-8. -
-
-
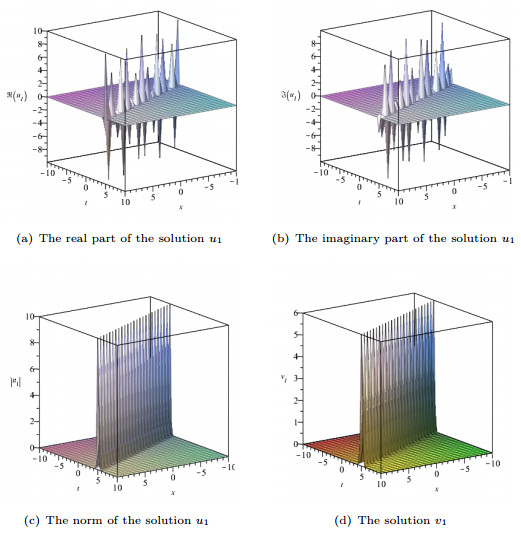
Figure 1. The real part of the solution
$ u_1(x, t) $ as shown in (a), the imaginary part of the solution$ u_1(x, t) $ as shown in (b), the norm of the solution$ u_1(x, t) $ as shown in (c), and the solution$ v_1(x, t) $ as shown in (d). -
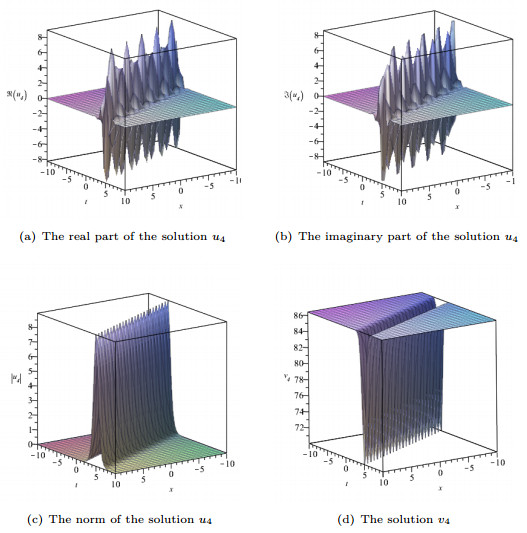
Figure 2. The real part of the solution
$ u_4(x, t) $ as shown in (a), the imaginary part of the solution$ u_4(x, t) $ as shown in (b), the norm of the solution$ u_4(x, t) $ as shown in (c), and the solution$ v_4(x, t) $ as shown in (d). -
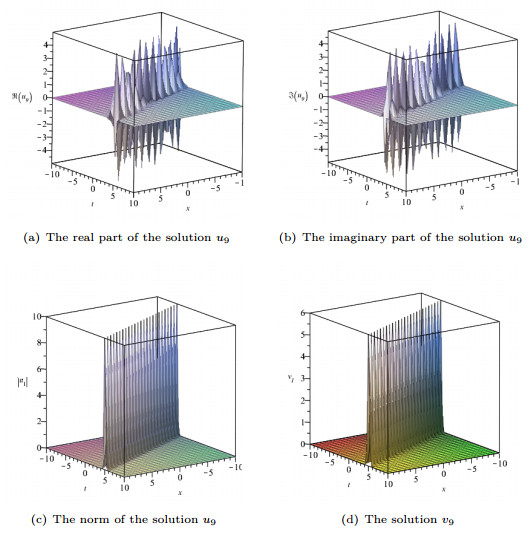
Figure 3. The real part of the solution
$ u_9(x, t) $ as shown in (a), the imaginary part of the solution$ u_9(x, t) $ as shown in (b), the norm of the solution$ u_9(x, t) $ as shown in (c), and the solution$ v_9(x, t) $ as shown in (d).




 DownLoad:
DownLoad: