| Citation: | Ping Liu, Yonghong Fan, Linlin Wang. EXISTENCE AND MULTIPLICITY OF POSITIVE PERIODIC SOLUTIONS FOR A CLASS OF SECOND ORDER DAMPED FUNCTIONAL DIFFERENTIAL EQUATIONS WITH MULTIPLE DELAYS[J]. Journal of Applied Analysis & Computation, 2021, 11(2): 798-809. doi: 10.11948/20190421 |
EXISTENCE AND MULTIPLICITY OF POSITIVE PERIODIC SOLUTIONS FOR A CLASS OF SECOND ORDER DAMPED FUNCTIONAL DIFFERENTIAL EQUATIONS WITH MULTIPLE DELAYS
-
Abstract
By using the Krasnoselskii fixed point theorem, sufficient conditions are obtained for the existence and multiplicity of positive periodic solutions for a class of second order damped functional differential equations with multiple delays. Our results are a further expansion of the previous research results.
-
Keywords:
- Periodic solutions /
- Green's function /
- Krasnoselskii fxed point
-

-
References
[1] Z. Cheng and F. Li, Positive periodic solutions for a kind of second-order neutral differential equations with variable coefcient and delay, Mediterr. J. Math., 2018, 15(3), 134–152. doi: 10.1007/s00009-018-1184-y [2] J. Chu, N. Fan and P. J. Torres, Periodic solutions for second order singular damped differential equations, J. Math. Anal. Appl., 2012, 388(2), 665–675. doi: 10.1016/j.jmaa.2011.09.061 [3] J. Chu, X. Lin, D. O. Regan et al., Multiplicity of positive solutions to second order differential equations, Bull. Austral. Math. Soc., 2006, 73(02), 175–182. doi: 10.1017/S0004972700038764 [4] K. Deimling, Nonlinear Functional Analysis, Springer-Verlag, New York, 1985. [5] H. Gabsi, A. Ardjouni and A. Djoudi, Existence of positive periodic solutions of nonlinear neutral differential systems with variable delays, 2018, 64, 83–97. [6] D. Guo and V. Lakshmikantham, Nonlinear Problems in Abstract Cones, Academic Press, New York, 1988. [7] R. Hakl and P. J. Torres, Maximum and antimaximum principles for a second order differential operator with variable codfcients of indefnite sign, Appl. Math. Comput., 2011, 217(19), 7599–7611. [8] J. K. Hale, Theory of Functional Differential Equations, Springer-Verlag, New York, 1977. [9] E. Hernández and S. Trofmchuk, Traveling waves solutions for partial neutral differential equations, Journal of Mathematical Analysis and Applications, 2020, 481(1), Article ID 123458. doi: 10.1016/j.jmaa.2019.123458 [10] D. Jiang, J. J. Nieto and W. Zuo, On monotone method for frst and second order periodic boundary value problems and periodic solutions of functional differential equations, J. Math. Anal. Appl., 2004, 289(2), 691–699. doi: 10.1016/j.jmaa.2003.09.020 [11] S. Kang and S. Cheng, Periodic solution for second order periodic differential equations under scalable control, Appl. Math. Comput., 2012, 218(18), 9138– 9146. [12] Y. Kuang, Delay Differential Equations with Applications in Population Dynamics, Academic Press, New York, 1993. [13] Q. Li and Y. Li, On the existence of positive periodic solutions for second-order functional differential equations with multiple delays, Abstr. Appl. Anal., 2012, Article ID 929870. [14] B. Mansouri, A. Ardjouni and A. Djoudi, Periodicity and continuous dependence in iterative differential equations, Rendiconti del Circolo Matematico di Palermo Series 2, 2019. DOI: 10.1007/s12215-019-00420-5. [15] M. I. Muminov, On the method of fnding periodic solutions of second-order neutral differential equations with piecewise constant arguments, Advances in Difference Equations, 2017, 336, 1–17. [16] H. V. Ngo, Existence results for extremal solutions of interval fractional functional integro-differential equations, Fuzzy Sets and Systems, 2018, 347(15), 29–53. [17] Z. Sabir, H. A. Wahab, M. Umar et al., Stochastic numerical approach for solving second order nonlinear singular functional differential equation, Applied Mathematics and Computation, 2019, 363(15), Article ID 124605. [18] P. J. Torres, Existence of one-signed periodic solutions of some second-order differential equations via a Krasnoselskii fxed point theorem, J. Differential Equations, 2003, 190(2), 643–662. doi: 10.1016/S0022-0396(02)00152-3 [19] C. Tunc and S. Erdur, New qualitative results for solutions of functional differential equations of second order, Discrete Dynamics in Nature and Society, 2018, DOI: 10.1155/2018/3151742. [20] N. Wang, Existence and uniqueness of periodic solutions for a kind of secondorder neutral functional differential equation with delays, Advances in Mathematical Physics, 2017, Article ID 9591087. [21] Y. Wu, Existence nonexistence and multiplicity of periodic solutions for a kind of functional differential equation with parameter, Nonlinear Anal., 2009, 70(1), 433–443. doi: 10.1016/j.na.2007.12.011 -
-
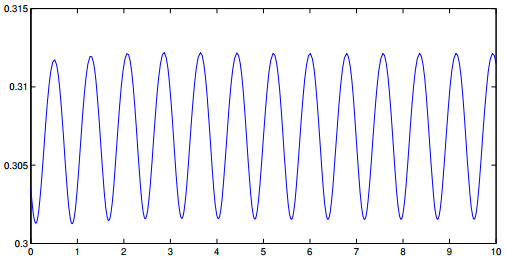
- Figure 1. The numerical simulation of Example 4.1.




 DownLoad:
DownLoad: