| Citation: |
Chuanying Zhang, Ranchao Wu, Mengxin Chen. HOPF BIFURCATION IN A DELAYED PREDATOR-PREY SYSTEM WITH GENERAL GROUP DEFENCE FOR PREY[J]. Journal of Applied Analysis & Computation, 2021, 11(2): 810-840. doi: 10.11948/20200011
|
HOPF BIFURCATION IN A DELAYED PREDATOR-PREY SYSTEM WITH GENERAL GROUP DEFENCE FOR PREY
-
Abstract
In this paper, a delayed predator-prey system with group defence for prey is investigated. Firstly, in the absence of spatial diffusion and time delay, the stability of positive equilibrium and existence of the Hopf bifurcation are investigated, as well as the direction of the Hopf bifurcation, which is determined by applying the first Lyapunov number. Then, the occurrence of the Hopf bifurcation in the diffusion-driven delayed system is further explored. By using the center manifold reduction and the normal form theorem, the conditions ensuring the occurrence of Hopf bifurcation, its direction and its stability are formulated in terms of different parameters. Finally, some numerical simulations are carried out to verify the theoretical results and the existence of the homogeneous periodic solution is exhibited by setting different values of parameters. Moreover, stable temporal periodic solutions and spatially inhomogeneous periodic solutions are identified from the numerical simulations. The obtained results are also explained and discussed from the practical point of view.
-
Keywords:
- Stability /
- hopf bifurcation /
- time delay /
- group defense
-
-
References
[1] J. F. Andrews, A mathematical model for the continuous culture of microorganisms utilizing inhibitory substrates, Biotechnol. Bioeng., 1968, 10, 707–723. doi: 10.1002/bit.260100602 [2] R. Arditi and L. R. Ginzburg, Coupling in predator-prey dynamics: ratiodependence, J. Theor. Biol., 1989, 139, 311–326. doi: 10.1016/S0022-5193(89)80211-5 [3] V. Ajraldi, M. Pittavino and E. Venturino, Modeling herd behavior in population systems, Nonlinear Anal. : RWA, 2011, 12, 2319–2338. doi: 10.1016/j.nonrwa.2011.02.002 [4] J. R. Beddington, Mutual interference between parasites or predators and its effect on searching efficiency, J. Anim. Ecol., 1975, 44, 331–340. doi: 10.2307/3866 [5] J. Cao and R. Yuan, Bifurcation analysis in a modifed Lesile-Gower model with Holling type Ⅱ functional response and delay, Nonlinear Dyn., 2016, 84, 1341–1352. doi: 10.1007/s11071-015-2572-5 [6] B. Chakraborty and N. Bairagi, Complexity in a prey-predator model with prey refuge and diffusion, Ecol. Complex., 2019, 37, 11–23. doi: 10.1016/j.ecocom.2018.10.004 [7] M. Chen, R. Wu, B. Liu and L. Chen, Spatiotemporal dynamics in a ratiodependent predator-prey model with time delay near the Turning-Hopf bifurcation point, Commun. Nonlinear Sci. Numer. Simulat., 2019, 77, 141–167. doi: 10.1016/j.cnsns.2019.04.024 [8] S. Djilali, Impact of prey herd shape on the predator-prey interaction, Chaos Soliton Fract., 2019, 120, 139–148. doi: 10.1016/j.chaos.2019.01.022 [9] H. I. Freefman and V. S. H. Rao, The trade-off between mutual interference and time lag in predator-prey-systems, Bull. Math. Biol., 1983, 45, 991–1004. doi: 10.1016/S0092-8240(83)80073-1 [10] W. Gao and B. Dai, Dynamics of a predator-prey model with delay and fear effect, J. Nonlinear Model. Anal., 2019, 1, 57–72. [11] C. S. Holling, The functional response of predators to prey density and its role in mimicry and population regulation, Mem. Entomol. Soc. Can., 1965, 97, 1–60. doi: 10.4039/Ent971-1 [12] B. D. Hassard, N. D. Kazarinoff and Y. Wan, Theory and Applications of Hopf bifurcation, Cambridge University Press, Cambridge-New York, 1981. [13] R. Han and B. Dai, Cross-diffusion induced Turing instability and amplitude equation for a toxic-phytoplankton-zooplankton model with nonmonotonic functional response, Int. J. Bifurcat. Chaos, 2017, 27, 1750088. doi: 10.1142/S0218127417500882 [14] S. Kumar and H. Kharbanda, Chaotic behavior of predator-prey model with group defense and non-linear harvesting in prey, Chaos Soliton Fract., 2019, 119, 19–28. Hopf bifurcation 83 doi: 10.1016/j.chaos.2018.12.011 [15] S. Kayan and H. Merdan, An algorithm for Hopf bifurcation analysis of a delayed reaction-diffusion model, Nonlinear Dyn., 2017, 89, 345–366. doi: 10.1007/s11071-017-3458-5 [16] A. J. Lotka, Elements of Physical Biology, Williams and Wilkins, New York, 1925. [17] Y. Lv, Y. Pei and R. Yuan, Hopf bifurcation and global stability of a diffusive Gause-type predator-prey models, Comput. Math. Appl., 2016, 72, 2620–2635. doi: 10.1016/j.camwa.2016.09.022 [18] B. Liu, R. Wu and L. Chen, Turing-Hopf bifurcation analysis in a superdiffusive predator-prey model, Chaos, 2018, 28, 113118. doi: 10.1063/1.5055711 [19] D. Melchionda, E. Pastacaldi, C. Perria and M. Banerjee, Social behaviorinduced multistability in minimal competitive ecosystems, J. Theor. Biol., 2018, 439, 24–38. doi: 10.1016/j.jtbi.2017.11.016 [20] Z. Ma, J. Liu and J. Yue, Spatiotemporal dynamics induced by delay and diffusion in a predator-prey model with mutual interference among the predator, Comput. Math. Appl., 2018, 75, 3488–3507. doi: 10.1016/j.camwa.2018.02.012 [21] R. M. May, Time-delay versus stability in population models with two and three trophic levels, Ecology, 1973, 54, 315–325. doi: 10.2307/1934339 [22] L. Perko, Differential Equations and Dynamical Systems. third edition, Springer-Verlag, New York, 2001. [23] S. Sun, C. Guo and C. Qin, Dynamic behaviors of a modifed predator-prey model with state-dependent impulsive effects, Adv. Differ. Equ., 2016, 50. doi: 10.1186/s13662-015-0735-9 [24] H. L. Smith, An Introduction to Delay Differential Equations with Sciences Applications to the Life, Springer, New York, 2010. [25] X. Tang, H. Jiang and Z. Deng, Delay induced subcritical Hopf bifurcation in a diffusive predator-prey model with herd behavior and hyperbolic mortality, J. Appl. Anal. Comput., 2017, 7, 1385–1401. [26] C. Tian and S. Ruan, Pattern formation and synchronism in an allelopathic plankton model with delay in a network, SIAM. J. Appl. Dyn. Syst., 2019, 18, 531–557. doi: 10.1137/18M1204966 [27] V. Volterra, Fluctuations in the abundance of a species considered mathematically, Nature, 1926, 118, 558–560. doi: 10.1038/118558a0 [28] E. Venturino and S. Petrovskii, Spatiotemporal behavior of a prey-predator system with a group defense for prey, Ecol. Complex., 2013, 14, 37–47. doi: 10.1016/j.ecocom.2013.01.004 [29] F. Wei, C. Wang and S. Yuan, Spatial dynamics of a diffusive predator-prey modek with Leslie-Gower functional response and strong Allee effect, J. Nonlinear Model. Anal., 2020, 2, 267–285. [30] R. Wu, M. Chen and B. Liu, Hopf bifurcation and Turing instability in a predator-prey model with Michaelis-Menten functional response, Nonlinear Dyn., 2018, 91, 2033–2047. doi: 10.1007/s11071-017-4001-4 [31] J. Wu, Theory and Applications of Partial Functional Differential Equations, Springer Berlin, 1996. [32] Z. Xu and Y. Song, Bifurcation analysis of a diffusive predator-prey system with a herd behavior and quadratic mortality, Math. Methods Appl. Sci., 2015, 38, 2994–3006. doi: 10.1002/mma.3275 [33] C. Xu, S. Yuan and T. Zhang, Global dynamics of a predator-prey model with defense mechanism for prey, Appl. Math. Lett., 2016, 62, 42–8. doi: 10.1016/j.aml.2016.06.013 [34] H. Yin and X. Wen, Hopf bifurcation of a diffusive Gause-type predator-prey model induced by time fractional-order derivatives, Math. Methods Appl. Sci., 2018, 41, 5178–5189. doi: 10.1002/mma.5066 [35] H. Zhu and X. Zhang, Dynamics and patterns of a diffusive prey-predator system with a group defense for prey, Discrete Dyn. Nat. Soc., 2018, 6519696. -
-
Figures(9)
Export File
Citation
Chuanying Zhang, Ranchao Wu, Mengxin Chen. HOPF BIFURCATION IN A DELAYED PREDATOR-PREY SYSTEM WITH GENERAL GROUP DEFENCE FOR PREY[J]. Journal of Applied Analysis & Computation, 2021, 11(2): 810-840. doi: 10.11948/20200011
Format
Content
DownLoad:
-
Figure 1. The equilibrium
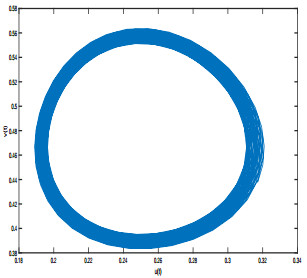
$ E_* $ is locally asymptotically stable. - Figure 2. The periodic solution bifurcated from the Hopf bifurcation is stable
-
Figure 3. Solutions
$ u(x, t) $ and$ v(x, t) $ with diffusion and different aggregation efficiency$ \alpha $ . The Hopf bifurcation could exist in the following situations: (i)$ \alpha = 0.2 $ (top panel), (ii)$ \alpha = 0.5 $ (middle panel), (iii)$ \alpha = 0.75 $ (bottom panel), other parameters could refer to (i-iii) in Remark 2.2. Here choose the initial values$ u(x, 0) = u_*-0.001\cos2x, \; v(x, 0) = u_*-0.001\cos2x $ . -
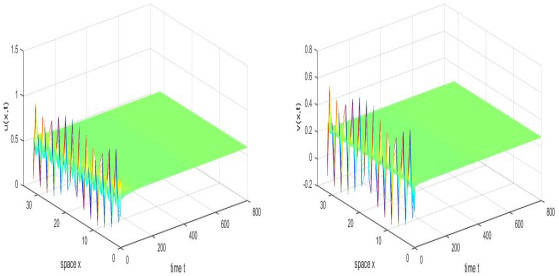
Figure 4.
$ E_* = (0.5905, 0.2687) $ is locally asymptotically stable, where$ \tau = 1.34 $ and initial condition is$ (u(x, 0), v(x, 0)) = (0.5905+0.5\cos(2x), 0.2687+0.4\cos(2x)) $ . -
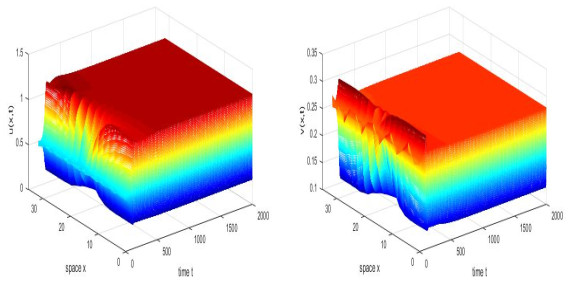
Figure 5. When
$ \alpha = 0.2, $ the bifurcating periodic solutions are stable, where$ \tau = 1.48 $ and initial condition is$ (u(x, 0), v(x, 0)) = (0.5905+0.02\cos(2x), 0.2687+0.02\cos(2x)) $ . -
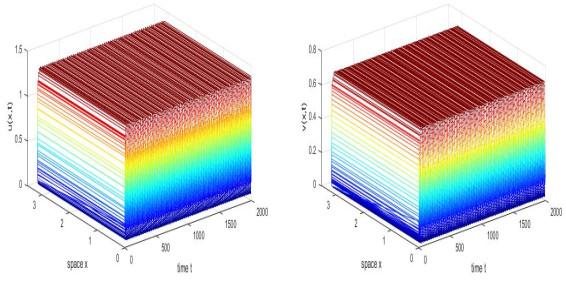
Figure 6. When
$ \alpha = 0.5, $ the bifurcating periodic solutions are stable, where$ \tau = 1.29 $ and initial condition is$ (u(x, 0), v(x, 0)) = (0.4624+0.5\cos(2x), 0.3656+0.5\cos(2x)) $ . -
Figure 7. When
$ \alpha = 0.7, $ the bifurcating periodic solutions are stable, where$ \tau = 1.5 $ and initial condition is$ (u(x, 0), v(x, 0)) = (0.663-0.02\cos(2x), 0.2979-0.02\cos(2x)) $ . -
Figure 8. For system (1.4), there exist quasi periodic solution, where
$ \alpha = 0.2, \; \tau = 1.2942 $ and initial condition is$ (u(x, 0), v(x, 0)) = (0.4624+0.005\cos(5x), 0.3656+0.05\cos(5x)) $ . -
Figure 9. For system (1.4), the spatially inhomogeneous bifurcating periodic solution are stable, where
$ \alpha = 0.93, \; \tau = 2.08 $ and initial condition is$ (u(x, 0), v(x, 0)) = (0.5601-0.2\cos(2x), 0.4224-0.2\cos(2x)) $ .