| Citation: |
Hong-Yi Zhang, Yu-Feng Zhang. DARBOUX TRANSFORMATIONS, MULTISOLITONS, BREATHER AND ROGUE WAVE SOLUTIONS FOR A HIGHER-ORDER DISPERSIVE NONLINEAR SCHRÖDINGER EQUATION[J]. Journal of Applied Analysis & Computation, 2021, 11(2): 892-902. doi: 10.11948/20200080
|
DARBOUX TRANSFORMATIONS, MULTISOLITONS, BREATHER AND ROGUE WAVE SOLUTIONS FOR A HIGHER-ORDER DISPERSIVE NONLINEAR SCHRÖDINGER EQUATION
-
Abstract
In this paper, dynamic of a higher-order dispersive nonlinear Schrö-dinger equation is investigated. Firstly, we obtain the determinant representation of the N-fold Darboux transformations of the Schrödinger equation. Then based on the above analysis, we get the one-soliton, two-soliton and the breather wave solution. Furthermore, the first-order rogue wave is derived by means of a Taylor expansion of the breather wave. Finally, by selecting some special parameters and drawing the 3-D and 2-D graphs to better describe the dynamic traits of those solutions.
-
-
References
[1] A. Abdeljabbar, W. Ma and A. Yildirim, Determinant solutions to a (3+1)-dimensional generalized KP equation with variable coefficients, Chinese Annals of Mathematics, Series B, 2012, 33(5), 641-650. doi: 10.1007/s11401-012-0738-8 [2] N. Akhmediev, A. Ankiewicz and J. M. Soto-Crespo, Rogue waves and rational solutions of the nonlinear Schrödinger equation, Physical Review E, 2009, 80(2), 026601. doi: 10.1103/PhysRevE.80.026601 [3] M. Alam, M. Rahman, R. Islam et al., Application of the new extended (G'/G)-expansion method to find exact solutions for nonlinear partial differential equation, Computational Methods for Differential Equations, 2015, 3(1), 59-69. [4] H. M. Baskonus, H. Bulut and T.A. Sulaiman, New complex hyperbolic structures to the lonngren-wave equation by using sine-gordon expansion method, Applied Mathematics and Nonlinear Sciences, 2019, 4(1), 129-138. doi: 10.2478/AMNS.2019.1.00013 [5] H. M. Baskonus, H. Bulut and A. Atangana, On the complex and hyperbolic structures of the longitudinal wave equation in a magneto-electro-elastic circular rod, Smart Materials and Structures, 2016, 25(3), 035022. doi: 10.1088/0964-1726/25/3/035022 [6] J. Chen, Y. Chen, B. Feng et al., Rational solutions to two- and one-dimensional multicomponent Yajima-Oikawa systems, Physics Letters A, 2015, 379(24-25), 1510-1519. doi: 10.1016/j.physleta.2015.02.040 [7] S. K. El-Labany, W. M. Moslem, E. I. El-Awady et al., Nonlinear dynamics associated with rotating magnetized electron-positron-ion plasmas, Physics Letters A, 2010, 375(2), 159-164. [8] V. Efimov, P. McClintock, A. Ganshin et al., Experiments on Rogue Waves in Superfluid 4He. 2009. [9] B. Guo and L. Ling, Riemann-Hilbert approach and N-soliton formula for coupled derivative Schrödinger equation, Journal of Mathematical Physics, 2012, 53(7), 073506. doi: 10.1063/1.4732464 [10] B. Guo, L. Ling and Rogue Wave, Breathers and Bright-Dark-Rogue Solutions for the Coupled Schrödinger Equations, Chinese Physics Letters, 2011, 28(11). [11] J. He, H. Zhang, L. Wang et al., A generating mechanism for higher order rogue waves, Physical Review E, 2013, 87(5-1), 052914. [12] C. M. Khalique and I. E. Mhlanga, Travelling waves and conservation laws of a (2+1)-dimensional coupling system with Korteweg-de Vries equation, Applied Mathematics and Nonlinear Sciences, 2018, 3(1), 241-254. doi: 10.21042/AMNS.2018.1.00018 [13] D. J. Kaup and A. C. Newell, An exact solution for a derivative nonlinear Schrödinger equation, Journal of Mathematical Physics, 1978, 19(4), 798. doi: 10.1063/1.523737 [14] M. Lakshmanan, K. Porsezian and M. Daniel, Effect of discreteness on the continuum limit of the Heisenberg spin chain, Physics Letters A, 1988, 133(9), 483-488. doi: 10.1016/0375-9601(88)90520-8 [15] V. B. Matveev and M. A. Salle, Darboux Transformations and Solitons, Springer, Berlin-Heidelberg, 1991. [16] G. Neugebauer and R. Meinel, General N-soliton solution of the AKNS class on arbitrary background, Physics Letters A, 1984, 100(9), 467-470. doi: 10.1016/0375-9601(84)90827-2 [17] Z. Pinar, Analytical studies for the Boiti-Leon-Monna-Pempinelli equations with variable and constant coefficients, Asymptotic Analysis, 2019, 1-9. [18] K. Porsezian, M. Daniel and M. Lakshmanan, On the integrability aspects of the one-dimensional classical continuum isotropic biquadratic Heisenberg spin chain, Journal of Mathematical Physics, 1992, 33(5), 1807-1816. doi: 10.1063/1.529658 [19] N. V. Priya, M. Senthilvelan and M. Lakshmanan, Akhmediev breathers, Ma solitons and general breathers from rogue waves: A case study in Manakov system, Physical Review E, 2013, 88(2), 022918. doi: 10.1103/PhysRevE.88.022918 [20] Z. Qiao, A new completely integrable Liouville's system produced by the Kaup-Newell eigenvalue problem, Journal of Mathematical Physics, 1993. [21] Z. Qiao, A hierarchy of nonlinear evolution equations and finite-dimensional involutive systems, Journal of Mathematical Physics, 1994, 35(6), 2971-2977. doi: 10.1063/1.530882 [22] T. A. Sulaiman, A. Yokus, N. Gulluoglu et al., Regarding the numerical solutions of the Sharma-Tasso-Olver equation, Itm Web of Conferences, 2018, 22. [23] E. K. Sklyanin, Method of the inverse scattering problem and the nonlinear quantum Schrödinger equation, Soviet Physics Doklady, 1979, 24. [24] X. Wang, Y. Li and Y. Chen, Generalized Darboux transformation and localized waves in coupled Hirota equations, Wave Motion, 2014, 51(7), 1149-1160. doi: 10.1016/j.wavemoti.2014.07.001 [25] L. Wang, K. Porsezian and J. He, Breather and rogue wave solutions of a generalized nonlinear Schrödinger equation, Physical Review E, 2013, 87(5), 053202. doi: 10.1103/PhysRevE.87.053202 [26] L. Wang, K. Porsezian and J. He, Breather and rogue wave solutions of a generalized nonlinear Schrödinger equation, Physical Review E, 2013, 87(5), 053202. doi: 10.1103/PhysRevE.87.053202 [27] L. Xu and J. Zhang, Exact solutions to two higher order nonlinear Schrödinger equations, Chaos, Solitons & Fractals, 2007, 31(4), 937-942. [28] A. Yokus, H. M. Baskonus, T. A. Sulaiman et al., Numerical simulation and solutions of the two-component second order KdV evolutionary system, Numerical Methods for Partial Differential Equations, 2018, 34(1), 211-227. [29] H. Zhang, B. Tian, X. Meng et al., Conservation laws, soliton solutions and modulational instability for the higher-order dispersive nonlinear Schrödinger equation, The European Physical Journal B, 2009, 72(2), 233. [30] J. Zhang, L. Wang and C. Liu, Superregular breathers, characteristics of nonlinear stage of modulation instability induced by higher-order effects, Proceedings of the Royal Society A Mathematical Physical and Engineering Sciences, 2017, 473(2199), 20160681. doi: 10.1098/rspa.2016.0681 [31] Y. Zhang, Q. Liu and Z. Qiao, Fifth-order b-family Novikov (FObFN) model with pseudo-peakons and multi-peakons, Modern Physics Letters B, 2019, 33(18), 1950205. doi: 10.1142/S0217984919502051 -
-
Figures(4)
Export File
Citation
Hong-Yi Zhang, Yu-Feng Zhang. DARBOUX TRANSFORMATIONS, MULTISOLITONS, BREATHER AND ROGUE WAVE SOLUTIONS FOR A HIGHER-ORDER DISPERSIVE NONLINEAR SCHRÖDINGER EQUATION[J]. Journal of Applied Analysis & Computation, 2021, 11(2): 892-902. doi: 10.11948/20200080
Format
Content
DownLoad:
-
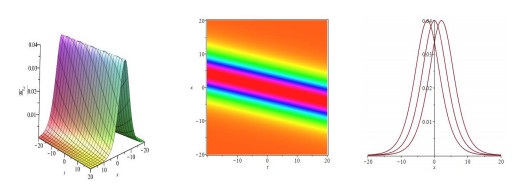
Figure 1. The one-soliton solution of the higher-order dispersive nonlinear Schrödinger equation with
$ \eta = 0.1,\xi = 0.05 $ and$ \tau = 1 $ : a three-dimensional plot, b density plot, c the two-dimensional plot at different$ t = -10 $ (left),$ t = 0 $ (middle),$ t = 10 $ (right). -
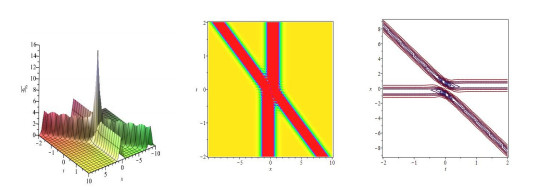
Figure 2. The two-soliton solution of the higher-order dispersive nonlinear Schrödinger equation with
$ \eta = 1,\xi = 1,\upsilon = 1,\theta = 0, $ and$ \tau = 1 $ : a three-dimensional plot, b density plot, c the contour plot. -
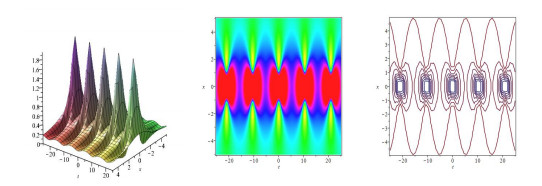
Figure 3. The first-order breather solution of higher-order dispersive nonlinear Schrödinger equation with
$ \eta = 0.2,\xi = 0,b = 1,c = 1, $ and$ \tau = 1 $ : a three-dimensional plot, b density plot, c the contour plot. -
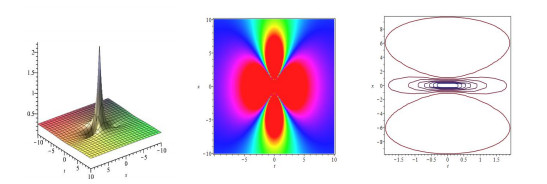
Figure 4. The first-order rogue wave solution of higher-order dispersive nonlinear Schrödinger equation with
$ \xi = 0,\eta = 0.5,a = 0,b = 1,c = 0.5, $ and$ \tau = 0.5 $ : a three-dimensional plot, b density plot, c the contour plot.