| Citation: |
Changjin Xu, Maoxin Liao, Peiluan Li, Shuai Yuan. NEW INSIGHTS ON BIFURCATION IN A FRACTIONAL-ORDER DELAYED COMPETITION AND COOPERATION MODEL OF TWO ENTERPRISES[J]. Journal of Applied Analysis & Computation, 2021, 11(3): 1240-1258. doi: 10.11948/20200087
|
NEW INSIGHTS ON BIFURCATION IN A FRACTIONAL-ORDER DELAYED COMPETITION AND COOPERATION MODEL OF TWO ENTERPRISES
-
Abstract
Over the past decades, many authors establish various kinds of competition and cooperation models of two enterprises to analyze the dynamic interaction. However, they are only concerned with integer-order differential equation models, while the reports on fractional-order ones are very rare. In this article, based on the earlier studies, we propose a new fractional-order delayed competition and cooperation model of two enterprises. Letting the delay be bifurcation parameter and analyzing the corresponding characteristic equation of involved model, we establish some new sufficient conditions to guarantee the stability and the existence of Hopf bifurcation of fractional-order delayed competition and cooperation model of two enterprises. The research indicates that different delays have different effect on the stability and Hopf bifurcation of involved model. The impact of the fractional order on the stability and Hopf bifurcation of involved model is displayed. To check the correctness of theoretical analysis, we implement some computer simulations.
-
-
References
[1] M. S. Abdelouahab, N. E. Hamri, J. Wang, Hopf bifurcation and chaos in fractional-order modified hybrid optical system, Nonlinear Dyn., 2012, 69(1-2), 275-284. doi: 10.1007/s11071-011-0263-4 [2] H. Bao, J. H. Park, J. Cao, Synchronization of fractional-order complex-valued neural networks with time delay, Neural Netw., 2016, 81, 16-28. doi: 10.1016/j.neunet.2016.05.003 [3] S. Bhalekar, V. D. Gejji, Chaos in fractional order financial delay system, Comput. Math. Appl., 2016, doi:10.1016/j.camwa.2016.03.009 [4] J. Chen, B. Chen, Z. Zeng, O(t-α)-synchronization and Mittag-Leffler synchronization for the fractional-order memristive neural networks with delays and discontinuous neuron activations, Neural Netw., 2018, 100, 10-24. doi: 10.1016/j.neunet.2018.01.004 [5] S. Chen, Y. Lou, J. Wei, Hopf bifurcation in a delayed reaction-diffusion-advection population model, J. Diff. Equat., 2018, 264(8), 5333-5359. doi: 10.1016/j.jde.2018.01.008 [6] S. Chen, J. Wei, Stability and bifurcation in a two variable delay model for circadian rhythm of neurospora crassa open archive, J. Math. Anal. Appl., 2014, 411(1), 381-394. doi: 10.1016/j.jmaa.2013.09.045 [7] W. Deng, C. Li, J. Lü, Stability analysis of linear fractional differential system with multiple time delays, Nonlinear Dyn., 2007, 48(4), 409-416. doi: 10.1007/s11071-006-9094-0 [8] A. S. Deshpande, V. D. Gejji, Y. V. Sukale, On Hopf bifurcation in fractional dynamical systems, Chaos, Solitons & Fractals, 2017, 98, 189-198. [9] S. Djilali, B. Ghanbari, S. Bentout, A. Mezouaghi, Turing-Hopf bifurcation in a diffusive mussel-algae model with time-fractional-order derivative, Chaos, Solitons & Fractals, 2020, 138, 109954. [10] Q. Feng, F. Meng, Traveling wave solutions for fractional partial differential equations arising in mathematical physics by an improved fractional Jacobi elliptic equation method, Math. Meth. Appl. Sci., 2017, 40(10), 3676-3686. doi: 10.1002/mma.4254 [11] S. Guo, S. Yan, Hopf bifurcation in a diffusive Lotka-Volterra type system with nonlocal delay effect, J. Diff. Equat., 2016, 260(1), 781-817. doi: 10.1016/j.jde.2015.09.031 [12] N. Hamdan, A. Kilicman, A fractional order SIR epidemic model for dengue transmission, Chaos, Solitons & Fractals, 2018, 114, 55-62. [13] C. Huang, Multiple scales scheme for bifurcation in a delayed extended van der Pol oscillator, Phys. A: Stat. Mech. Appl., 2018, 490, 643-652. doi: 10.1016/j.physa.2017.08.035 [14] C. Huang, J. Cao, Impact of leakage delay on bifurcation in high-order fractional BAM neural networks, Neural Netw., 2018, 98, 223-235. doi: 10.1016/j.neunet.2017.11.020 [15] C. Huang, J. Cao, M. Xiao, Hybrid control on bifurcation for a delayed fractional gene regulatory network, Chaos, Solitons & Fractals, 2016, 87, 19-29. [16] C. Huang, J. Cao, M. Xiao, A. Alsaedi, T. Hayat, Bifurcations in a delayed fractional complex-valued neural network, Appl. Math. Comput., 2017, 292, 210-227. [17] J. Huo, H. Zhao, L. Zhu, The effect of vaccines on backward bifurcation in a fractional order HIV model, Nonlinear Anal-Real., 2015, 26, 289-305. doi: 10.1016/j.nonrwa.2015.05.014 [18] J. Jian, P. Wan, Lagrange α-exponential stability and α-exponential convergence for fractional-order complex-valued neural networks, Neural Netw., 2017, 91, 1-10. doi: 10.1016/j.neunet.2017.03.011 [19] E. Kaslik, I. R. Rǎdulescu, Dynamics of complex-valued fractional-order neural networks, Neural Netw., 2017, 89, 39-49. doi: 10.1016/j.neunet.2017.02.011 [20] K. S. Kim, S. Kim, I. H. Jung, Hopf bifurcation analysis and optimal control of treatment in a delayed oncolytic virus dynamics, Math. Comput. Simul., 2018, 149, 1-16. doi: 10.1016/j.matcom.2018.01.003 [21] A. Kumar, V. Kumar, Performance analysis of optimal hybrid novel interval type-2 fractional order fuzzy logic controllers for fractional order systems, Exp. Syst. Appl., 2018, 93, 435-455. doi: 10.1016/j.eswa.2017.10.033 [22] L. Li, C. Zhang, X. Yan, Stability and Hopf bifurcation analysis for a two-enterprise interaction model with delays, Neurocomputing, Commun. Nonlinear Sci. Numer. Simul., 2016, 30(1-3), 70-83. doi: 10.1016/j.cnsns.2015.06.011 [23] N. Lekdee, S. Sirisubtawee, S. Koonprasert, Bifurcations in a delayed fractional model of glucose-insulin interaction with incommensurate orders, Adv. in Diff. Equat., 2019, 318, 22 pages. [24] M. Li, J. Wang, Exploring delayed Mittag-Leffler type matrix functions to study finite time stability of fractional delay differential equations, Appl. Math. Comput., 2018, 324, 254-265. [25] Y. Li, T. Zhang, Global asymptotical stability of a unique almost periodic solution for enterprise clusters based on ecology theory with time-varying delays and feedback controls, Commun. Nonlinear Sci. Numer. Simul., 2012, 17(2), 904-913. doi: 10.1016/j.cnsns.2011.05.036 [26] M. Liao, C. Xu, X. Tang, Dynamical behaviors for a competition and cooperation model of enterprises with two delays, Nonlinear Dyn., 2014, 75(1-2), 257-66. doi: 10.1007/s11071-013-1063-9 [27] M. Liao, C. Xu, X. Tang, Stability and Hopf bifurcation for a competition and cooperation model of two enterprises with delay, Commun. Nonlinear Sci. Numer. Simul., 2014, 19(10), 3845-3856. doi: 10.1016/j.cnsns.2014.02.031 [28] P. Liu, Y. Li, Permanence for a competition and cooperation model of enterprise cluster with delays and feedback controls, Electron. J. Diff. Equa., 2013, 2013(22), 1-9. [29] D. Matignon, Stability results for fractional differential equations with applications to control processing, Computational engineering in systems and application multi-conference, IMACS. In: IEEE-SMC Proceedings, Lille, 2; 1996. p. 963-8. France; July 1996. [30] A. S. Mohamadi, A. Pourabbas, S. M. Vaezpour, Periodic solutions of delay differential equations with feedback control for enterprise clusters based on ecology theory, J. Inequa. Appl., 2014, 306, 1-15. [31] I. Podlubny, Fractional Differential Equations, Academic Press, New York, 1999. [32] A. Pratap, R. Raja, C. Sowmiya, O. Bagdasar, G. Rajchakit, Robust generalized Mittag-Leffler synchronization of fractional order neural networks with discontinuous activation and impulses, Neural Netw., 2018, 103, 128-141. doi: 10.1016/j.neunet.2018.03.012 [33] K. Rajagopal, A. Karthikeyan, P. Duraisamy, R. Weldegiorgis, G. Tadesse, Bifurcation, Chaos and its control in a fractional order power system model with uncertaities, Asian J. Contr., 2018, 21(1), 1-10. [34] K. Rajagopal, A. Karthikeyan, A. Srinivasan, Bifurcation and chaos in time delayed fractional order chaotic memfractor oscillator and its sliding mode synchronization with uncertainties, Chaos, Solitons Fract., 2017, 103, 347-356. doi: 10.1016/j.chaos.2017.06.028 [35] R. Rakkiyappan, K. Udhayakumar, G. Velmurugan, J. Cao, A. Alsaedi, Stability and Hopf bifurcation analysis of fractional-order complex-valued neural networks with time delays, Adv. Diff. Equat., 2017, 225, 1-25. [36] T. Shen, J. Xin, J. Huang, Time-space fractional stochastic Ginzburg-Landau equation driven by Gaussian white noise, Stoch. Anal. Appl., 2018, 36(1), 103-113. [37] Y. Song, Spatio-temporal patterns of Hopf bifurcating periodic oscillations in a pair of identical tri-neuron network loops, Commun. Nonlinear Sci. Numer. Simul., 2012, 17(2), 943-952. doi: 10.1016/j.cnsns.2011.06.005 [38] A. G. Soriano-Sánchez, C. Posadas-Castillo, M. A. Platas-Garza, A. Arellano-Delgado, Synchronization and FPGA realization of complex networks with fractional-order Liu chaotic oscillators, Appl. Math. Comput., 2018, 332, 250-262. [39] B. Tao, M. Xiao, Q. Sun, J. Cao, Hopf bifurcation analysis of a delayed fractional-order genetic regulatory networks model, Neurocomput., 2018, 275, 677-686. doi: 10.1016/j.neucom.2017.09.018 [40] W. W. Teka, R. K. Upadhyay, A. Mondal, Spiking and bursting patterns of fractional-order Izhikevich model, Proceed. Commun. Nonlinear Sci. Numer. Simul., 2018, 56, 161-176. doi: 10.1016/j.cnsns.2017.07.026 [41] G. Velmurugan, R. Rakkiyappan, V. Vembarasan, J. Cao, A. Alsaedi, Dissipativity and stability analysis of fractional-order complex-valued neural networks with time delay, Neural Netw., 2017, 86, 42-53. doi: 10.1016/j.neunet.2016.10.010 [42] Y. Wang, J. Jiang, Existence and nonexistence of positive solutions for the fractional coupled system involving generalized p-Laplacian, Adv. Diff. Equat., 2017, 337, 1-19. [43] Y. Wang, L. Liu, Positive solutions for a class of fractional 3-point boundary value problems at resonance, Adv. Diff. Equa., 2017, 7, 1-13. doi: 10.1186/s13662-016-1062-5 [44] X. Wang, Z. Wang, J. Xia, Stability and bifurcation control of a delayed fractional-order eco-epidemiological model with incommensurate orders, J. Franklin Inst., 2019, 356(15), 8278-8295. doi: 10.1016/j.jfranklin.2019.07.028 [45] Z. Wang, X. Wang, Y. Li, X. Huang, Stability and Hopf bifurcation of fractional-order complex-valued single neuron model with time delay, Int. J. Bifur. Chaos, 2017, 27(13), 1750209. doi: 10.1142/S0218127417502091 [46] Z. Wang, Y. Xie, J. Lu, Y. Li, Stability and bifurcation of a delayed generalized fractional-order prey-predator model with interspecific competition, Appl. Math. Comput., 2019, 347, 360-369. [47] M. Xiao, G. Jiang, W. Zheng, S. Yan, Y. Wan, C. Fan, Bifurcation control od a fractional-order van der pol oscillator based on the state feedback, Asian J. Contr., 2015, 17(5), 1755-1766. [48] M. Xiao, W. Zheng, J. Lin, G. Jiang, L. Zhao, Fractional-order PD control at Hopf bifurcation in delayed fractional-order small-world networks, J. Franklin Inst., 2017, 354(17), 7643-7667. doi: 10.1016/j.jfranklin.2017.09.009 [49] C. Xu, Local and global Hopf bifurcation analysis on simplified bidirectional associative memory neural networks with multiple delays, Math. Comput. Simul., 2018, 149, 69-90. doi: 10.1016/j.matcom.2018.02.002 [50] C. Xu, Periodic solution of competition and corporation dynamical model of two enterprises on time scales, J. Quant. Econ., 2012, 29(2), 1-4. [51] C. Xu, M. Liao, Bifurcation analysis of an autonomous epidemic predator-prey model with delay, Ann. Mat. Pur. Appl., 2014, 193(1), 23-28. doi: 10.1007/s10231-012-0264-z [52] C. Xu, Z. Liu, M. Liao, P. Li, Q. Xiao, S. Yuan, Fractional-order bidirectional associate memory (BAM) neural networks with multiple delays: The case of Hopf bifurcation, Math. Comput. Simul., 2021, 182, 471-494. doi: 10.1016/j.matcom.2020.11.023 [53] C. Xu, Y. Shao, Existence and global attractivity of periodic solution for enterprise clusters based on ecology theory with impulse, J. Appl. Math. Comput., 2012, 39(1-2), 367-384. doi: 10.1007/s12190-011-0530-z [54] C. Xu, X. Tang, M. Liao, Frequency domain analysis for bifurcation in a simplified tri-neuron BAM network model with two delays, Neural Netw., 2010, 23(7), 872-880. doi: 10.1016/j.neunet.2010.03.004 [55] C. Xu, X. Tang, M. Liao, Stability and bifurcation analysis of a delayed predator-prey model of prey dispersal in two-patch environments, Appl. Math. Comput., 2010, 216(10), 2920-2936. [56] C. Xu, X. Tang, M. Liao, Stability and bifurcation analysis of a six-neuron BAM neural network model with discrete delays, Neurocomput., 2011, 74(5), 689-707. doi: 10.1016/j.neucom.2010.09.002 [57] C. Xu, Y. Wu, Bifurcation and control of chaos in a chemical system, Appl. Math. Modelling, 2015, 39(8), 2295-2310. doi: 10.1016/j.apm.2014.10.030 [58] C. Xu, Q. Zhang, Bifurcation analysis of a tri-neuron neural network model in the frequency domain, Nonlinear Dyna., 2014, 76(1), 33-46. doi: 10.1007/s11071-013-1107-1 [59] X. Yang, C. Li, Q. Song, J. Chen, J. Huang, Global Mittag-Leffler stability and synchronization analysis of fractional-order quaternion-valued neural networks with linear threshold neurons, Neural Netw., 2018, 105, 88-103. doi: 10.1016/j.neunet.2018.04.015 [60] X. Zhang, L. Liu, Y. Wu, B. Wiwatanapataphee, Nontrivial solutions for a fractional advection dispersion equation in anomalous diffusion, Appl. Math. Lett., 2017, 66, 1-8. doi: 10.1016/j.aml.2016.10.015 [61] Y. Zhi, Z. Ding, Y. Li, Permanence and almost periodic solution for an enterprise cluster model based on ecology theory with feedback controls on time scales, Discrete Dyn. Nat. Soc., Volume 2013, Article ID 639138, 14 pages. [62] B. Zhu, L. Liu, Y. Wu, Existence and uniqueness of global mild solutions for a class of nonlinear fractional reaction-diffusion equations with delay, Comput. Math. Appl., 2019, 78(6), 1811-1818. doi: 10.1016/j.camwa.2016.01.028 [63] F. Zouari, A. Ibeas, A. Boulkroune, J. Cao, M. M. Arefi, Adaptive neural output-feedback control for nonstrict-feedback time-delay fractional-order systems with output constraints and actuator nonlinearities, Neural Netw., 2018, 105, 256-276. doi: 10.1016/j.neunet.2018.05.014 [64] M. Zuo, X. Hao, L. Liu, Y. Cui, , Existence results for impulsive fractional integro-differential equation of mixed type with constant coefficient and antiperiodic boundary conditions, Bound. Value Probl., 2017, 161, 1-15. -
-
Figures(16) / Tables(2)
Export File
Citation
Changjin Xu, Maoxin Liao, Peiluan Li, Shuai Yuan. NEW INSIGHTS ON BIFURCATION IN A FRACTIONAL-ORDER DELAYED COMPETITION AND COOPERATION MODEL OF TWO ENTERPRISES[J]. Journal of Applied Analysis & Computation, 2021, 11(3): 1240-1258. doi: 10.11948/20200087
Format
Content
DownLoad:
-
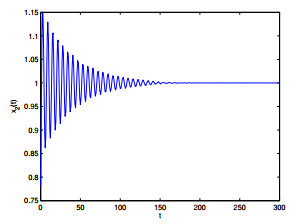
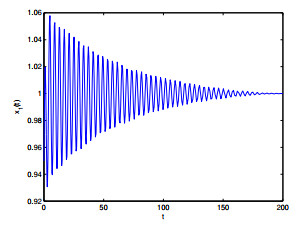
Figure 1. The relation of
$ t $ -$ x_1(t) $ when$ \varepsilon_1 = 0, \varepsilon_2 = 1.8<\varepsilon_{20} = 1.9939. $ -
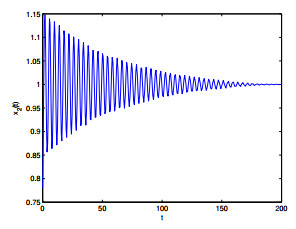
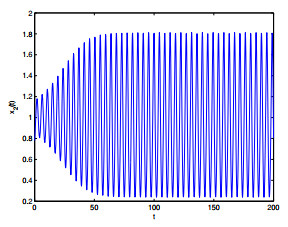
Figure 2. The relation of
$ t $ -$ x_2(t) $ when$ \varepsilon_1 = 0, \varepsilon_2 = 1.8<\varepsilon_{20} = 1.9939. $ -
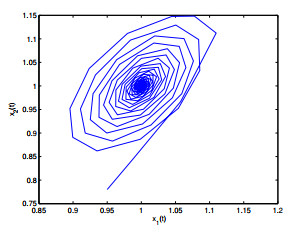
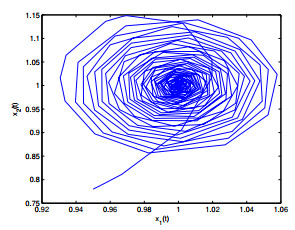
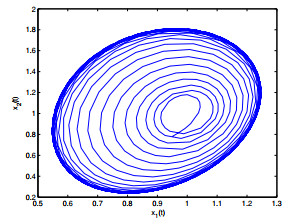
Figure 3. The relation of
$ x_1(t) $ -$ x_2(t) $ when$ \varepsilon_1 = 0, \varepsilon_2 = 1.8 <\varepsilon_{20} = 1.9939. $ -
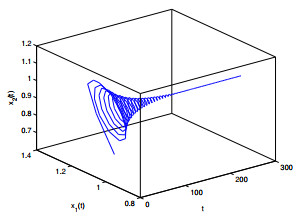
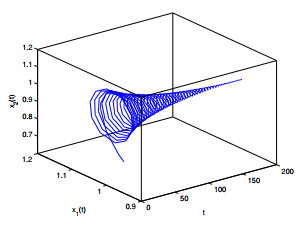
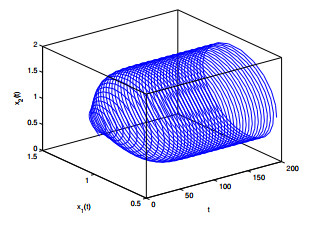
Figure 4. The relation of
$ t $ -$ x_1(t) $ -$ x_2(t) $ when$ \varepsilon_1 = 0, \varepsilon_2 = 1.8 <\varepsilon_{20} = 1.9939. $ -
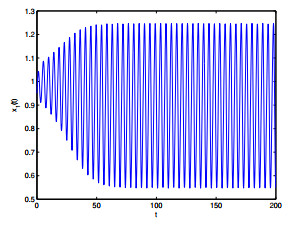
Figure 5. The relation of
$ t $ -$ x_1(t) $ when$ \varepsilon_1 = 0, \varepsilon_2 = 2.2>\varepsilon_{20} = 1.9939. $ -
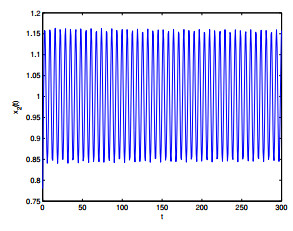
Figure 6. The relation of
$ t $ -$ x_2(t) $ when$ \varepsilon_1 = 0, \varepsilon_2 = 2.2>\varepsilon_{20} = 1.9939. $ -
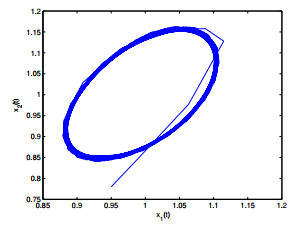
Figure 7. The relation of
$ x_1(t) $ -$ x_2(t) $ when$ \varepsilon_1 = 0, \varepsilon_2 = 2.2 >\varepsilon_{20} = 1.9939. $ -
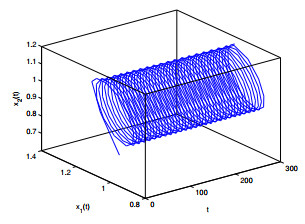
Figure 8. The relation of
$ t $ -$ x_1(t) $ -$ x_2(t) $ when$ \varepsilon_1 = 0, \varepsilon_2 = 2.2 >\varepsilon_{20} = 1.9939. $ -
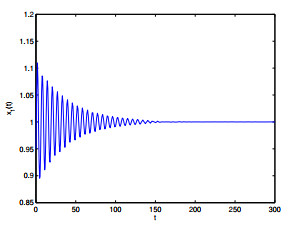
Figure 9. The relation of
$ t $ -$ x_1(t) $ when$ \varepsilon_2 = 1, \varepsilon_1 = 1.0<\varepsilon_{10} = 1.1530. $ -
Figure 10. The relation of
$ t $ -$ x_2(t) $ when$ \varepsilon_2 = 1, \varepsilon_1 = 1.0<\varepsilon_{10} = 1.1530. $ -
Figure 11. The relation of
$ x_1(t) $ -$ x_2(t) $ when$ \varepsilon_2 = 1, \varepsilon_1 = 1.0<\varepsilon_{10} = 1.1530. $ -
Figure 12. The relation of
$ t $ -$ x_1(t) $ -$ x_2(t) $ when$ \varepsilon_2 = 1, \varepsilon_1 = 1.0<\varepsilon_{10} = 1.1530. $ -
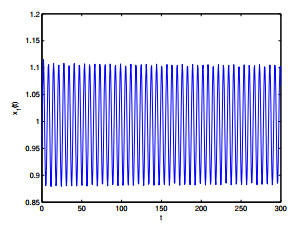
Figure 13. The relation of
$ t $ -$ x_1(t) $ when$ \varepsilon_2 = 1, \varepsilon_1 = 1.2>\varepsilon_{10} = 1.1530. $ -
Figure 14. The relation of
$ t $ -$ x_2(t) $ when$ \varepsilon_2 = 1, \varepsilon_1 = 1.2>\varepsilon_{10} = 1.1530. $ -
Figure 15. The relation of
$ x_1(t) $ -$ x_2(t) $ when$ \varepsilon_2 = 1, \varepsilon_1 = 1.2>\varepsilon_{10} = 1.1530. $ -
Figure 16. The relation of
$ t $ -$ x_1(t) $ -$ x_2(t) $ when$ \varepsilon_2 = 1, \varepsilon_1 = 1.2>\varepsilon_{10} = 1.1530. $