| Citation: |
Guangjie Li, Qigui Yang. STABILITY ANALYSIS BETWEEN THE HYBRID STOCHASTIC DELAY DIFFERENTIAL EQUATIONS WITH JUMPS AND THE EULER-MARUYAMA METHOD[J]. Journal of Applied Analysis & Computation, 2021, 11(3): 1259-1272. doi: 10.11948/20200127
|
STABILITY ANALYSIS BETWEEN THE HYBRID STOCHASTIC DELAY DIFFERENTIAL EQUATIONS WITH JUMPS AND THE EULER-MARUYAMA METHOD
-
Abstract
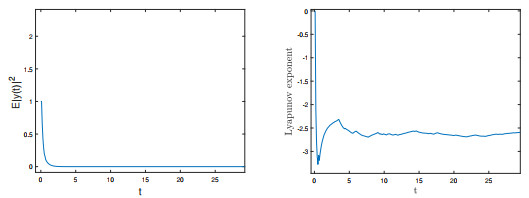
The aim of this paper is to concern with the mean square exponential stability equivalence between the hybrid stochastic delay differential equations with jumps and the Euler-Maruyama method (EM-method). Precisely, under the global Lipschitz condition, it is shown that a stochastic delay differential equation with Markovian switching and jumps (SDDEwMJ) is mean square exponentially stable if and only if for some sufficiently small step size, its EM-method is mean square exponentially stable. Based on such a result, the mean square exponential stability of a SDDEwMJ can be investigated by the careful numerical simulations in practice without resorting to Lyapunov functions. Moreover, a numerical example is provided to confirm the obtained results.
-
-
References
[1] A. Basse-O'Connor, M. S. Nielsen, J. Pedersen and V. Rohde, Stochastic delay differential equations and related autoregressive models, Stochastics, 2020, 92(3), 454-477. doi: 10.1080/17442508.2019.1635601 [2] D. Conte, R. D'Ambrosio and B. Paternoster, On the stability of θ-methods for stochastic Volterra integral equations, Discrete Contin. Dyn. Syst. Ser. B, 2018, 23(7), 2695-2708. [3] S. Deng, C. Fei, W. Fei and X. Mao, Stability equivalence between the stochastic differential delay equations driven by G-Brownian motion and the Euler-Maruyama method, Appl. Math. Lett., 2019, 96, 138-146. doi: 10.1016/j.aml.2019.04.022 [4] C. Fei, W. Fei, X. Mao, M. Shen and L. Yan, Stability analysis of highly nonlinear hybrid multiple-delay stochastic differential equations, J. Appl. Anal. Comput., 2019, 9(3), 1053-1070. [5] T. D. Frank and P. J. Beek, Stationary solutions of linear stochastic delay differential equations: Applications to biological systems, Phys. Rev. E, 2001, 64(2), 021917. doi: 10.1103/PhysRevE.64.021917 [6] M. J. Garrido-Atienza, A. Neuenkirch and B. Schmalfuß, Asymptotical stability of differential equations driven by H\"older continuous paths, J. Dynam. Differential Equations, 2018, 30(1), 359-377. doi: 10.1007/s10884-017-9574-6 [7] F. B. Hanson, Applied Stochastic Processes and Control for Jump-Diffusion, SIAM, Philadelphia, 2007. [8] D. J. Higham, X. Mao and A. M. Stuart, Exponential mean-square stability of numerical solutions to stochastic differential equations, LMS J. Comput. Math., 2003, 6, 297-313. doi: 10.1112/S1461157000000462 [9] D. J. Higham, X. Mao and C. Yuan, Almost sure and moment exponential stability in the numerical simulation of stochastic differential equations, SIAM J. Numer. Anal., 2007, 45(2), 592-609. doi: 10.1137/060658138 [10] D. J. Higham, X. Mao and C. Yuan, Preserving exponential mean-square stability in the simulation of hybrid stochastic differential equations, Numer. Math., 2007, 108(2), 295-325. doi: 10.1007/s00211-007-0113-y [11] Z. Huang, Q. Yang and J. Cao, Stochastic stability and bifurcation analysis on Hopfield neural networks with noise, Expert Syst. Appl., 2011, 38(8), 10437-10445. doi: 10.1016/j.eswa.2011.02.111 [12] R. Li and Z. Chang, Convergence of numerical solution to stochastic delay differential equation with Poisson jump and Markovian switching, Appl. Math. Comput., 2007, 184(2), 451-463. [13] G. Li and Q. Yang, Stability analysis of the split-step theta method for nonlinear regime-switching jump systems, J. Comput. Math., 2021, 39(2), 192-206. doi: 10.4208/jcm.1910-m2019-0078 [14] H. Li and Q. Zhu, The pth moment exponential stability and almost surely exponential stability of stochastic differential delay equations with Poisson jump, J. Math. Anal. Appl., 2019, 471(1-2), 197-210. doi: 10.1016/j.jmaa.2018.10.072 [15] L. Liu, M. Li and F. Deng, Stability equivalence between the neutral delayed stochastic differential equations and the Euler-Maruyama numerical scheme, Appl. Numer. Math., 2018, 127, 370-386. doi: 10.1016/j.apnum.2018.01.016 [16] J. Luo, Comparison principle and stability of Ito stochastic differential delay equations with Poisson jump and Markovian switching, Nonlinear Anal., 64(2006), 253-262. [17] X. Mao, Stichastic Differential Equations and Applications, Horwood, Chichester, UK, 1997. [18] X. Mao, A. Matasov and A.B. Piunovskiy, Stochastic differential delay equations with Markovian switching, Bernoulli, 2000, 6(1), 73-90. doi: 10.2307/3318634 [19] X. Mao, Almost sure exponential stability in the numerical simulation of stochastic differential equations, SIAM J. Numer. Anal., 2015, 53(1), 370-389. doi: 10.1137/140966198 [20] X. Mao and C. Yuan, Stochastic Differential Equations with Markovian Switching, Imperial college press, 2006. [21] M. Mariton, Jump linear systems in automatic control, New York and Basel, 1990, 37-52. [22] M. Milošević, Convergence and almost sure polynomial stability of the backward and forward-backward Euler methods for highly nonlinear pantograph stochastic differential equations, Math. Comput. Simulation, 2018, 150, 25-48. doi: 10.1016/j.matcom.2018.02.006 [23] S. Pang, F. Deng and X. Mao, Almost sure and moment exponential stability of Euler-Maruyama discretizations for hybrid stochastic differential equations, J. Comput. Appl. Math., 2008, 213(1), 127-141. doi: 10.1016/j.cam.2007.01.003 [24] A. Rathinasamy and J. Narayanasamy, Mean square stability and almost sure exponential stability of two step Maruyama methods of stochastic delay Hopfield neural networks, Appl. Math. Comput., 2019, 348, 126-152. [25] L. Shaikhet, About stability of delay differential equations with square integrable level of stochastic perturbations, Appl. Math. Lett., 2019, 90, 30-35. doi: 10.1016/j.aml.2018.10.004 [26] Y. Shen, Q. Meng and P. Shi, Maximum principle for mean-field jump-diffusion stochastic delay differential equations and its application to finance, Automatica, 2014, 50(6), 1565-1579. doi: 10.1016/j.automatica.2014.03.021 [27] A. V. Svishchuk and YuI. Kazmerchuk, Stability of stochastic delay equations of Ito form with jumps and Markovian switchings, and their applications in finance, Theor. Probab. Math. Stat., 2002, 64, 167-178. [28] T. Tian, K. Burrage, P. M. Burrage and M. Carletti, Stochastic delay differential equations for genetic regulatory networks, J. Comput. Appl. Math., 2007, 205(2), 696-707. doi: 10.1016/j.cam.2006.02.063 [29] L. Wang and H. Xue, Convergence of numerical solutions to stochastic differential delay equations with Poisson jump and Markovian switching, Appl. Math. Comput., 2007, 188(2), 1161-1172. [30] Q. Yang and G. Li, Exponential stability of θ-method for stochastic differential equations in the G-framework, J. Comput. Appl. Math., 2019, 350, 195-211. doi: 10.1016/j.cam.2018.10.020 [31] C. Zeng, Y. Chen and Q. Yang, Almost sure and moment stability properties of fractional order Black-Scholes model, Fract. Calc. Appl. Anal., 2013, 16(2), 317-331. [32] W. Zhang, J. Ye and H. Li, Stability with general decay rates of stochastic differential delay equations with Poisson jumps and Markovian switching, Statist Probab. Lett., 2014, 92, 1-11. doi: 10.1016/j.spl.2014.04.024 [33] X. Zhao and F. Deng, A new type of stability theorem for stochastic systems with application to stochastic stabilization, IEEE Trans. Automat. Control, 2016, 61(1), 240-245. doi: 10.1109/TAC.2015.2438414 -
-
Figures(2)
Export File
Citation
Guangjie Li, Qigui Yang. STABILITY ANALYSIS BETWEEN THE HYBRID STOCHASTIC DELAY DIFFERENTIAL EQUATIONS WITH JUMPS AND THE EULER-MARUYAMA METHOD[J]. Journal of Applied Analysis & Computation, 2021, 11(3): 1259-1272. doi: 10.11948/20200127
Format
Content
DownLoad:
-
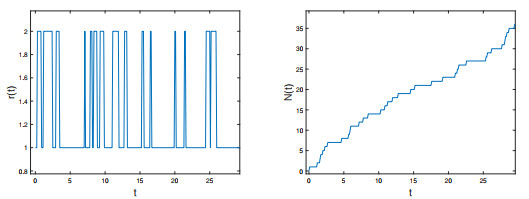
Figure 1. The numerical simulation of the
$ r(t) $ (left) and the$ N(t) $ (right). - Figure 2. The mean square curves of numerical solution (left) and the Lyapunov exponent (right) of Eq. (4.1).