| Citation: | Jacobo Baldonedo, José R. Fernández. AN A PRIORI ERROR ANALYSIS OF A STRAIN GRADIENT MODEL USING C0 INTERIOR PENALTY METHODS[J]. Journal of Applied Analysis & Computation, 2021, 11(5): 2303-2312. doi: 10.11948/20200374 |
AN A PRIORI ERROR ANALYSIS OF A STRAIN GRADIENT MODEL USING C0 INTERIOR PENALTY METHODS
-
Abstract
In this work we study, from the numerical point of view, a strain gradient model. It can be written as a linear fourth-order in space and second-order in time partial differential equation which leads to a parabolic variational equation in terms of the velocity field. Then, a fully discrete approximation is provided by using the implicit Euler scheme to discretize the time derivatives and the so-called $ C^0 $ interior penalty method for the spatial approximation. A priori error estimates are obtained, and from them it follows the convergence of the approximations (under suitable regularity conditions). Finally, some two-dimensional numerical simulations are shown to demonstrate the numerical behaviour.
-

-
References
[1] G. Ahmadi and K. Firoozbaksh, First strain-gradient theory of thermoelasticity, Internat. J Solids Struct., 1975, 11(3), 339-345. doi: 10.1016/0020-7683(75)90073-6 [2] J. Ahn, S. Lee and E. J. Park, Computation C0 interior penalty methods for a dynamic nonlinear beam model, Appl. Math. Comp., 2018, 339, 685-700. doi: 10.1016/j.amc.2018.07.043 [3] A. Beheshti, A numerical analysis of saint-venant torsion in strain-gradient bars, Eur. J. Mech. A., 2018, 70, 181-190. doi: 10.1016/j.euromechsol.2018.02.001 [4] S. C. Brenner and L. Y. Sung, C0 Interior Penalty Methods for Fourth Order Elliptic Boundary Value Problems on Polygonal Domains, J. Sci. Computing., 2005, 22-23, 83-118. doi: 10.1007/s10915-004-4135-7 [5] M. Campo, J. R. Fernández, K. L. Kuttler, M. Shillor and J. M. Viaño, Numerical analysis and simulations of a dynamic frictionless contact problem with damage, Comput. Methods Appl. Mech. Engrg., 2006, 196(1-3), 476-488. doi: 10.1016/j.cma.2006.05.006 [6] P. G. Ciarlet, Basic error estimates for elliptic problems. In: Handbook of Numerical Analysis, P. G. Ciarlet and J. L. Lions eds., 1993, 2, 17-351. [7] M. Ciarletta and D. Ieşan, Non-classical elastic solids, Longman Scientific & Technical, London, 1993. [8] S. Chowdhury and T. Gudi, C0 interior penalty method for the Dirichlet control problem governed by biharmonic operator, J. Comput. Appl. Math., 2017, 317, 290-306. doi: 10.1016/j.cam.2016.12.005 [9] J. R. Fernández, A. Magaña, M. Masid and R. Quintanilla, Analysis for the strain gradient theory of porous thermoelasticity, J. Comput. Appl. Math., 2019, 345, 247-268. doi: 10.1016/j.cam.2018.06.045 [10] H. Fernández-Sare, J. Muñoz Rivera and R. Quintanilla, Decay of solutions in nonsimple thermoelastic bars, Internat. J. Engrg. Sci., 2010, 48, 1233-1241. doi: 10.1016/j.ijengsci.2010.04.014 [11] S. Forest, R. Sievert and E. C. Aifantis, Strain gradient crystal plasticity: Thermomechanical formulations and applications, J. Mech. Behav. Mat., 2002, 13, 219-232. doi: 10.1515/JMBM.2002.13.3-4.219 [12] T. Gudi and K. Porwal, A C0 interior penalty method for a fourth-order variational inequality of the second kind, Numer. Methods Partial Diff. Equations., 2016, 32, 36-59. doi: 10.1002/num.21983 [13] F. Hecht, New development in FreeFem++, J. Numer. Math., 2012, 20, 251-265. [14] D. Ieşan, Thermoelastic Models of Continua, Solid Mechanics and its Applications, Springer, Dordrecht, 2004, 118. [15] D. Ieşan and R. Quintanilla, Some theorems in the theory of nonsimple elastic bodies, An. Şt. Univ. Iasi, Matematica., 1991, 37, 113-124. [16] D. Ieşan and R. Quintanilla, On the grade consistent theory of micropolar thermoelasticity, J. Thermal Stresses., 1992, 15, 393-418. doi: 10.1080/01495739208946146 [17] D. Ieşan and R. Quintanilla, Qualitative properties in strain gradient thermoelasticity with microtemperatures, Math. Mech. Solids., 2018, 23, 240-258. doi: 10.1177/1081286516680860 [18] Z. Liu, A. Magaña and R. Quintanilla, On the time decay of solutions for non-simple elasticity with voids, ZAMM., 2016, 96, 857-873. doi: 10.1002/zamm.201400290 [19] A. Logg, K. A. Mardal and G. N. Wells, Automated Solution of Differential Equations by the Finite Element Method, Springer-Verlag GmbH., 2012. [20] R. D. Mindlin, Micro-structure in linear elasticity, Arch. Ration. Mech. Anal., 1964, 16, 51-78. doi: 10.1007/BF00248490 [21] R. A. Toupin, Elastic materials with couple stresses, Arch. Ration. Mech. Anal., 1962, 11, 385-414. doi: 10.1007/BF00253945 -
-
-
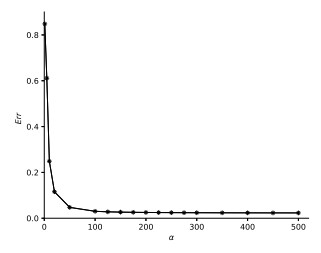
Figure 1. Evolution of the error with respect to parameter
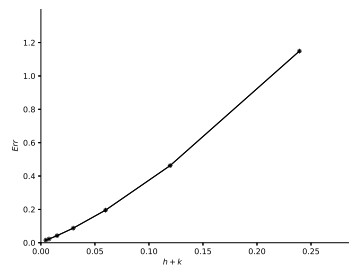
$ \alpha $ . - Figure 2. Numerical convergence of the approximation.
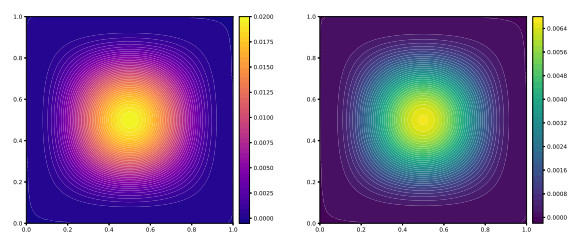
- Figure 3. First components of the velocity (left) and displacement (right) fields.




 DownLoad:
DownLoad: