| Citation: | Feiting Fan, Yuqian Zhou, Xingwu Chen. TRAVELING WAVES AND THEIR EVOLUTION FOR THE ZK(N, 2N, -N) EQUATION[J]. Journal of Applied Analysis & Computation, 2021, 11(6): 2959-2980. doi: 10.11948/20210074 |
TRAVELING WAVES AND THEIR EVOLUTION FOR THE ZK(N, 2N, -N) EQUATION
-
Abstract
In this paper, using the approach of dynamical systems we investigate the traveling waves for the ZK(n, 2n, -n) equation including the types and evolution of traveling waves. The traveling wave problem is converted into the analysis of phase portraits of the corresponding traveling wave system, which is 5-parametric and has a singular line in its phase space. The orbits passing through this singular line in phase portraits are determined by a time rescaling. After converting the orbits in these phase portraits into traveling waves, we state all types of traveling waves and give at least one exact traveling wave solution for each type of bounded traveling waves in our main results. Finally, we discuss the evolution of these traveling waves among themselves when parameters vary by the bifurcations happening in the phase portraits of the traveling wave system.
-
Keywords:
- Compacton /
- solitary wave /
- solitary cusp wave /
- traveling wave /
- ZK(n, 2n, -n) equation
-

-
References
[1] A. Biswas, 1-soliton solution of the generalized zakharov-kuznetsov equation with nonlinear dispersion and time-dependent coefficients, Physics Letters A, 2009, 373(33), 2931-2934. doi: 10.1016/j.physleta.2009.06.029 [2] A. Biswas and E. Zerrad, Solitary wave solution of the zakharov-kuznetsov equation in plasmas with power law nonlinearity, Nonlinear Anal. : Real World Appl., 2010, 11(4), 3272-3274. doi: 10.1016/j.nonrwa.2009.08.007 [3] C. Deng, New exact solutions to the zakharov-kuznetsov equation and its generalized form, Comm. Nonlinear Sci. Num. Simul., 2010, 15(4), 857-868. doi: 10.1016/j.cnsns.2009.05.011 [4] Z. Du, Z. Feng and X. Zhang, Traveling wave phenomena of n-dimensional diffusive predator-prey systems, Nonlinear Anal. : Real World Appl., 2018, 41, 288-312. doi: 10.1016/j.nonrwa.2017.10.012 [5] Y. Fu and J. Li, Bifurcations of travelling wave solutions in three modified Camassa-Holm equations, J. Appl. Anal. Comput., 2021, 11(2), 1051-1061. [6] A. Johnpillai, A. Kara and A. Biswas, Symmetry solutions and reductions of a class of generalized (2+1)-dimensional zakharov-kuznetsov equation, Int. J. Nonlinear Sci. Num. Simul., 2011, 12(1-8), 45-50. doi: 10.1515/ijnsns.2011.003 [7] T. Kano and T. Nishida, A mathematical justification for korteweg-de vries equation and boussinesq equation of water surface waves, Osaka J. Math., 1986, 23(2), 389-413. [8] D. Korteweg and G. de Vries, On the change of form of long waves advancing in a rectangular canal, and on a new type of long stationary waves, Philosophical Magazine, 1895, 39(240), 422-443. [9] S. Lai, J. Yin and Y. Wu, Different physical structures of solutions for two related zakharov-kuznetsov equations, Physics Letters A, 2008, 372(43), 6461-6468. doi: 10.1016/j.physleta.2008.08.071 [10] J. Li, Geometric properties and exact travelling wave solutions for the generalized Burger-Fisher equation and the Sharma-Tasso-Olver equation, J. Nonlinear Model. Anal., 2019, 1(1), 1-10. [11] J. Li and G. Chen, On a class of singular nonlinear traveling wave equations, Int. J. Bifurcation and Chaos, 2007, 17(11), 4049-4065. doi: 10.1142/S0218127407019858 [12] B. Li, Y. Chen and H. Zhang, Exact traveling wave solutions for a generalized zakharov-kuznetsov equation, Appl. Math. Comput., 2003, 146(2-3), 653-666. [13] J. Li, J. Wu and H. Zhu, Traveling waves for an integrable higher order kdv type wave equations, Int. J. Bifurcation and Chaos, 2006, 16(08), 2235-2260. doi: 10.1142/S0218127406016033 [14] J. Li, Y. Zhang and J. Liang, Bifurcations and exact traveling wave solutions for a new integrable nonlocal equation, J. Appl. Anal. Comput., 2021, 11(3), 1588-1599. [15] A. Ludu and J. Draayer, Patterns on liquid surfaces: cnoidal waves, compactons and scaling, Physica D: Nonlinear Phen., 1998, 123(1-4), 82-91. doi: 10.1016/S0167-2789(98)00113-4 [16] P. Meuris and F. Verheest, Korteweg-de vries equation for magnetosonic modes in dusty plasmas, Physics Letters A, 1996, 219(5-6), 299-302. doi: 10.1016/0375-9601(96)00473-2 [17] S. Munro and E. Parkes, The derivation of a modified zakharov-kuznetsov equation and the stability of its solutions, J. Plasma Physics, 1999, 62(3), 305-317. doi: 10.1017/S0022377899007874 [18] P. Rosenau, Nonlinear dispersion and compact structures, Phys. Rev. Lett., 1994, 73(13), 1737-1741. doi: 10.1103/PhysRevLett.73.1737 [19] P. Rosenau and J. Hyman, Compactons: solitons with finite wavelength, Phys. Rev. Lett., 1993, 70(5), 564-567. doi: 10.1103/PhysRevLett.70.564 [20] F. Tappert and C. Varma, Asymptotic theory of self-trapping of heat pulses in solids, Phys. Rev. Lett., 1970, 25(16), 1108-1111. doi: 10.1103/PhysRevLett.25.1108 [21] A. Wazwaz, Compactons and solitary patterns structures for variants of the KdV and the KP equations, Appl. Math. Comput., 2003, 139(1), 37-54. [22] A. Wazwaz, An analytic study of Compactons structures in a class of nonlinear dispersive equations, Math. Comput. Simul., 2003, 63(1), 35-44. doi: 10.1016/S0378-4754(02)00255-0 [23] A. Wazwaz, Special types of the nonlinear dispersive zakharov-kuznetsov equation with compactons, solitons, and periodic solutions, Int. J. Comp. Math., 2004, 81(9), 1107-1119. doi: 10.1080/00207160410001684253 [24] A. Wazwaz, Exact solutions with solitons and periodic structures for the zakharov-kuznetsov (zk) equation and its modified form, Comm. Nonlinear Sci. Num. Simul., 2005, 10(6), 597-606. doi: 10.1016/j.cnsns.2004.03.001 [25] A. Wazwaz, Explicit traveling wave solutions of variants of the k(n, n) and the zk(n, n) equations with compact and noncompact structures, Appl. Math. Comput., 2006, 173(1), 213-230. [26] A. Wazwaz, The extended tanh method for the zakharov-kuznetsov (zk) equation, the modified zk equation, and its generalized forms, Comm. Nonlinear Sci. Num. Simul., 2008, 13(6), 1039-1047. doi: 10.1016/j.cnsns.2006.10.007 [27] M. Wei and S. Yang, Periodic traveling wave solutions of zk(2, 4, -2) equation, J. Advances in Math. Comp. Sci., 2014, 4(13), 1849-1856. [28] S. Wu and G. Chen, Uniqueness and exponential stability of traveling wave fronts for a multi-type SIS nonlocal epidemic model, Nonlinear Anal. : Real World Appl., 2017, 36, 267-277. doi: 10.1016/j.nonrwa.2017.02.001 [29] B. Xia, Z. Qiao and J. Li, An integrable system with peakon, complex peakon, weak kink, and kink-peakon interactional solutions, Comm. Nonlinear Sci. Num. Simul., 2018, 63, 292-306. doi: 10.1016/j.cnsns.2018.03.019 [30] E. Yomba, Jacobi elliptic function solutions of the generalized zakharov-kuznetsov equation with nonlinear dispersion and t-dependent coefficients, Physics Letters A, 2010, 374(15-16), 1611-1615. doi: 10.1016/j.physleta.2010.02.026 [31] N. Zabusky and M. Kruskal, Interaction of solitons in a collisionless plasma and the recurrence of initial states, Phys. Rev. Lett., 1965, 15(6), 240-243. doi: 10.1103/PhysRevLett.15.240 [32] V. Zakharov and E. Kuznetsov, On threedimensional solitons, Zhurnal Eksp. Teoret. Fiz., 1974, 66, 594-597. [33] Z. Zhang, T. Ding, W. Huang and Z. Dong, Qualitative Theory of Differential Equations, Transl. Math. Monogr., Amer. Math. Soc., Providence, RI, 1992. -
-
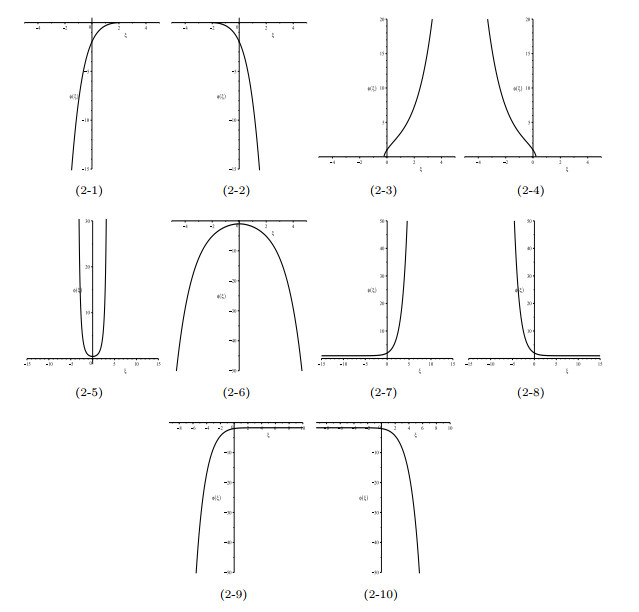
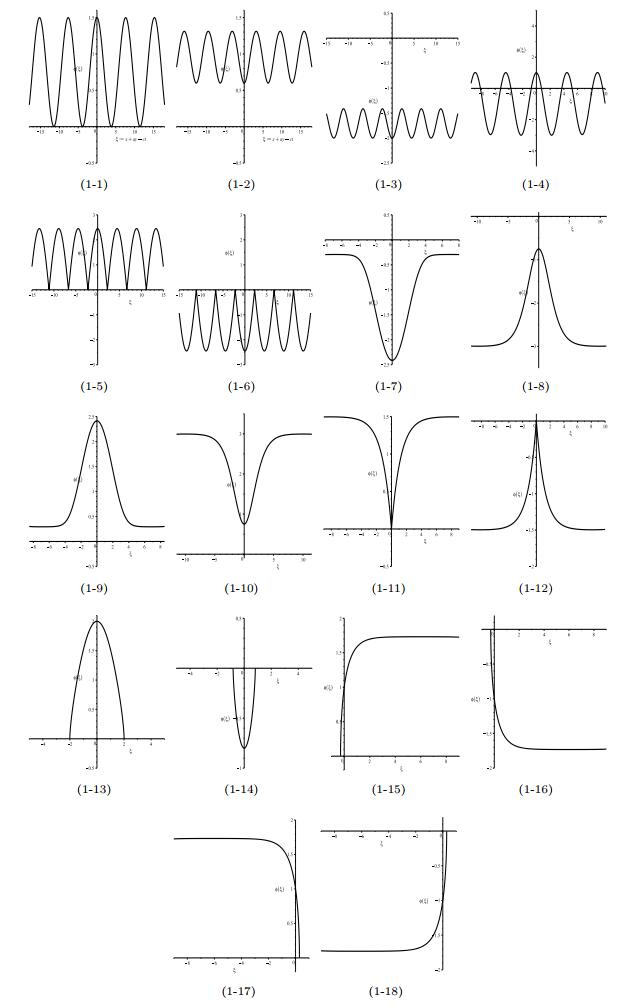
- Figure 1. Graphs of bounded traveling waves for equation (1.4).
- Figure 2. Graphs of unbounded traveling waves for equation (1.4).
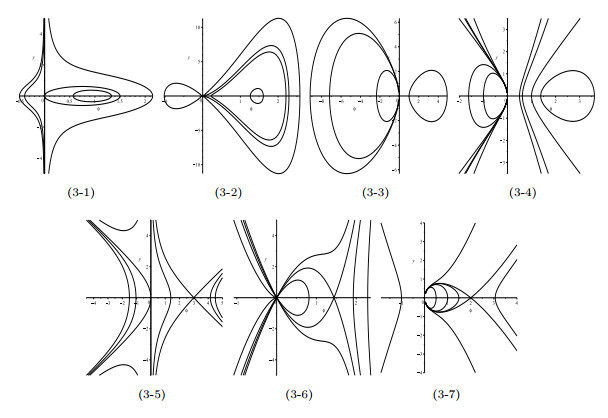
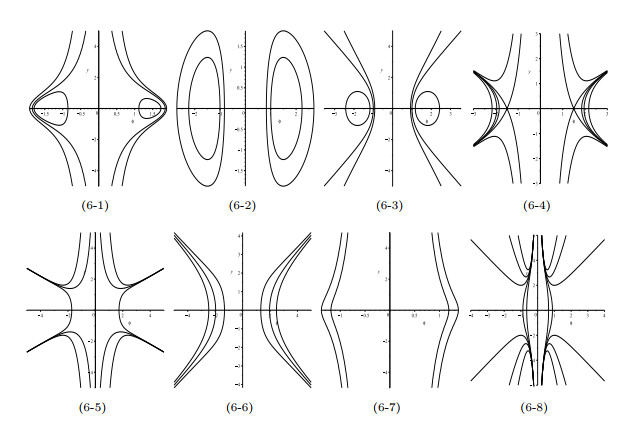
- Figure 3. Phase portraits of system (1.8).
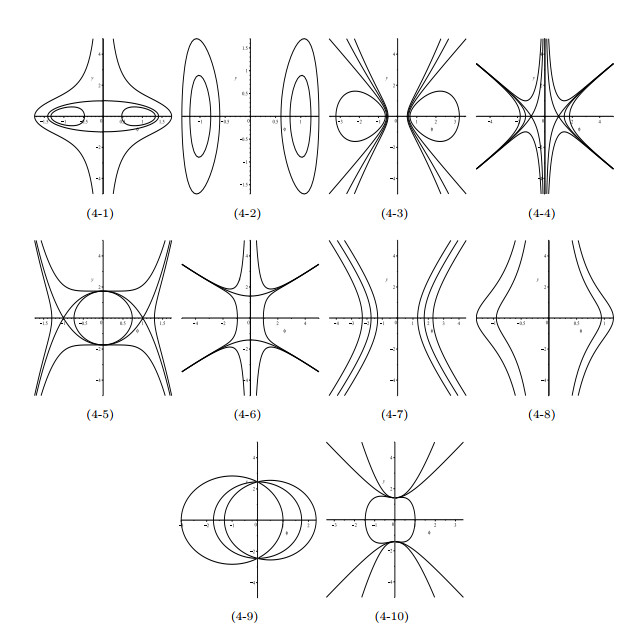
- Figure 4. Phase portraits of system (1.9).
-
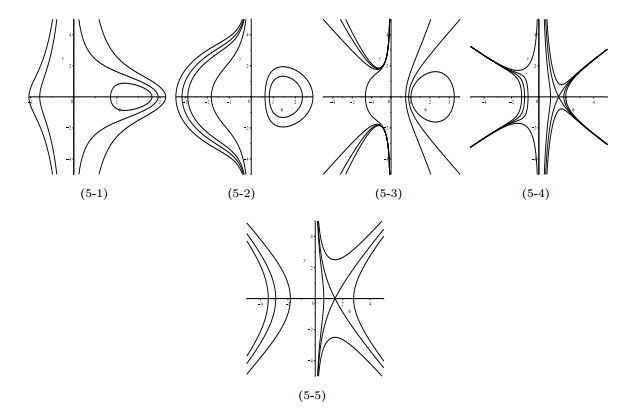
Figure 5. Phase portraits of (1.10) for even
$ n\geqslant4 $ . -
Figure 6. Phase portraits of (1.10) for odd
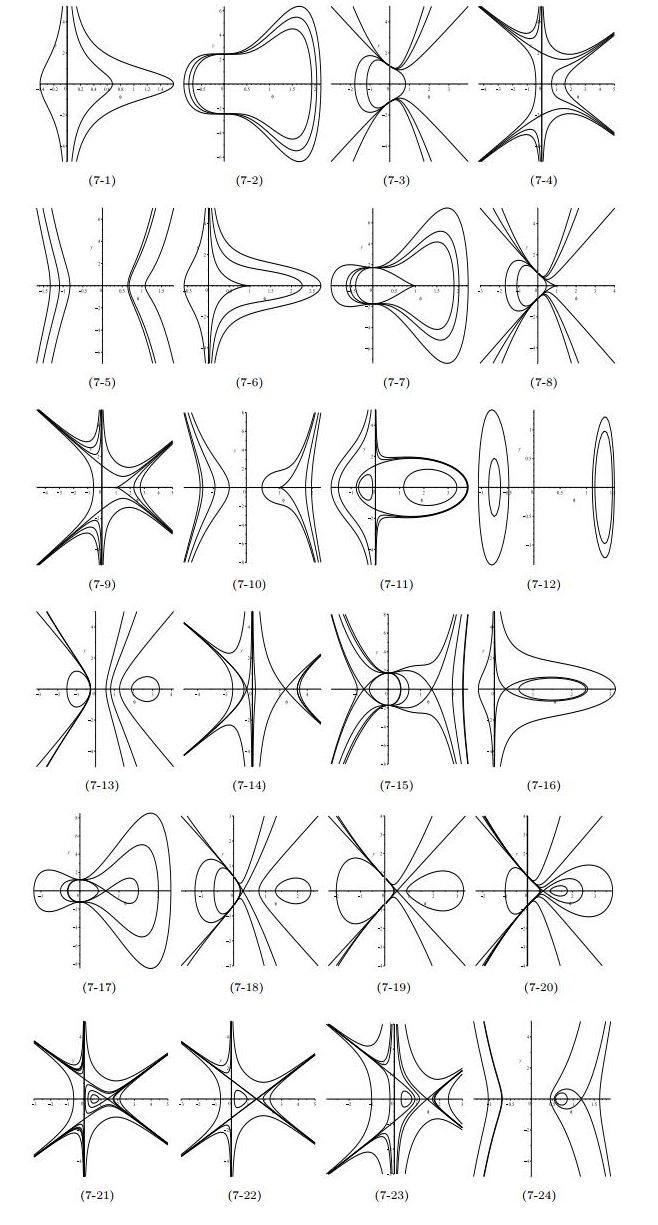
$ n\geqslant5 $ . - Figure 7. Phase portraits of system (1.11).
-
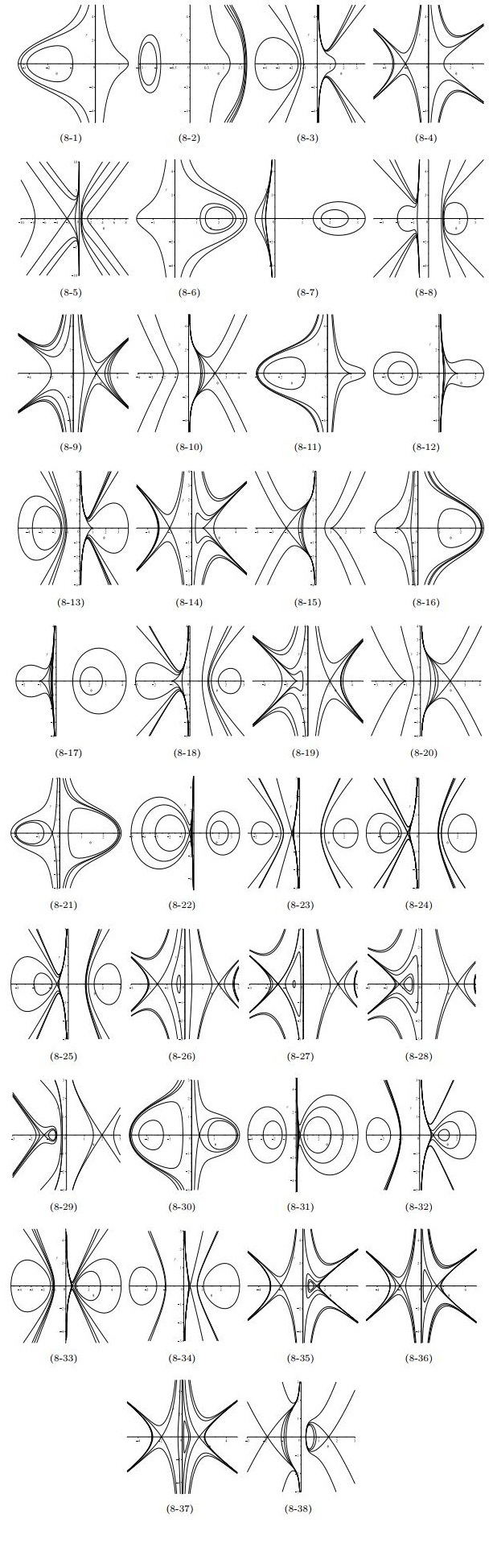
Figure 8. The phase portraits of system (1.12) for
$ n = 2m+1\geqslant3 $ . -
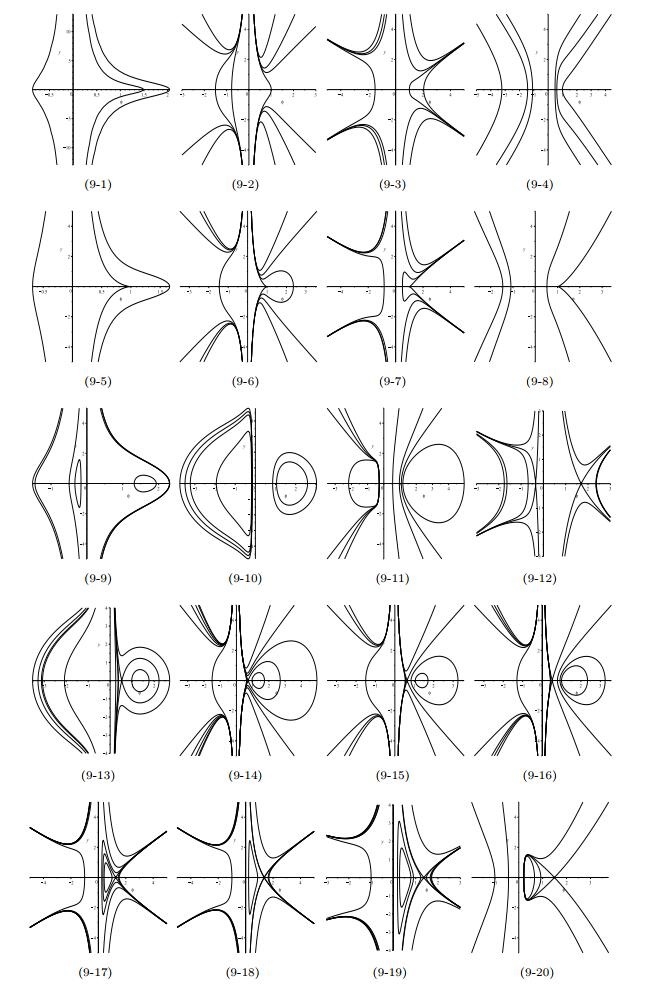
Figure 9. The phase portraits of system (1.12) for
$ n = 2m\geqslant4 $ .




 DownLoad:
DownLoad: