| Citation: |
Huimiao Dong, Tiansi Zhang, Xingbo Liu. BIFURCATIONS OF DOUBLE HETERODIMENSIONAL CYCLES WITH THREE SADDLE POINTS[J]. Journal of Applied Analysis & Computation, 2022, 12(6): 2143-2162. doi: 10.11948/20210082
|
BIFURCATIONS OF DOUBLE HETERODIMENSIONAL CYCLES WITH THREE SADDLE POINTS
-
Abstract
In this paper, bifurcations of double heterodimensional cycles of an "$\infty$" shape consisting of two saddles of (1,2) type and one saddle of (2,1) type are studied in three dimensional vector field. We discuss the gaps between returning points in transverse sections by establishing a local active coordinate system in the tubular neighborhood of unperturbed double heterodimensional cycles, through which the preservation of "$\infty$"-shape double heterodimensional cycles is proved. We then get the existence of a new heteroclinic cycle consisting of two saddles of (1,2) type and one saddle of (2,1) type, which is composed of one big orbit linking $p_1$, $p_3$ and two orbits linking $p_3$, $p_2$ and $p_2$, $p_1$ respectively, and another heterodimensional cycle consisting of one saddle $p_1$ of (2,1) type and one saddle $p_2$ of (1,2) type, which is composed of one orbit starting from $p_1$ to $p_2$ and another orbit starting from $p_2$ to $p_1$. Moreover, the 1-fold and 2-fold large 1-heteroclinic cycle consisting of two saddles $p_1$ and $p_3$ of (1,2) type is also presented. As well as the coexistence of a 1-fold large 1-heteroclinic cycle and the "$\infty$"-shape double heterodimensional cycles and the coexistence conditions are also given in the parameter space.
-
-
References
[1] P. Aguirre, B. Krauskopf and H. M. Osinga, Global invariant manifolds near a Shilnikov homoclinic bifurcation, J. Comput. Dyn., 2014, 1(1), 1–38. doi: 10.3934/jcd.2014.1.1 [2] C. Bonatti and J. D. Lorenzo, Robust heterodimensional cycles and $C^1$-generic dynamics, J. Inst. Math. Jussieu, 2008, 7(3), 469–525. [3] S. N. Chow, B. Deng and B. Fiedler, Homoclinic bifurcation at resonant eigenvalues, J. Dyn. Differ. Equ., 1990, 2(2), 177–244. doi: 10.1007/BF01057418 [4] Z. Du and W. Zhang, Melnikov method for homoclinic bifurcation in nonlinear impact oscillators, Comput. Math. Appl., 2005, 50(3–4), 445–458. doi: 10.1016/j.camwa.2005.03.007 [5] L. J. Díaz, Persistence of cycles and nonhyperbolic dynamics at heteroclinic bifurcations, Nonlinearity, 1995, 8(5), 693–713. doi: 10.1088/0951-7715/8/5/003 [6] F. Geng, Bifurcations of heterodimensional cycles and heteroclinic loop and BVPS of dynamic equations on time scales, East China Normal University, China, 2007. [7] F. Geng and J. Zhao, Bifurcations of orbit and inclination flips heteroclinic loop with nonhyperbolic equilibria, Sci. World J. 2014. DOI: 10.1155/2014/585609. [8] F. Geng, D. Liu and D. Zhu, Bifurcations of generic heteroclinic loop accompanied by transcritical bifurcation, Int. J. Bifurcat. Chaos, 2008, 18(4), 1069–1083. doi: 10.1142/S0218127408020847 [9] F. Geng, X. Lin and X. Liu, Chaotic traveling wave solutions in coupled chua's circuits, J. Dyn. Differ. Equ., 2019, 31, 1373–1396. doi: 10.1007/s10884-017-9631-1 [10] M. Han, D. Luo, X. Wang and D. Zhu, Bifurcation theory and methods of dynamical systems, World Science, Singapore, 1997. [11] M. Han and H. Zhu, The loop quantities and bifurcations of homoclinic loops, J. Dyn. Differ. Equ., 2007, 234(2), 339–359. doi: 10.1016/j.jde.2006.11.009 [12] A. J. Homburg and B. Sandstede, Homoclinic and Heteroclinic Bifurcations in Vector ${\bf R}^3$ Fields, Handbook of dynamical systems, 2010(3), 379–524. [13] A. J. Homburg and B. Krauskopf, Resonant homoclinic flip bifurcation, J. Dyn. Differ. Equ., 2000, 12(4), 807–850. doi: 10.1023/A:1009046621861 [14] G. John and P. Holmes, Nonlinear oscillations, dynamical systems, and bifurcations of vector fields, Springer Science and Business Media, New York, 2013. [15] Y. Jin and D. Zhu, Bifurcations of rough heteroclinic loops with three saddle points, Acta. Math. Sin., 2002, 18(1), 199–208. doi: 10.1007/s101140100139 [16] Y. Jin, X. Zhu, Z. Guo, H. Xu, L. Zhang and B. Ding, Bifurcations of nontwisted heteroclinic loop with resonant eigenvalues, Sci. World J., 2014. DOI: 10.1155/2014/716082. [17] Y. Jin, S. Yang, Y. Liu, D. Xie and N. Zhang, Bifurcations of heteroclinic loop with twisted conditions, Int. J. Bifurcat. Chaos, 2017, 27(08), 1750120. doi: 10.1142/S0218127417501206 [18] Y. Jin, X. Zhu, Y. Liu, H. Xu and N. Zhang, Bifurcations of twisted heteroclinic loop with resonant eigenvalues, Nonlinear Dynam., 2018, 92(2), 557–573. doi: 10.1007/s11071-018-4075-7 [19] Y. Jin, H. Xu, Y. Gao, X. Zhao and D. Xie, Bifurcations of resonant double homoclinic loops for higher dimensional systems, J. Math. Comput. Sci., 2016, 16(1), 165–177. [20] G. Kovacic and S. Wiggins, Orbits homoclinic to resonance with an application to chaos in a model of the forced and damped sine-Gordon equation, Physica D., 1992, 57(1–2), 185–225. doi: 10.1016/0167-2789(92)90092-2 [21] J. S. W. Lamb, M. A. Teixeira and N. W. Kevin, Heteroclinic bifurcations near Hopf-zero bifurcation in reversible vector fields in $R^3$, J. Differ. Equation, 2005, 219(1), 78–115. doi: 10.1016/j.jde.2005.02.019 [22] Z. Liu, K. Zhang and M. Li, Exact traveling wave solutions and bifurcation of a generalized (3+1)-dimensional Time-Fractional Camassa-Holm-Kadomtsev-Petviashvili equation, J. Funct. Spaces, 2020. DOI: 10.1155/2020/4532824. [23] D. Liu, M. Han and W. Zhang, Bifurcations of $2-2-1$ heterodimensional cycles under transversality condition, Int. J. Bifurcat. Chaos, 2012, 22(08), 1250191. doi: 10.1142/S021812741250191X CrossRef $2-2-1$ heterodimensional cycles under transversality condition" target="_blank">Google Scholar
[24] D. Liu, S. Ruan and D. Zhu, Nongeneric bifurcations near heterodimensional cycles with inclination flip in $R^4$, Discret. Con. Dyn-S., 2011, 4(6), 1511–1532. [25] X. Liu, Z. Wang and D. Zhu, Bifurcation of rough heteroclinic loop with orbit flips, Int. J. Bifurcat. Chaos, 2012, 22(11), 1250278. doi: 10.1142/S0218127412502781 [26] X. Liu, X. Wang and T. Wang, Nongeneric bifurcations near a nontransversal heterodimensional cycle, Chinese. Ann. Math. B, 2018, 39, 111–128. doi: 10.1007/s11401-018-1055-7 [27] Q. Lu, Z. Qiao, T. Zhang and D. Zhu, Heterodimensional cycle bifurcation with orbit-flip, Int. J. Bifurcat. Chaos, 2010, 20(2), 491–508. doi: 10.1142/S0218127410025569 [28] Q. Lu, D. Zhu and F. Geng, Weak type heterodimensional cycle bifurcation with orbit-flip, Sci. China. Math., 2011, 54(6), 1175–1196. doi: 10.1007/s11425-011-4167-z [29] K. Manna and M. Banerjee, Stability of Hopf-bifurcating limit cycles in a diffusion-driven prey-predator system with Allee effect and time delay, Math. Biosct. Eng., 2019, 16(4), 2411–2446. doi: 10.3934/mbe.2019121 [30] S. Newhouse and J. Palis, Bifurcations of Morse-Smale dynamical systems, Dynamical systems, Academic, 1973, 303–366. [31] E. Pérez-Chavela, M. Santoprete and C. Tamayo, Bifurcation of relative equilibria for vortices and general homogeneous potentials, Qual. Theor. Dyn. Syst., 2020, 19(1), 1–19. doi: 10.1007/s12346-019-00337-5 [32] J. D. M. Rademacher, Homoclinic orbits near heteroclinic cycles with one equilibrium and one periodic orbit, J. Differ. Equation, 2005, 218(2), 390–443. doi: 10.1016/j.jde.2005.03.016 [33] P. D. P. Salazar, Y. Ilyasov, L. F. C. Alberto, E. C. M. Costa and M. B. Salles, Saddle-Node bifurcations of power systems in the context of variational theory and nonsmooth optimization, IEEE Access, 2020, 8, 110986–110993. doi: 10.1109/ACCESS.2020.3002840 [34] D. Shang and M. Han, Global-bifurcation of a perturbed double-homoclinic loop, Chinese Ann. Math. B, 2006, 27(4), 425–436. doi: 10.1007/s11401-004-0487-4 [35] L. P. Shilnikov, Methods of Qualitative Theory in Nonlinear Dynamics, World Scientific, New Jersey, 1998. [36] S. Tomizawa, Hopf-homoclinic Bifurcations and Heterodimensional Cycles, Tokyo J. Math., 2009, 42(2), 449–469. [37] C. K. Tse, D. Dai and X. Ma, Symbolic analysis of bifurcation in switching power converters: a practical alternative viewpoint of border collision, Int. J. Bifurcat. Chaos, 2005, 15(07), 2263–2270. doi: 10.1142/S0218127405013253 [38] M. Wechselberger, Existence and bifurcation of canards in the case of a folded node, SIAM J. Appl. Dyn. Syst., 2005, 4(1), 101–139. [39] Z. Wang and X. Liu, Bifurcations and exact traveling wave solutions for the KdV-like equation, . Nonlinear Dyn., 2019, 95(1), 465–477. doi: 10.1007/s11071-018-4576-4 [40] T. Xu, S. Ji, M. Mei and J. Yin, Sharp oscillatory traveling waves of structured population dynamics model with degenerate diffusion, J. Differ. Equation, 2020, 269(10), 8882–8917. doi: 10.1016/j.jde.2020.06.029 [41] Y. Xu and D. Zhu, Bifurcations of heterodimensional cycles with one orbit flip and one inclination flip, Nonlinear Dyn., 2010, 60(1), 1–13. [42] T. Zhang and D. Zhu, Homoclinic bifurcation of orbit flip with resonant principal eigenvalues, Acta Math. Sin., 2006, 22(3), 855–864. doi: 10.1007/s10114-005-0581-x [43] T. Zhang and D. Zhu, Bifurcations of homoclinic orbit connecting two nonleading eigendirections, Int. J. Bifurcat. Chaos, 2007, 17(3), 823–836. [44] W. Zhang, Bifurcation of double homoclinic loops in four dimensional systems and problems of periodic solutions in population dynamics, East China Normal University, China, 2007. [45] X. Zhang, Homoclinic, heteroclinic and periodic orbits of singularly perturbed systems, Sci. China. Math., 2019, 62(9), 1687–1704. [46] D. Zhu, Problems in homoclinic bifurcation with higher dimensions, Acta Math. Sin., 1998, 14(3), 341–352. doi: 10.1007/BF02580437 [47] D. Zhu and Z. Xia, Bifurcations of heteroclinic loops, Sci. China. Math., 1998, 41(8), 837–848. doi: 10.1007/BF02871667 [48] A. Zilburg and P. Rosenau, Multi-dimensional compactons and compact vortices, J. Phys. A-Math Theor., 2018, 51(39), 395201. doi: 10.1088/1751-8121/aad874 -
-
Figures(4)
Export File
Citation
Huimiao Dong, Tiansi Zhang, Xingbo Liu. BIFURCATIONS OF DOUBLE HETERODIMENSIONAL CYCLES WITH THREE SADDLE POINTS[J]. Journal of Applied Analysis & Computation, 2022, 12(6): 2143-2162. doi: 10.11948/20210082
Format
Content
DownLoad:
-
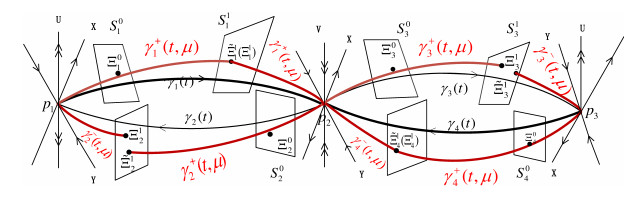
Figure 1. Double heterodimensional cycles of three saddle points
$ p_i $ with four orbits$ \gamma_k(t) $ . -
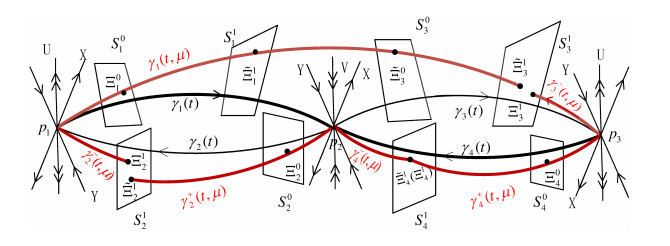
Figure 2. The gap
$ \left\|\gamma_k^+(-T_k+\tilde{T}_k, \mu)-\gamma_k^-(T_k, \mu)\right\|\neq0(k=2, 3) $ in the figure, the original double heterodimensional cycles do not exist. -
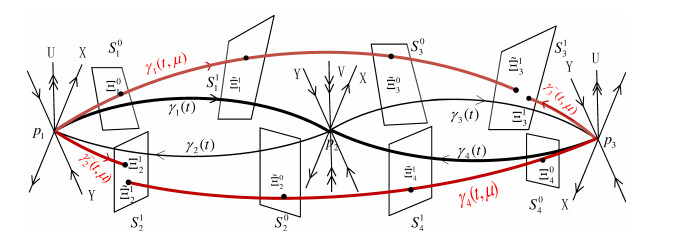
Figure 3. The gap
$ ||{\gamma _1}( - {T_1} + {\tilde T}_1 + {\tau _2} + {\tilde T}_3, \mu ) - \gamma _3^ - ({T_3}, \mu )||\neq0 $ ,$ \left\|\gamma_2^-(T_2, \mu)-\gamma_2^+(-T_2+\tilde T_2, \mu)\right\|\neq0 $ in the figure, there is not the second heterodimensional cycle in general, which consists of two saddles of (1,2) type and one saddle of (2,1) type and is composed of one big orbit linking$ p_1, p_3 $ and two orbits linking$ p_3, p_2 $ and$ p_2, p_1 $ respectively. -
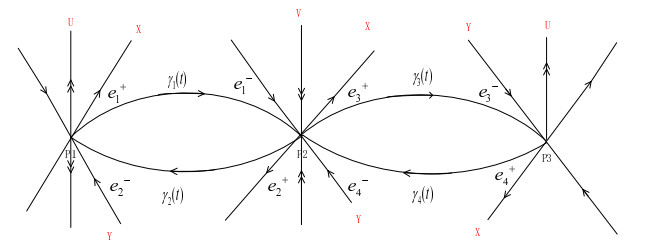
Figure 4. The gap
$ \left\|{\gamma _1}({-T_1} + {\tilde T}_1 + {\tau _2} + {\tilde T}_3, \mu ) - \gamma _3^ - ( {T_3}, \mu )\right\| \neq0 $ ,$ \left\|\gamma_4(-T_4+\tilde T_4+\tau_4+\tilde T_2, \mu)-\right. $ $ \left.\gamma_2^-(T_2, \mu)\right\|\ne 0 $ in the figure, there is not a large 1-heteroclinic cycle in general.