| Citation: | Eduard Musafirov. ADMISSIBLE PERTURBATIONS OF THE THREE-DIMENSIONAL HINDMARSH – ROSE NEURON MODEL[J]. Journal of Applied Analysis & Computation, 2023, 13(4): 1668-1678. doi: 10.11948/20210098 |
ADMISSIBLE PERTURBATIONS OF THE THREE-DIMENSIONAL HINDMARSH – ROSE NEURON MODEL
-
Abstract
For the autonomous Hindmarsh – Rose system the set of admissibly perturbed nonautonomous systems have been obtained. Reflecting functions of the Hindmarsh – Rose system and admissibly perturbed system are coinciding. This allows to investigate the admissibly perturbed systems using outcomes of researches of the well-known Hindmarsh – Rose system and the theory of reflecting function. The results are illustrated by numerical examples.
-

-
References
[1] R. Barrio, S. Ibáñez, L. Pérez and S. Serrano, Spike-adding structure in fold/hom bursters, Commun. Nonlinear Sci. Numer. Simul., 2020, 83, 105100–1–15. [2] I. Bashkirtseva, S. Fedotov, L. Ryashko and E. Slepukhina, Stochastic bifurcations and noise-induced chaos in 3d neuron model, Int. J. Bifurcation and Chaos, 2016, 26(12), 1630032–1–21. [3] M. S. Belokurskii and A. K. Demenchuk, Periodic reflecting function of a nonlinear quasiperiodic differential system with a two-frequency basis, Diff. Eqs., 2013, 49(10), 1323–1327. [4] V. A. Bel'skii, On quadratic differential systems with equal reflecting functions, Diff. Eqs., 2013, 49(12), 1639–1644. [5] D. Chen, W. Zhao, X. Ma and R. Zhang, No-chattering sliding mode control chaos in Hindmarsh–Rose neurons with uncertain parameters, Comput. Math. Appl., 2011, 61(10), 3161–3171. [6] J. M. Gonzàlez-Miranda, Complex bifurcation structures in the Hindmarsh–Rose neuron model, Int. J. Bifurcation and Chaos, 2007, 17(09), 3071–3083. [7] J. L. Hindmarsh and R. M. Rose, A model of neuronal bursting using three coupled first order differential equations, Proc. R. Soc. Lond. B, 1984, 221(1222), 87–102. [8] M. A. Krasnosel'skiĭ, The Operator of Translation Along the Trajectories of Differential Equations, American Mathematical Society, Providence, 2007. [9] W. Liu, Y. Pan and Z. Zhou, The research of periodic solutions of time-varying differential models, Int. J. Differ. Equ., 2014, 2014, 430951–1–6. [10] S. V. Maiorovskaya, Quadratic systems with a linear reflecting function, Diff. Eqs., 2009, 45(2), 271–273. [11] S. A. Malik and A. H. Mir, Synchronization of Hindmarsh Rose neurons, Neural Netw., 2020, 123, 372–380. [12] V. I. Mironenko, Reflective Function and Periodic Solution of the Differential System, University Press, Minsk, 1986 (in Russian). [13] V. I. Mironenko, Reflecting Function and Investigation of Multivariate Differential Systems, Gomel University Press, Gomel, 2004 (in Russian). [14] V. I. Mironenko and V. V. Mironenko, How to construct equivalent differential systems, Appl. Math. Lett., 2009, 22(9), 1356–1359. [15] E. Musafirov, Non-autonomously perturbed autonomous systems of ordinary differential equations, Dynam. Cont. Dis. Ser. B, 2022, 29(6), 447–454. [16] E. Musafirov, A. Grin and A. Pranevich, Admissible perturbations of a generalized Langford system, Int. J. Bifurcation and Chaos, 2022, 32(03), 2250038. [17] E. V. Musafirov, Simplicity of linear differential systems, Diff. Eqs., 2002, 38(4), 605–607. [18] E. V. Musafirov, The reflecting function and the small parameter method, Appl. Math. Lett., 2008, 21(10), 1064–1068. [19] E. V. Musafirov, Perturbations of the Lanford system which do not change the reflecting function, Int. J. Bifurcation and Chaos, 2017, 27(10), 1750154–1–5. [20] E. V. Musafirov, Admissible perturbations of the Hindmarsh–Rose neuron model, Proc. Conf. Innovations in Technology and Education, Kuzbass State Technical University, Belovo, 2019, 317–318 (in Russian). [21] E. V. Musafirov, Admissible perturbations of the Lorenz-84 climate model, Int. J. Bifurcation and Chaos, 2019, 29(06), 1950080–1–8. [22] S. Nikolov, An alternative bifurcation analysis of the Rose–Hindmarsh model, Chaos Soliton. Fract., 2005, 23(5), 1643–1649. [23] P. C. Rech, Dynamics of a neuron model in different two-dimensional parameter-spaces, Phys. Lett. A, 2011, 375(12), 1461–1464. [24] M. Storace, D. Linaro and E. de Lange, The Hindmarsh–Rose neuron model: bifurcation analysis and piecewise-linear approximations, Chaos, 2008, 18(3), 033128–1–10. [25] E. V. Varenikova, Reflecting function and solutions of two-point boundary value problems for nonautonomous two-dimensional differential systems, Diff. Eqs., 2012, 48(1), 147–152. [26] X. Wang, Genesis of bursting oscillations in the Hindmarsh–Rose model and homoclinicity to a chaotic saddle, Phys. D, 1993, 62(1), 263–274. [27] Z. Wang and X. Shi, Chaotic bursting lag synchronization of Hindmarsh–Rose system via a single controller, Appl. Math. Comput., 2009, 215(3), 1091–1097. [28] Wolfram Research, Inc., Mathematica, Version 11.1. Champaign, IL, 2017. [29] J. Zhou, The differential systems with the same reflecting function, Appl. Math. Comput., 2011, 218(7), 3144–3148. [30] Z. Zhou, F. Mao and Y. Yan, Research on the Poincaré center-focus problem of some cubic differential systems by using a new method, Adv. Diff. Equ., 2017, 2017(1), 52–1–14. -
-
-
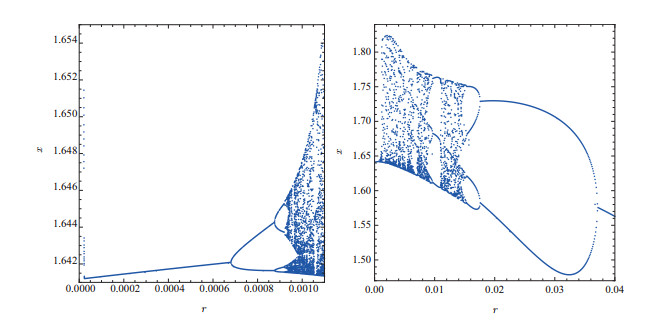
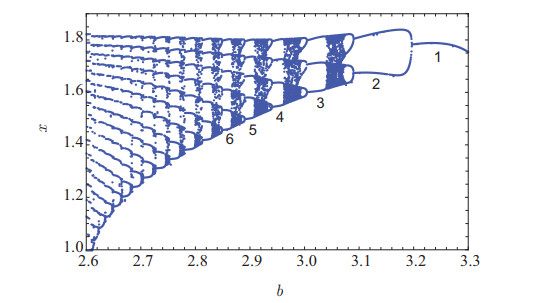
Figure 1.
Bifurcation diagram of the system (2.2) depicting local maxima
$ x $ $ b $ $ I=-3.4b+13.24 $ -
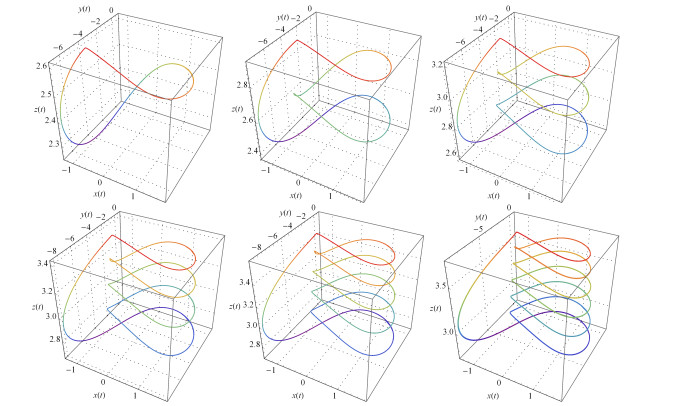
Figure 2.
Periodic attractors of the system (2.2) for
$ b=3.25 $ $ I=2.19 $ $ b=3.15 $ $ I=2.53 $ $ b=3.02 $ $ I=2.972 $ $ b=2.95 $ $ I=3.21 $ $ b=2.9 $ $ I=3.38 $ $ b=2.85 $ $ I=3.55 $ -
Figure 3.
Bifurcation diagram of the system (2.2) depicting local maxima
$ x $ $ r $ $ 0\le r\le 0.0011 $ -
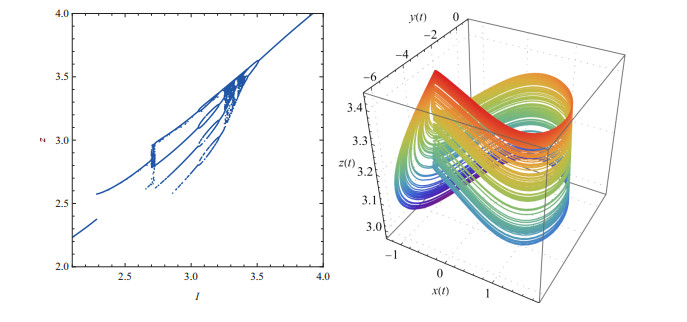
Figure 4.
Bifurcation diagram of the system (2.2) depicting local maxima
$ z $ $ I $ -
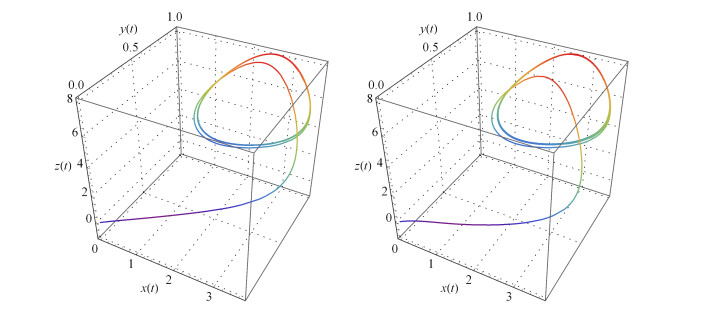
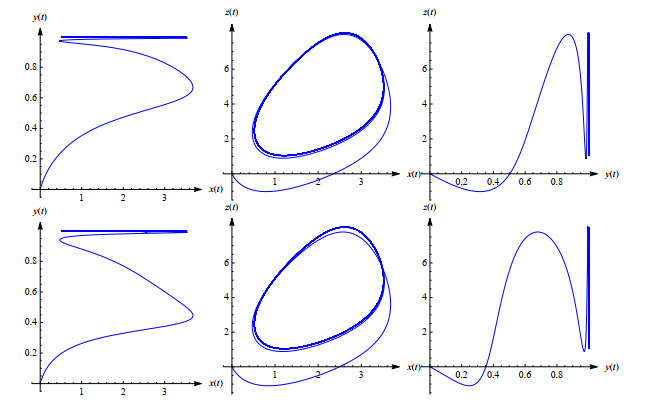
Figure 5.
Solution of the systems (2.1) and (2.3) (left and right respectively) in the phase space.
-
Figure 6.
Phase planes projections of the solution of the systems (2.1) and (2.3) (top and bottom rows respectively).
-
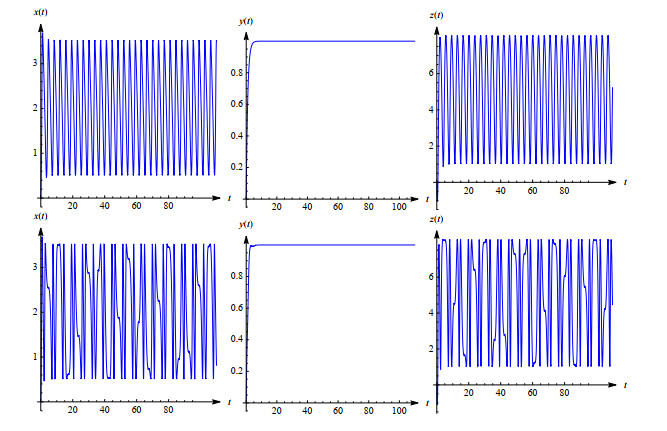
Figure 7.
Solution components of the system (2.1) and (2.3) (top and bottom rows respectively).




 DownLoad:
DownLoad: