| Citation: |
Junsheng Duan, Randolph Rach, Dichen Hu. HIGH ACCURACY PIECEWISE-ANALYTIC SOLUTIONS AND HIGHER-ORDER NUMERIC SOLUTIONS OF PROJECTILE MOTION WITH A QUADRATIC DRAG FORCE BY THE MULTISTAGE MODIFIED DECOMPOSITION METHOD[J]. Journal of Applied Analysis & Computation, 2023, 13(4): 1679-1701. doi: 10.11948/20210277
|
HIGH ACCURACY PIECEWISE-ANALYTIC SOLUTIONS AND HIGHER-ORDER NUMERIC SOLUTIONS OF PROJECTILE MOTION WITH A QUADRATIC DRAG FORCE BY THE MULTISTAGE MODIFIED DECOMPOSITION METHOD
-
Abstract
We apply the multistage modified decomposition method (MDM) of Rach, Adomian, and Meyers to simulate the atmospheric projectile trajectory subject to a quadratic drag force. We readily obtain both the approximate analytic and numeric solutions through means of one-step recurrence algorithms based on the concept of analytic continuation, where the step size $ h $ and the order $ m $ are used to control errors. Simply put, the numeric solutions become the nodal values of our piecewise-analytic approximations. The realistic mathematical model includes sinusoidal, quadratic, reciprocal, and product nonlinearities which are conveniently treated by the Adomian polynomials without resort to any linearization or perturbation whatsoever. Fast algorithms of the Adomian polynomials guarantee the efficiency of our approach, and both the approximate analytic and numeric higher-order solutions can be readily generated at will unlike the usual Runge-Kutta methods that rely on a crude linearization. Multistage analytic and numeric decomposition algorithms demonstrate the rapid convergence of our new approach, where the MDM is based on the nonlinear transformation of series by the Adomian-Rach theorem. As an example, we also determine several important aerodynamic measures for the trajectory of a baseball such as the time of ascent, the velocity at the trajectory apex, the maximum height of ascent, then the flight range, the impact velocity and the impact angle with respect to the horizontal, the optimal launch angle, and the maximum flight range. We consider the error analyses for the multistage analytic approximations including the remainder error functions and also introduce the accumulative remainder error functions and the accumulative remainder error bounds for the numeric solutions. Our approximate solutions compare most favorably to the exact solution by Bernoulli.
-
-
References
[1] K. Abbaoui, Y. Cherruault and V. Seng, Practical formulae for the calculus of multivariable Adomian polynomials, Math. Comput. Modelling, 1995, 22, 89–93. [2] F. Abdelwahid, A mathematical model of Adomian polynomials, Appl. Math. Comput., 2003, 141, 447–453. [3] G. Adomian, Nonlinear Stochastic Operator Equations, Academic, Orlando, FL, 1986. [4] G. Adomian, Nonlinear Stochastic Systems Theory and Applications to Physics, Kluwer Academic, Dordrecht, 1989. [5] G. Adomian, Solving Frontier Problems of Physics: The Decomposition Method, Kluwer Academic, Dordrecht, 1994. [6] G. Adomian and R. Rach, Inversion of nonlinear stochastic operators, J. Math. Anal. Appl., 1983, 91, 39–46. [7] G. Adomian and R. Rach, Transformation of series, Appl. Math. Lett., 1991, 4, 69–71. [8] G. Adomian and R. Rach, Generalization of Adomian polynomials to functions of several variables, Comput. Math. Appl., 1992, 24, 11–24. [9] G. Adomian and R. Rach, Modified decomposition solution of nonlinear partial differential equations, Appl. Math. Lett., 1992, 5, 29–30. [10] G. Adomian and R. Rach, Nonlinear transformation of series–Part Ⅱ, Comput. Math. Appl., 1992, 23, 79–83. [11] G. Adomian and R. Rach, Modified decomposition solution of linear and nonlinear boundary-value problems, Nonlinear Anal., 1994, 23, 615–619. [12] G. Adomian, R. Rach and N. T. Shawagfeh, On the analytic solution of the Lane-Emden equation, Found. Phys. Lett., 1995, 8, 161–181. [13] M. Azreg-Aïnou, A developed new algorithm for evaluating Adomian polynomials, CMES-Comput. Model. Eng. Sci., 2009, 42, 1–18. [14] P. Chudinov, Approximate analytical description of the projectile motion with a quadratic drag force, Athens J. Sci., 2014, 1(2), 97–106. [15] P. Chudinov, V. Eltyshev and Y. Barykin, Simple and convenient analytical formulas for studying the projectile motion in midair, Rev. Bras. de Ens. de Física, 2018, 40(1), e1308. [16] P. Chudinov, V. Eltyshev and Y. Barykin, Analytical construction of the projectile motion trajectory in midair, Revista de Física, 2021, 62, 79–96. [17] P. S. Chudinov, The motion of a heavy particle in a medium with quadratic drag force, Int. J. Nonlinear Sci. Numer. Simul., 2002, 3, 121–129. [18] C. Cohen, B. Darbois-Texier, G. Dupeux et al., The aerodynamic wall, Proc. R. Soc. A, 2014, 470, 20130497. [19] R. Cross, Physics of Baseball and Softball, Springer, New York, 2011. [20] J. S. Duan, An efficient algorithm for the multivariable Adomian polynomials, Appl. Math. Comput., 2010, 217, 2456–2467. [21] J. S. Duan, Recurrence triangle for Adomian polynomials, Appl. Math. Comput., 2010, 216, 1235–1241. [22] J. S. Duan, Convenient analytic recurrence algorithms for the Adomian polynomials, Appl. Math. Comput., 2011, 217, 6337–6348. [23] J. S. Duan, T. Chaolu and R. Rach, Solutions of the initial value problem for nonlinear fractional ordinary differential equations by the Rach-Adomian-Meyers modified decomposition method, Appl. Math. Comput., 2012, 218, 8370–8392. [24] J. S. Duan and R. Rach, New higher-order numerical one-step methods based on the Adomian and the modified decomposition methods, Appl. Math. Comput., 2011, 218, 2810–2828. [25] J. S. Duan, R. Rach and A. M. Wazwaz, A new modified Adomian decomposition method for higher-order nonlinear dynamical systems, CMES-Comput. Model. Eng. Sci., 2013, 94, 77–118. [26] J. S. Duan, R. Rach and A. M. Wazwaz, Higher order numeric solutions of the Lane-Emden-type equations derived from the multi-stage modified Adomian decomposition method, Int. J. Comput. Math., 2017, 94(1), 197–215. [27] J. S. Duan, R. Rach and A. M. Wazwaz, Simulation of the eigenvalue problem for tapered rotating beams by the modified decomposition method, Int. J. Comput. Methods Eng. Sci. Mech., 2022, 23, 20–28. [28] J. C. Hsu, H. Y. Lai and C. K. Chen, An innovative eigenvalue problem solver for free vibration of uniform Timoshenko beams by using the Adomian modified decomposition method, J. Sound Vibration, 2009, 325, 451–470. [29] R. Kantrowitz and M. M. Neumann, Parabolic sandwiches for functions on a compact interval and an application to projectile motion, Int. J. Math. Math. Sci., 2019, 2019, 4868106. [30] R. Rach, A convenient computational form for the Adomian polynomials, J. Math. Anal. Appl., 1984, 102, 415–419. [31] R. Rach, A new definition of the Adomian polynomials, Kybernetes, 2008, 37, 910–955. [32] R. Rach, A bibliography of the theory and applications of the Adomian decomposition method, 1961-2011, Kybernetes, 2012, 41, 1087–1148. [33] R. Rach, G. Adomian and R. E. Meyers, A modified decomposition, Comput. Math. Appl., 1992, 23, 17–23. [34] R. Rach, J. S. Duan and A. M. Wazwaz, Simulation of large deflections of a flexible cantilever beam fabricated from functionally graded materials by the Adomian decomposition method, Int. J. Dyn. Syst. Differ. Equ., 2020, 10(4), 287–298. [35] S. E. Serrano, Differential Equations: Applied Mathematical Modeling, Nonlinear Analysis, and Computer Simulation in Engineering and Science, HydroScience Inc., Ambler, PA, 2016. [36] P. Timmerman and J. P. van der Weele, On the rise and fall of a ball with linear or quadratic drag, Am. J. Phys., 1999, 67(6), 538–546. [37] M. Turkyilmazoglu, Highly accurate analytic formulae for projectile motion subjected to quadratic drag, Eur. J. Phys., 2016, 37, 035001. [38] A. Vial, Horizontal distance travelled by a mobile experiencing a quadratic drag force: normalized distance and parametrization, Eur. J. Phys., 2007, 28, 657–663. [39] R. D. H. Warburton, J. Wang and J. Burgdörfer, Analytic approximations of projectile motion with quadratic air resistance, J. Serv. Sci. Manag., 2010, 3, 98–105. [40] A. M. Wazwaz, A new algorithm for calculating Adomian polynomials for nonlinear operators, Appl. Math. Comput., 2000, 111, 53–69. [41] A. M. Wazwaz, Linear and Nonlinear Integral Equations: Methods and Applications, Higher Education Press, Beijing, and Springer-Verlag, Berlin, 2011. [42] Y. Zhu, Q. Chang and S. Wu, A new algorithm for calculating Adomian polynomials, Appl. Math. Comput., 2005, 169, 402–416. -
-
Figures(21) / Tables(3)
Export File
Citation
Junsheng Duan, Randolph Rach, Dichen Hu. HIGH ACCURACY PIECEWISE-ANALYTIC SOLUTIONS AND HIGHER-ORDER NUMERIC SOLUTIONS OF PROJECTILE MOTION WITH A QUADRATIC DRAG FORCE BY THE MULTISTAGE MODIFIED DECOMPOSITION METHOD[J]. Journal of Applied Analysis & Computation, 2023, 13(4): 1679-1701. doi: 10.11948/20210277
Format
Content
DownLoad:
-
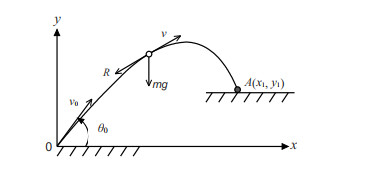
Figure 1.
Schematic diagram of a moving projectile.
-
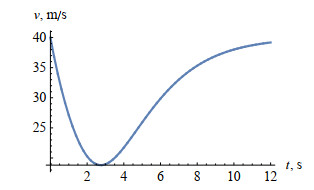
Figure 2.
Solution
$ \Phi _{v, m + 1}(t) $ $ 0\leq t\leq 12 $ -
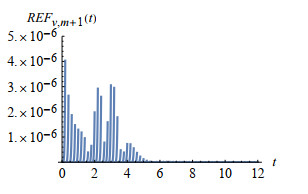
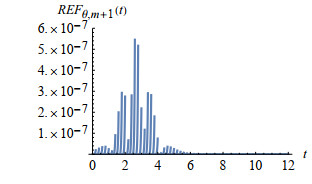
Figure 3.
Remainder error function
$ REF_{v, m+1}(t) $ -
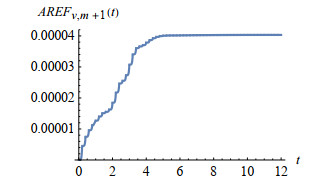
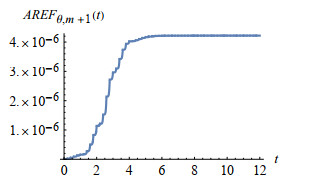
Figure 4.
Accumulative remainder error function
$ AREF_{v, m+1}(t) $ -
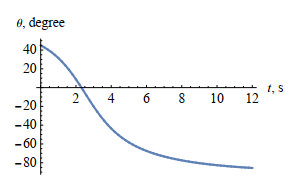
Figure 5.
Solution
$ \Phi _{\theta, m + 1}(t) $ $ 0\leq t\leq 12 $ -
Figure 6.
Remainder error function
$ REF_{\theta, m+1}(t) $ -
Figure 7.
Accumulative remainder error function
$ AREF_{\theta, m+1}(t) $ -
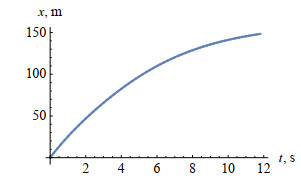
Figure 8.
Solution
$ \Phi _{x, m + 1}(t) $ $ 0\leq t\leq 12 $ -
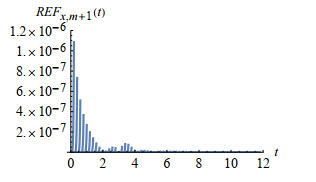
Figure 9.
Remainder error function
$ REF_{x, m+1}(t) $ -
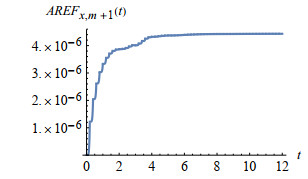
Figure 10.
Accumulative remainder error function
$ AREF_{x, m+1}(t) $ -
Figure 11.
Solution
$ \Phi _{y, m + 1}(t) $ $ 0\leq t\leq 12 $ -
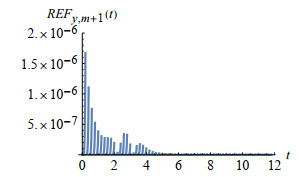
Figure 12.
Remainder error function
$ REF_{y, m+1}(t) $ -
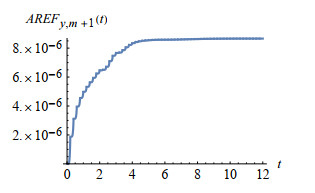
Figure 13.
Accumulative remainder error function
$ AREF_{y, m+1}(t) $ -
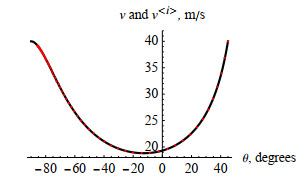
Figure 14.
Comparison of the exact value (solid line) and numeric results (dots) of
$ v $ $ \theta $ -
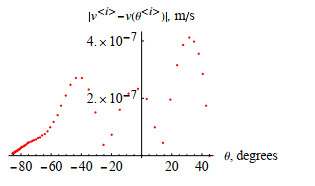
Figure 15.
Absolute errors of the numeric solutions
$ v^{\langle i\rangle} $ $ \theta $ -
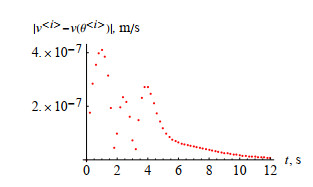
Figure 16.
Absolute errors of the numeric solutions
$ v^{\langle i\rangle} $ $ t $ -
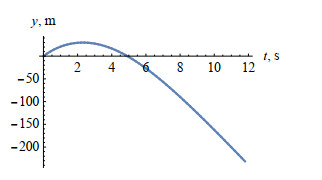
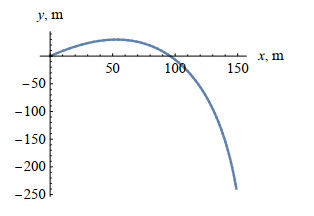
Figure 17.
Curve of the Cartesian coordinates
$ y $ $ x $ -
Figure 18.
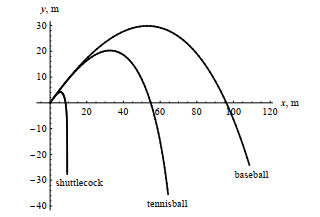
Trajectories of a baseball, tennisball and shuttlecock for
$ v_0=40\; {\rm m/s} $ $ \theta_0=45^\circ $ -
Figure 19.
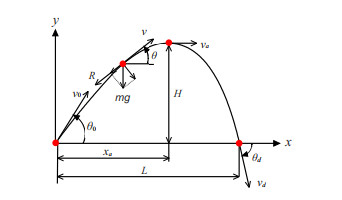
Schematic diagram for the flight range with the impact point on the horizontal line
$ y=y_1 $ -
Figure 20.
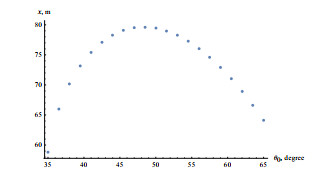
Plots of the horizontal flight range versus the launch angle
$ \theta_0 $ $ ^\circ $ $ ^\circ $ -
Figure 21.
Plots of the horizontal flight range versus the launch angle
$ \theta_0 $ $ ^\circ $ $ ^\circ $