| Citation: |
Yanfei Zhao, Yepeng Xing. A DYNAMIC MODEL FOR COVID-19 THERAPY WITH DEFECTIVE INTERFERING PARTICLES AND ARTIFICIAL ANTIBODIES[J]. Journal of Applied Analysis & Computation, 2021, 11(5): 2611-2629. doi: 10.11948/20210102
|
A DYNAMIC MODEL FOR COVID-19 THERAPY WITH DEFECTIVE INTERFERING PARTICLES AND ARTIFICIAL ANTIBODIES
-
Abstract
In this paper, we use ordinary differential equations to propose a mathematical model for COVID-19 therapy with both defective interfering particles and artificial antibodies. For this model, the basic reproduction number R0 is given and its threshold properties are discussed. We investigate the global asymptotic stability of disease-free equilibrium E0 and infection equilibrium without defective interfering particles E1 by utilizing Lyapunov function and LaSalleos invariance principle. For infection equilibrium with defective interfering particles E2, stability and Hopf bifurcation results are presented. Numerical simulation is also given to demonstrate the applicability of the theoretical predictions.
-
-
References
[1] S. F. Ahmed, A. A. Quadeer and M. R. McKay, Preliminary identification of potential vaccine targets for the COVID-19 coronavirus (SARS-CoV-2) based on SARS-CoV immunological studies, Viruses, 2020, 12(3), 254. doi: 10.3390/v12030254 [2] R. M. Anderson and R. M. May, Infectious diseases of humans: dynamics and control, Oxford university press, Oxford, 1992. [3] P. Chen, A. Nirula, B. Heller et al., SARS-CoV-2 neutralizing antibody LYCoV555 in outpatients with COVID-19, New England Journal of Medicine, 2021, 384(3), 229–237. doi: 10.1056/NEJMoa2029849 [4] P. H. Duesberg, The RNA of influenza virus, Proceedings of the National Academy of Sciences of the United States of America, 1968, 59(3), 930. doi: 10.1073/pnas.59.3.930 [5] F. R. Gantmacher and J. L. Brenner, Applications of the Theory of Matrices, Courier Corporation, New York, 2005. [6] L. E. Gralinski and V. D. Menachery, Return of the coronavirus: 2019-nCoV, Viruses, 2020, 12(2), 135. doi: 10.3390/v12020135 [7] J. J. Holland, S. I. T. Kennedy, B. L. Semler et al., Defective interfering RNA viruses and the host-cell response, Springer, 1980. DOI: 10.1007/978-1-4613- 3129-2. [8] X. Jiang, P. Yu, Z. Yuan and X. Zou, Dynamics of an HIV-1 therapy model of fighting a virus with another virus, Journal of Biological Dynamics, 2009, 3(4), 387–409. doi: 10.1080/17513750802485007 [9] R. L. Kruse, Therapeutic strategies in an outbreak scenario to treat the novel coronavirus originating in Wuhan, China, F1000Research, 2020. DOI: 10- 12688/f1000research-22211-2. [10] J. P. La Salle, The stability of dynamical systems, SIAM, Philadelphia, 1976. [11] Q. Li, X. Guan, P. Wu et al., Early transmission dynamics in Wuhan, China, of novel coronavirus-infected pneumonia, New England journal of medicine, 2020. DOI: 10-1056/NEJMoa2001316. [12] W. Li, M. J. Moore, N. Vasilieva et al., Angiotensin-converting enzyme 2 is a functional receptor for the SARS coronavirus, Nature, 2003, 426(6965), 450– 454. doi: 10.1038/nature02145 [13] P. W. Nelson, J. E. Mittler and A. S. Perelson, Effect of drug efficacy and the eclipse phase of the viral life cycle on estimates of HIV viral dynamic parameters, Journal of acquired immune deficiency syndromes (1999), 2001, 26(5), 405–412. doi: 10.1097/00042560-200104150-00002 [14] M. Pashaei and N. Rezaei, Immunotherapy for SARS-CoV-2: potential opportunities, Expert opinion on biological therapy, 2020, 20(10), 1111–1116. doi: 10.1080/14712598.2020.1807933 [15] U. Rand, S. Y. Kupke, H. Shkarlet et al., Antiviral activity of influenza a virus defective interfering particles against SARS-CoV-2 replication in vitro through stimulation of innate immunity, bioRxiv, 2021. DOI: 10-1101/2021- 02-19-431972. [16] W. Shang, Y. Yang, Y. Rao and X. Rao, The outbreak of SARS-CoV-2 pneumonia calls for viral vaccines, npj Vaccines, 2020, 5(1), 1-3. doi: 10.1038/s41541-019-0151-3 [17] Y. Shi, G. Wang, X. Cai et al., An overview of COVID-19, Journal of Zhejiang University. Science. B, 2020, 21(5), 343–360. doi: 10.1631/jzus.B2000083 [18] F. Tapia, T. Laske, M. A. Wasik et al., Production of defective interfering particles of influenza a virus in parallel continuous cultures at two residence timesinsights from QPCR measurements and viral dynamics modeling, Frontiers in bioengineering and biotechnology, 2019. DOI: 10-3389/fbioe-2019-00275. [19] M. A. Tortorici and D. Veesler, Structural insights into coronavirus entry, Advances in virus research, 2019, 105(4), 93–116. [20] M. Vignuzzi and C. B. López, Defective viral genomes are key drivers of the virus-host interaction, Nature microbiology, 2019, 4(7), 1075–1087. doi: 10.1038/s41564-019-0465-y [21] M. A. Wasik, L. Eichwald, Y. Genzel and U. Reichl, Cell culture-based production of defective interfering particles for influenza antiviral therapy, Applied microbiology and biotechnology, 2018, 102(3), 1167–1177. doi: 10.1007/s00253-017-8660-3 [22] Y. C. Wu, C. S. Chen and Y. J. Chan, The outbreak of COVID-19: an overview, Journal of the Chinese medical association, 2020, 83(3), 217–218. doi: 10.1097/JCMA.0000000000000270 [23] P. Yu, Closed-form conditions of bifurcation points for general differential equations, International Journal of Bifurcation and Chaos, 2005, 15(04), 1467–1483. doi: 10.1142/S0218127405012582 [24] P. Yu, J. Huang and J. Jiang, Dynamics of an HIV-1 infection model with cell mediated immunity, Communications in Nonlinear Science and Numerical Simulation, 2014, 19(10), 3827–3844. doi: 10.1016/j.cnsns.2014.03.002 [25] H. Zhao, K. K. To, H. Chu et al., Dual-functional peptide with defective interfering genes effectively protects mice against avian and seasonal influenza, Nature communications, 2018, 9(1), 1–14. doi: 10.1038/s41467-017-02088-w -
-
Figures(6)
Export File
Citation
Yanfei Zhao, Yepeng Xing. A DYNAMIC MODEL FOR COVID-19 THERAPY WITH DEFECTIVE INTERFERING PARTICLES AND ARTIFICIAL ANTIBODIES[J]. Journal of Applied Analysis & Computation, 2021, 11(5): 2611-2629. doi: 10.11948/20210102
Format
Content
DownLoad:
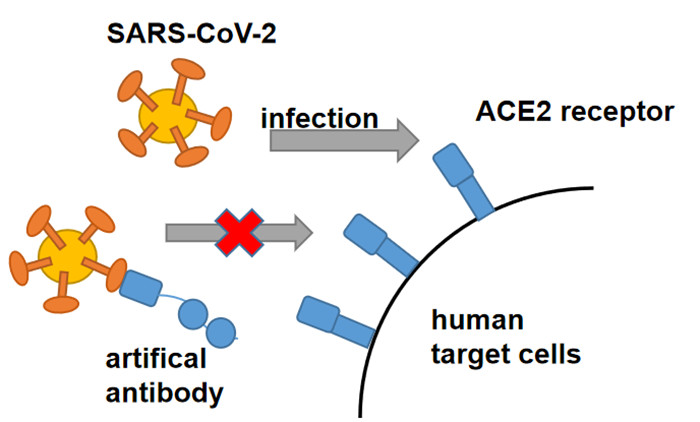
- Figure 1. Artificial antibodies block SARS-CoV-2 from infecting cells.
-
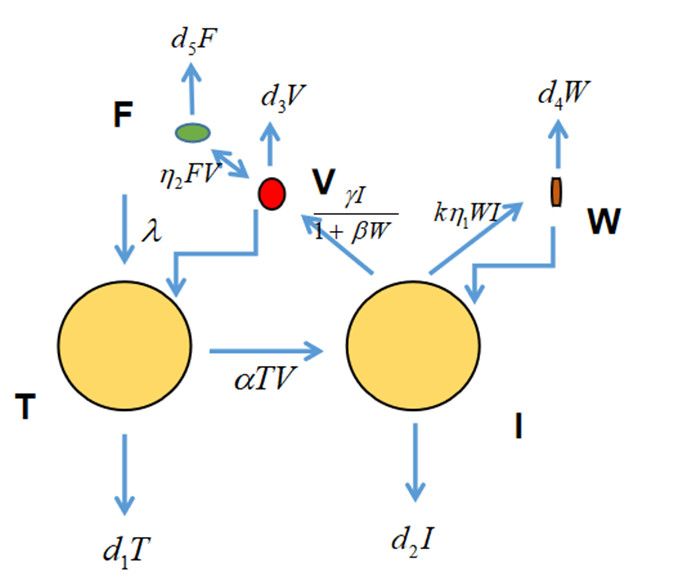
Figure 2. Pathogen viral particles
$ V $ infect normal cells$ T $ , producing infected cells$ I $ ;$ W $ can infect infected cells, artificial antibodies$ F $ bind to virus, infected cells are able to produce virus$ V $ and defective interfering particles$ W $ . -
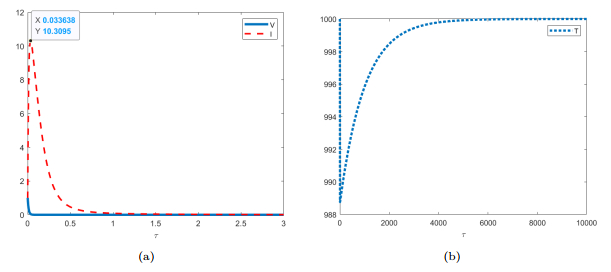
Figure 3. Simulation of system (3.16) for the parameter values given in (4.1) and
$ \gamma = \dfrac{1}{2000} $ , showing that solution trajectories converge to the disease-free equilibrium$ E_0 $ . -
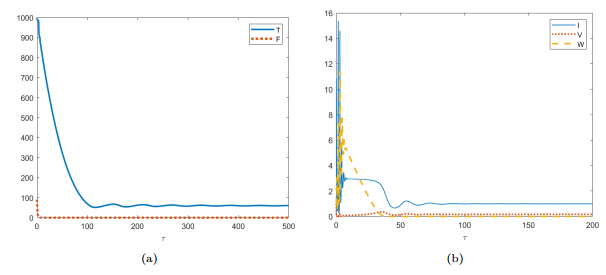
Figure 4. Simulation of system (3.16) for the parameter values given in (4.1) and
$ \gamma = 1/20 $ , showing that solution trajectories converge to the infection equilibrium without defective interefering particles$ E_1 $ . -
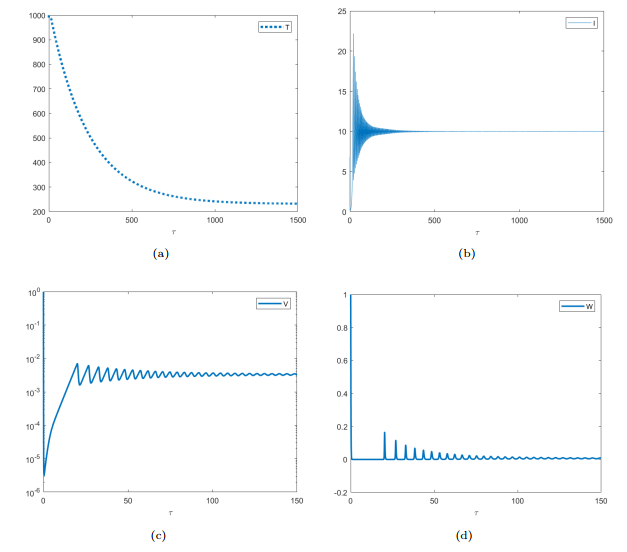
Figure 5. Simulation of system (3.16) for the parameter values given in (4.3) and
$ \gamma = 1/1000 $ , showing that solution trajectories converge to the infection equilibrium with defective interefering particles$ E_2 $ . -
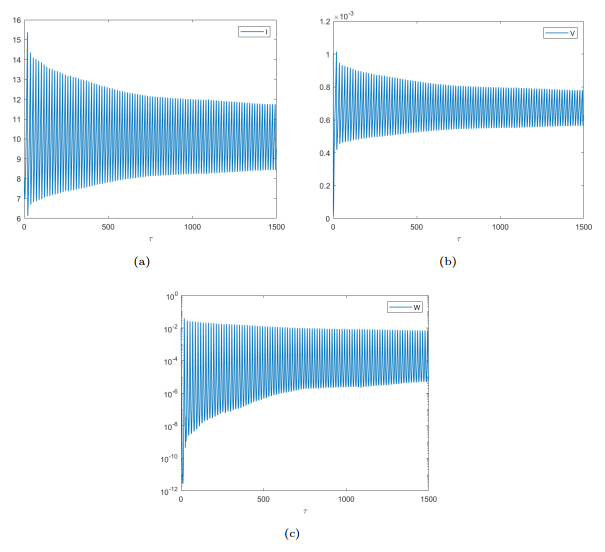
Figure 6. Simulation of system (3.16) for the parameter values given in (4.3) and
$ \gamma = 0.0002 $ , showing that periodic solutions.