| Citation: |
Francisco Ortegón Gallego, Mohamed Rhoudaf, Hajar Talbi. CAPACITY SOLUTION AND NUMERICAL APPROXIMATION TO A NONLINEAR COUPLED ELLIPTIC SYSTEM IN ANISOTROPIC SOBOLEV SPACES[J]. Journal of Applied Analysis & Computation, 2022, 12(6): 2184-2207. doi: 10.11948/20210208
|
CAPACITY SOLUTION AND NUMERICAL APPROXIMATION TO A NONLINEAR COUPLED ELLIPTIC SYSTEM IN ANISOTROPIC SOBOLEV SPACES
-
Abstract
In this paper, we analyze the existence and the numerical simulation of a capacity solution to a coupled nonlinear elliptic system, whose unknowns are the temperature inside a semiconductor material $u$, and the electric potential $\varphi$. The model problem we refer to is
$ \left\{\begin{array}{ll} -\Delta_{\vec{p}}\, u =\rho(u)|\nabla \varphi|^{2} & \text { in } \Omega \ \\ \operatorname{div}(\rho(u) \nabla \varphi)=0 & \text { in } \Omega \ \\ \varphi=\varphi_{0} & \text { on } \partial \Omega \ \\ u=0 & \text { on } \partial \Omega \end{array}\right. $
where $\Omega$ is an open bounded set of $\mathbb{R}^N$, $N\geq2$ and $\Delta_{\vec{p}}\, u=\mathop {\mathop \sum \limits_{i = 1} }\limits^N \partial_i\left( |\partial_i u|^{p_i-2}\partial_i u \right)$, is the $\vec{p}-$Laplacian operator. We consider the case of a nonuniformly elliptic problem.
-
-
References
[1] R. Adams, Sobolev Spaces, Press, New York, 1975. [2] S. Antontsev and M. Chipot, Anisotropic equations: uniqueness and existence results, Differ. Integr. Equations, 2008, 21(5-6), 401–419. [3] S. Antontsev and M. Chipot, The thermistor problem: existence, smoothness, uniqueness, blowup, SIAM J. Math. Anal., 1994, 25(4), 1128–1156. doi: 10.1137/S0036141092233482 [4] M. Bahari, R. Elarabi, and M. Rhoudaf, Existence of capacity solution for a perturbed nonlinear coupled system, J. Elliptic. Parabol. Equ., 2021, 7(1), 101–119. doi: 10.1007/s41808-021-00097-x [5] J. Barret and W. B. Liu, Finite element approximation of the $p$-Laplacian, Math. Comput., 1993, 61(204), 523–537. [6] J. Barret and W. B. Liu, Finite element approximation of the parabolic $p$-Laplacian, SIAM J. Numer. Anal. 1994, 31, 413–428. doi: 10.1137/0731022 [7] M. Bendahmane, M. Chrif and S. El Manouni, An approximation result in generalized anisotropic Sobolev spaces and applications, Z. Anal. Anwend., 2011, 30, 341–353. [8] H. Brezis, Functional Analysis, Sobolev Spaces and Partial Differential Equations, Springer, New York, 2011. [9] M. Chrif and S. El Manouni, On a strongly anisotropic equation with $L^1$ data, Appl. Anal., 2008, 87(7), 865–871. doi: 10.1080/00036810802307546 [10] M. Cimatti and G. Prodi, Existence results for a nonlinear elliptic system modelling a temperature dependent electrical resistor, Ann. Mat. Pura Appl., 1998, 63, 227–236. [11] M. T. González Montesinos and F. Ortegón Gallego, Existence of a capacity solution to a coupled nonlinear parabolic-elliptic system, Commun. Pure Appl. Anal., 2007, 6(1), 23–42. doi: 10.3934/cpaa.2007.6.23 [12] M. T. González Montesinos and F. Ortegón Gallego, The thermistor problem with degenerate thermal conductivity and metallic conduction, Discrete Contin. Dyn. Syst., 2007, 2007 (Special), 446–455. [13] M. Ghilani, E. H. Quenjel and M. Rhoudaf, Numerical Analysis of a Stable Finite Volume Scheme for a Generalized Thermistor Model, Comput. Methods Appl. Math., 2021, 21(1), 69–87. doi: 10.1515/cmam-2019-0144 [14] F. Hecht, The Mesh Adapting Software: BAMG, INRIA Report, vol. 250, 1998. [15] F. Hecht, New development in Freefem++, J. Numer. Math., 2012, 20(3-4), 251–265. [16] H. Moussa, F. Ortegón Gallego and M. Rhoudaf, Capacity solution to a coupled system of parabolic-elliptic equations in Orlicz-Sobolev spaces, Nonlinear Differ. Equ. Appl., 2018, 25(14), 1–37. [17] H. Moussa, F. Ortegón Gallego and M. Rhoudaf, Capacity solution to a nonlinear elliptic coupled system in Orlicz-Sobolev spaces, Mediterr. J. Math., 2020, 17(67), 1–28. [18] F. Ortegón Gallego, M. Rhoudaf and H. Sabiki, On a nonlinear parabolic-elliptic system in Musielak-Orlicz spaces, Electron. J. Differ. Equ., 2018, 121, 1–36. [19] X. Xu, A degenerate Stefan-like problem with Joule's heating, SIAM J. Math. Anal., 1992, 23, 1417–1438. doi: 10.1137/0523081 [20] X. Xu, A strongly degenerate system involving an equation of parabolic type and an equation of elliptic type, Comm. Partial Differential Equations 1993, 18, 199–213. doi: 10.1080/03605309308820927 [21] X. Xu, On the existence of bounded temperature in the thermistor problem with degeneracy. Nonlinear Anal. : T. M. A., 2000, 42(2), 199–213. doi: 10.1016/S0362-546X(98)00340-X [22] X. Xu, Local regularity theorems for the stationary thermistor problem with oscillating degeneracy, J. Math. Anal. Appl., 2008, 338(1), 274–284. doi: 10.1016/j.jmaa.2007.05.025 -
-
Figures(4) / Tables(3)
Export File
Citation
Francisco Ortegón Gallego, Mohamed Rhoudaf, Hajar Talbi. CAPACITY SOLUTION AND NUMERICAL APPROXIMATION TO A NONLINEAR COUPLED ELLIPTIC SYSTEM IN ANISOTROPIC SOBOLEV SPACES[J]. Journal of Applied Analysis & Computation, 2022, 12(6): 2184-2207. doi: 10.11948/20210208
Format
Content
DownLoad:
-
Figure 1. Initial triangulation of
$ \Omega $ . -
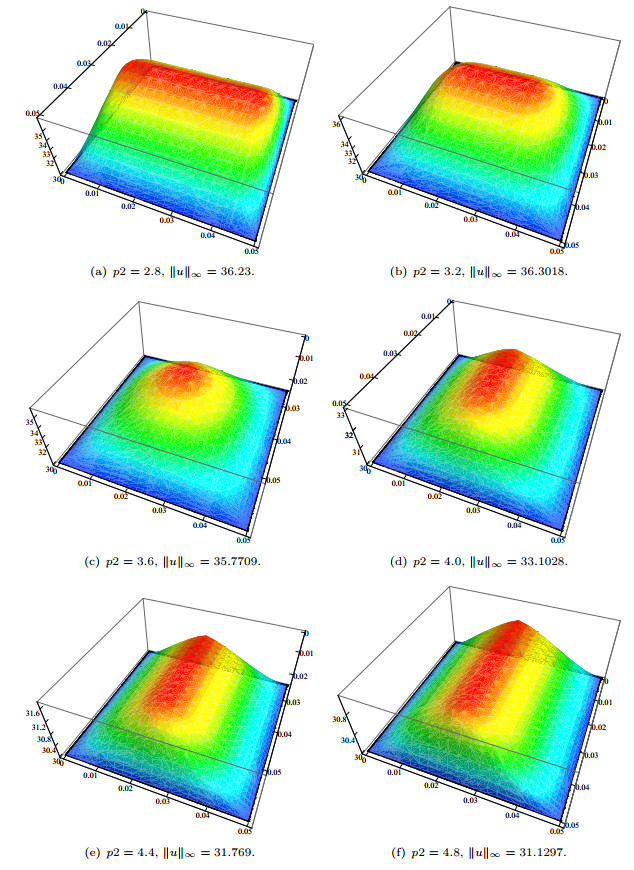
Figure 2. Distribution of the temperature
$ u $ for$ p_1=3.6 $ and the indicated$ p_2 $ . We took$ \delta=10^{-2} $ and voltage$ V_0=220 $ . -
Figure 3. Final mesh after the adapting technique based on the temperature
$ u $ of Figure 2 for$ p_1=3.6 $ and the indicated$ p_2 $ , respectively, with$ \delta=10^{-2} $ and voltage$ V_0=220 $ V. -
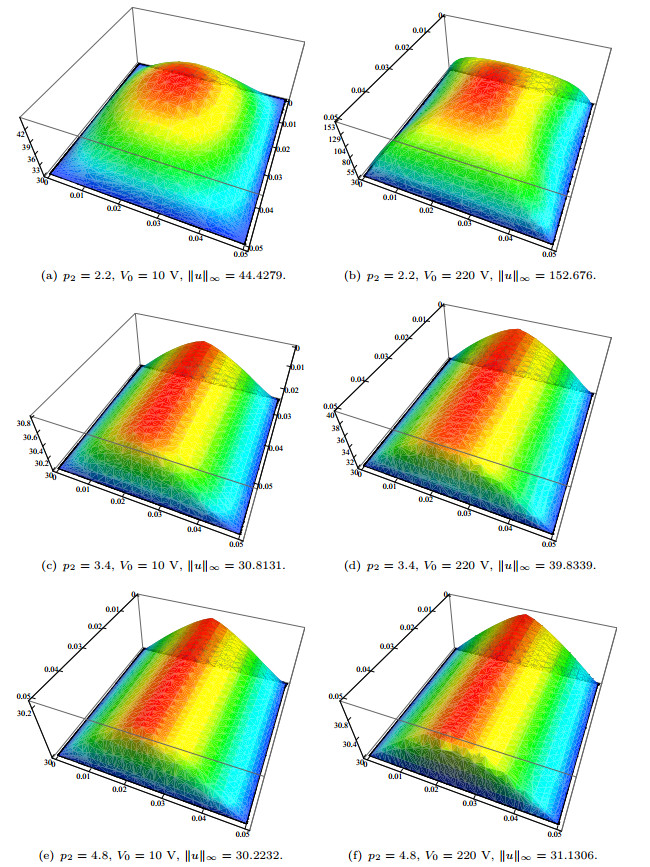
Figure 4. Distribution of the temperature
$ u $ for$ p_1=2.2 $ and the indicated$ p_2 $ . We took$ \delta=10^{-2} $ in all these cases but (b) where$ \delta=10^{-6} $ .