| Citation: |
Rong Liu, Wanbiao Ma, Songbai Guo. REGIME SHIFTS BETWEEN OSCILLATORY PERSISTENCE AND EXTINCTION IN A STOCHASTIC CHEMOSTAT MODEL WITH PERIODIC PARAMETERS[J]. Journal of Applied Analysis & Computation, 2022, 12(4): 1418-1433. doi: 10.11948/20210210
|
REGIME SHIFTS BETWEEN OSCILLATORY PERSISTENCE AND EXTINCTION IN A STOCHASTIC CHEMOSTAT MODEL WITH PERIODIC PARAMETERS
-
Abstract
In this paper, we mechanistically formulate a type of stochastic chemostat model with two complementary nutrients, which is affected by seasonal variations and flocculation effect. The phase transition properties of the model are investigated by theoretical analysis and numerical simulation. The well-posedness of the model is considered. Further, by utilizing Khasminskii's theory, sufficient conditions for the existence of the stochastic nontrivial positive periodic solution are obtained. The existence of the stochastic nontrivial positive periodic solution implies periodic change of microorganism's density. Some sufficient conditions for the global attractivity of the boundary periodic solution of the model are also derived. At last, numerical simulations are performed to illustrate our theoretical results. It is found numerically that the stable positive periodic solution and a stable boundary periodic solution of the model may coexist. Especially, for appropriate random perturbations, the population of the microorganisms changes from an endangered state to an oscillatory persistence state in some regions.
-
-
References
[1] G. J. Butler, S. B. Hsu and P. Waltman, A mathematical model of the chemostat with perodic washout rate, SIAM J. Appl. Math., 1985, 45, 435-49. doi: 10.1137/0145025 [2] Y. Ding, X. Ren, C. Jiang and Q. Zhang, Periodic solution of a stochastic SIQR epidemic model incorporating media coverage, J. Appl. Anal. Comput., 2020, 10(6), 2439-2458. [3] M. Gao, D. Jiang and T. Hayat, Stationary distribution and periodic solution of stochastic chemostat models with single-species growth on two nutrients, Int. J. Biomath., 2019, 6, 23-41. [4] S. B. Hsu, A competition model for a seasonally fluctuating nutrient, J. Math. Biol., 1980, 9, 115-132. doi: 10.1007/BF00275917 [5] R. Khasminskii, Stochastic Stability of Differential Equations, Springer, Heidelberg, 2012. [6] R. Kothari, V. V. Pathak, A. Pandey, S. Ahmad, C. Srivastava and V. V. Tyagi, A novel method to harvest Chlorella sp. via low cost bioflocculant: influence of temperature with kinetic and thermodynamic functions, Bioresource Technol., 2017, 225, 84-89. doi: 10.1016/j.biortech.2016.11.050 [7] R. Liu and W. Ma, Noise-induced stochastic transition: a stochastic chemostat model with two complementary nutrients and flocculation effect, Chaos Solitons Fractals, 2021, 147, 110951. doi: 10.1016/j.chaos.2021.110951 [8] S. Liu, X. Xu, D. Jiang, T. Hayat and B. Ahmad, Stationary distribution and extinction of the DS-I-A model disease with periodic parameter function and markovian switching, Appl. Math. Comput., 2017, 311, 66-84. [9] X. Mao, Stochastic Differential Equations and Applications, Horwood Publishing, Chichester, 1997. [10] X. Meng, L. Wang and T. Zhang, Global dynamics analysis of a nonlinear impulsive stochastic chemostat system in a polluted environment, J. Appl. Anal. Comput., 2016, 6(3), 865-875. [11] H. Peng and X. Zhang, The dynamics of stochastic predator-prey models with non-constant mortality rate and general nonlinear functional response, J. Nonlinear Model. Anal., 2021, 2, 495-511. [12] S. S. Pilyugin and P. Waltman, Competition in the unstirred chemostat with periodic input and washout, SIAM J. Appl. Math., 1999, 59, 1157-1177. doi: 10.1137/S0036139997323954 [13] H. L. Smith, Competitive coexistence in an oscillating chemostat, SIAM J. Appl. Math., 1981, 40, 498-522. doi: 10.1137/0140042 [14] L. Wang, D. Jiang and D. O'Regan, The periodic solutions of a stochastic chemostat model with periodic washout rate, Commun. Nonlinear Sci. Numer. Simul., 2016, 37, 1-13. doi: 10.1016/j.cnsns.2016.01.002 [15] L. Wang and D. Jiang, Periodic solution for the stochastic chemostat with general response function, Physica A, 2017, 486, 378-385. doi: 10.1016/j.physa.2017.05.097 [16] W. Wang, W. Ma and H. Yan, Global dynamics of modeling flocculation of microorganism, Appl. Sci., 2016, 6, 221. doi: 10.3390/app6080221 [17] W. Wang, W. Ma and Z. Feng, Global dynamics and travelling waves for a periodic and diffusive chemostat model with two nutrients and one microorganism, Nonlinearity, 2020, 33, 4338-4380. doi: 10.1088/1361-6544/ab86ca [18] W. Wang and X. Zhao, Threshold dynamics for compartmental epidemic models in periodic environments, J. Dyn. Differ. Equ., 2008, 20, 699-717. doi: 10.1007/s10884-008-9111-8 [19] F. Yang and H. I. Freedman, Competing predators for a prey in a chemostat model with periodic nutrient input, J. Math. Biol., 1991, 29, 715-732. doi: 10.1007/BF00160188 [20] D. Zhao and S. Yuan, Break-even concentration and periodic behavior of a stochastic chemostat model with seasonal fluctuation, Commun. Nonlinear Sci. Numer. Simul., 2017, 46, 62-73. doi: 10.1016/j.cnsns.2016.10.014 [21] X. Zhou, Y. He, H. Li, Y. Wei and X. Chen, Harmful algae using flocculation and subsequent biomanipulation to control microcystis blooms: a laboratory study, Harmful Algae, 2020, 99, 101917. doi: 10.1016/j.hal.2020.101917 -
-
Figures(6)
Export File
Citation
Rong Liu, Wanbiao Ma, Songbai Guo. REGIME SHIFTS BETWEEN OSCILLATORY PERSISTENCE AND EXTINCTION IN A STOCHASTIC CHEMOSTAT MODEL WITH PERIODIC PARAMETERS[J]. Journal of Applied Analysis & Computation, 2022, 12(4): 1418-1433. doi: 10.11948/20210210
Format
Content
DownLoad:
-
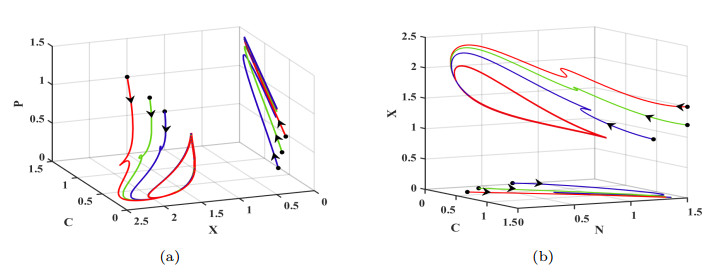
Figure 1. (a) is the phase trajectories of the corresponding deterministic model in the three-dimensional space
$ (C,X,P) $ . (b) is the phase trajectories of the corresponding deterministic model in the three-dimensional space$ (C,N,X) $ .$ [R_{0}]\approx1.785>1 $ . -
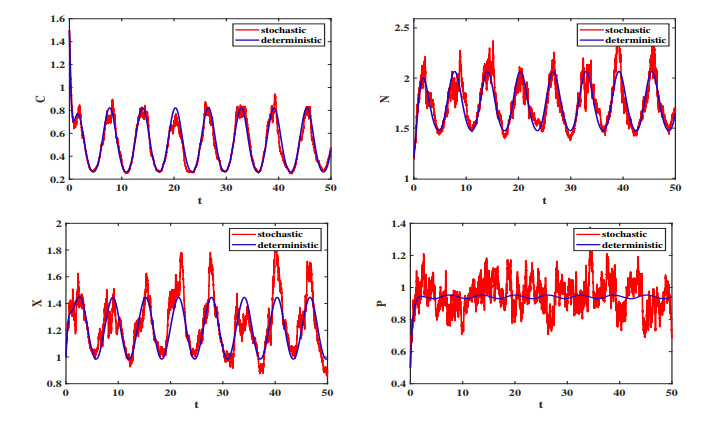
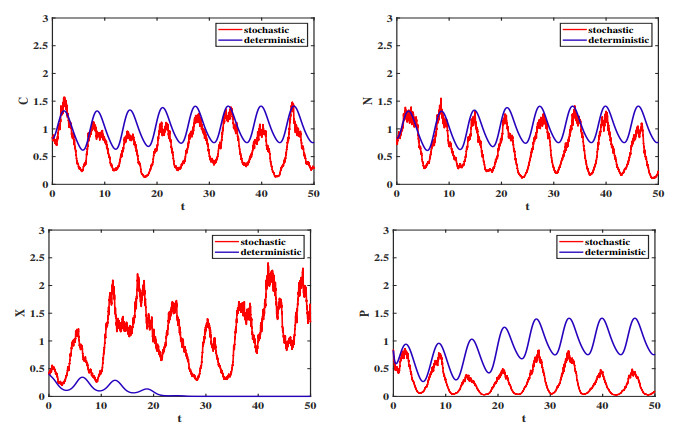
Figure 2. The sample paths of model (1.1) and the solution curves of the corresponding deterministic model.
$ [R_{0}^{s}]\approx1.749>1 $ -
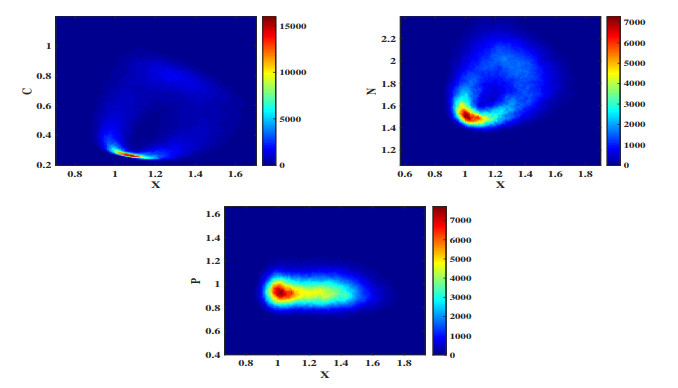
Figure 3. (a), (b), (c) are the path ranges of
$ (X(t),C(t)) $ ,$ (X(t),N(t)) $ ,$ (X(t),P(t)) $ in model (1.1), respectively. The circular areas in the subfigures represent the areas through which the sample paths pass.$ [R_{0}^{s}]\approx1.749>1 $ . -
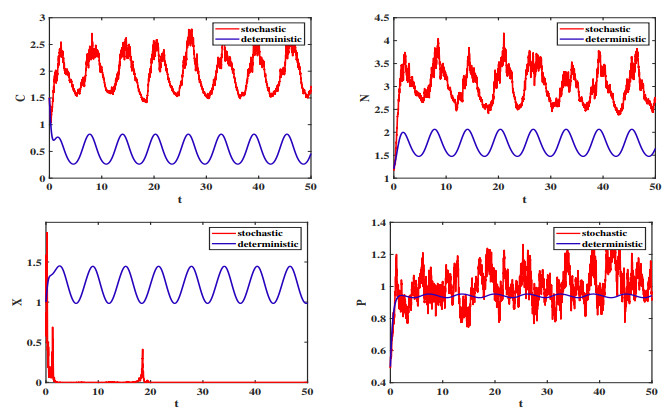
Figure 4. The sample paths of model (1.1) and the solution curves of the corresponding deterministic model.
$ \overline{R_{0}}\approx 0.866<1 $ and$ [R_{0}]\approx1.785>1 $ . -
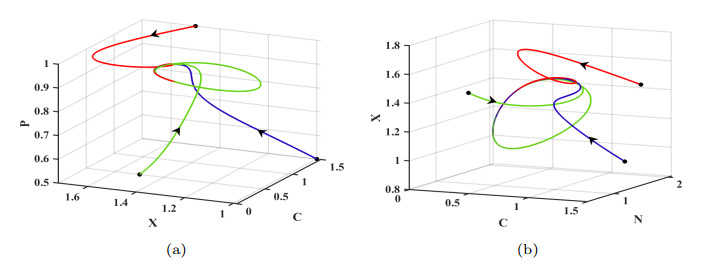
Figure 5. (a) is the phase trajectories of the corresponding deterministic model in the three-dimensional space
$ (C,X,P) $ . (b) is the phase trajectories of the corresponding deterministic model in the three-dimensional space$ (C,N,X) $ . The initial values are given as$ (1.5,1.2,1,0.5) $ ,$ (1.5,1.5,1.2,0.7) $ ,$ (1.5,1.5,1.5,1) $ ,$ (0.5,0.1,0.05,0.5) $ ,$ (0.5,0.2,0.1,0.3) $ and$ (0.5,0.5,0.15,0.1) $ .$ [R_{0}]\approx0.808<1 $ . -
Figure 6. The sample paths of model (1.1) and the solution curves of the corresponding deterministic model. The initial value is taken as
$ (C(0),N(0),X(0),P(0))=(0.83,0.83,0.41,0.83) $ .$ [R_{0}]\approx0.808<1 $ ,$ [R_{0}^{s}]\approx0.681<1 $ and$ \overline{R_{0}}\approx2.357>1 $ .