| Citation: |
Jingnan Wang, Shengnan Liu. PERSISTENCE AND EXTINCTION OF THE TUMOR-IMMUNE STOCHASTIC MODEL WITH EFFECTOR CELLS AND CYTOKINES[J]. Journal of Applied Analysis & Computation, 2023, 13(2): 655-670. doi: 10.11948/20210464
|
PERSISTENCE AND EXTINCTION OF THE TUMOR-IMMUNE STOCHASTIC MODEL WITH EFFECTOR CELLS AND CYTOKINES
-
Abstract
To investigate the effects of microenvironment on the tumor growth and the loss rates of effector cells and cytokine, we present a stochastic tumor-immune model with the treatment response of effector cells assisted by cytokine to tumor growth. By using the comparison theorem, the Itô formula and the law of large numbers, we prove the existence of globally unique positive solution and obtain the sufficient conditions for the extinction and the persistence of tumor cells. Moreover, using our theoretical results, we perform some numerical simulations to show that different noise intensities lead to different states of tumor cells, including tumor extinction and tumor persistence, which confirms the obtained theoretical results and is useful for theoretical guidance of inhibiting tumor growth in clinical medicine.
-
Keywords:
- Stochastic responses /
- Itô formula /
- tumor-immune model /
- extinction /
- persistent in mean
-
-
References
[1] J. A. Adam and N. Bellomo, A Survey of Models for Tumor-Immune System Dynamics, Boston: Birkhauser, 1997. ISBN 978-1-4612-6408-8. [2] R. C. Augustin, G. M. Delgoffe and Y. G. Najjar, Characteristics of the tumor microenvironment that influence immune cell functions: Hypoxia, Oxidative Stress, Metabolic Alterations, Cancers, 2020, 12(12), 3802. doi: 10.3390/cancers12123802 [3] S. Bhatt, K. A. Sarosiek and I. S. Lossos, Interleukin 21-its potential role in the therapy of B-cell lymphomas, Leukemia Lymphoma, 2017, 58(1), 17–29. doi: 10.1080/10428194.2016.1201568 [4] S. Banerjee and R. Sarkar, Delay-induced model for tumor-immune interaction and control of malignant tumor growth, Biosystems, 2008, 91(1), 268–288. doi: 10.1016/j.biosystems.2007.10.002 [5] L. G. DePillis and A. Radunskaya, A mathematical tumor model with immune resistance and drug therapy: an optimal control approach, J. Theor. Med., 2001, 3(2), 79–100. doi: 10.1080/10273660108833067 [6] W. Guo and D. Mei, Stochastic resonance in a tumor-immune system subject to bounded noises and time delay, Physica A., 2014, 416(2), 90–98. [7] Y. Guo, W. Zhao and X. Ding, Input-to-state stability for stochastic multi-group models with multi-dispersal and time-varying delay, Appl. Math. Comput., 2019, 343, 114–127. [8] C. Ji, D. Jiang and X. Li, Qualitative analysis of a stochastic ration-dependent predator-prey system, J. Comput. Appl. Math., 2011, 235(1), 1326–1341. [9] C. Ji and D. Jiang, Dynamics of a stochastic density dependent predator-prey system with Beddington-DeAngelis functional response, J. Math. Anal. Appl., 2011, 381(1), 441–453. doi: 10.1016/j.jmaa.2011.02.037 [10] C. Ji, The threshold for a stochastic HIV-1 infection model with Beddington-DeAngelis incidence rate, Appl. Math. Model., 2018, 64, 168–184. doi: 10.1016/j.apm.2018.07.031 [11] M. Kudo, Scientific rationale for combined immunotherapy with PD-1/PD-L1 antibodies and VEGF inhibitors in advanced hepatocellular Carcinoma, Cancers, 2020, 12(5), 1089. doi: 10.3390/cancers12051089 [12] D. Kirschner and J. C. Panetta, Modeling immunotherapy of the tumor-immune interaction, J. Math. Biol., 1998, 37(3), 235–252. doi: 10.1007/s002850050127 [13] L. Liu, Y. Cao, C. Chen, et al, Sorafenib blocks the RAF/MEK/ERK pathway, inhibits tumor angiogenesis, and induces tumor cell apoptosis in hepatocellular carcinoma model PLC/PRF/5, Cancer Res., 2006, 66(24), 11851–11858. doi: 10.1158/0008-5472.CAN-06-1377 [14] D. Li and Y. Li, Stochastic responses of tumor-immune system with periodic treatment, Chinese Phys. B., 2017, 26(9), 29–36. [15] D. Li and F. Cheng, Threshold for extinction and survival in stochastic tumor immune system, Commun. Nonlinear Sci., 2017, 51, 1–12. doi: 10.1016/j.cnsns.2017.03.007 [16] M. Liu and K. Wang, Persistence and extinction of a stochastic single-specie model under regime switching in a polluted environment Ⅱ, J. Theor. Biol., 2010, 267(3), 283–291. doi: 10.1016/j.jtbi.2010.08.030 [17] J. Ma, D. Ma and C. Ji, The role of IL-21 in hematological malignancies, Cytokine, 2011, 56(2), 133–139. doi: 10.1016/j.cyto.2011.07.011 [18] G. E. Mahlbacher, K. C. Reihmer and H. B. Frieboes, A mathematical modeling of tumor-immune cell interactions, J. Theor. Biol., 2019, 469, 47–60. doi: 10.1016/j.jtbi.2019.03.002 [19] X. Mao, Stochastic Differential Equations and Their Applications(Second Edition), Chichester: Horwood Publishing, 2007. ISBN 978-1-904275-34-3. [20] X. Mao, G. Marion and E. Renshaw, Environmental Brownian noise suppresses explosions in population dynamics, Stoch. Proc. Appl., 2002, 97(1), 95–110. doi: 10.1016/S0304-4149(01)00126-0 [21] B. Niu, Y. Gou and Y. Du, Hopf bifurcation induced by delay effect in diffusive tumor-immune system, Int. J. Bifurcat. Chaos, 2018, 28(11), 1–14. [22] T. A. Phan and J. P. Paneta, Basic stochastic model for tumor virotherapy, Math. Biosci. Eng., 2020, 17(4), 4271–4294. doi: 10.3934/mbe.2020236 [23] E. Planten, N. Ikeda and S. Watanabe, Stochastic Differential Equations and Diffusion Processes(Second Edition), North-Holland Mathcmnticnl Library, 1989. ISBN 0-444-87378-3. [24] Y. Senbabaoglu, R. S. Gejman, A. G. Winer, et al, Tumor immune microenvironment characterization in clear cell renal cell carcinoma identifies prognostic and immunotherapeutically relevant messenger RNA signatures, Genome Biol., 2016, 17(1), 231. doi: 10.1186/s13059-016-1092-z [25] H. Saito, H. Shibayama, H. Miyoshi, et al, The influence of tumor immune microenvironment and tumor immunity on the pathogenesis, treatment and prognosis of post-transplant lymphoproliferative disorders (ptld), Hematol. Oncol., 2019, 37(S2), 200–201. [26] N. Zhang, J. Lei and W. Li, Hybrid multi-delay impulsive control for synchronisation of multi-links stochastic delayed complex networks with semi-Markov jump, Int. J. Control, 2021. DOI: 10.1080/00207179.2021.1989046. [27] Y. Zhai, P. Wang and H. Su, Stabilization of stochastic complex networks with delays based on completely aperiodically intermittent control, Nonlinear Anal. Hybri., 2021, 42, 101074. [28] H. Zhou, Q. Jiang, W. Li, et al, Stability of stochastic Lévy noise coupled systems with mixed delays, Int. J. Control, 2022, 95(1), 234–248. -
-
Figures(4)
Export File
Citation
Jingnan Wang, Shengnan Liu. PERSISTENCE AND EXTINCTION OF THE TUMOR-IMMUNE STOCHASTIC MODEL WITH EFFECTOR CELLS AND CYTOKINES[J]. Journal of Applied Analysis & Computation, 2023, 13(2): 655-670. doi: 10.11948/20210464
Format
Content
DownLoad:
-
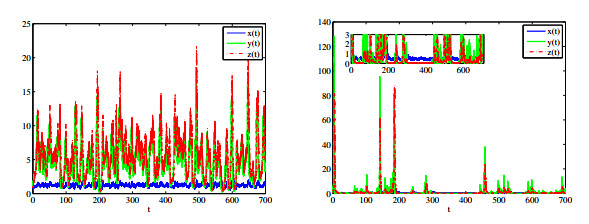
Figure 1.
Waveform plots of effector cell
$ x(t) $ $ y(t) $ $ z(t) $ $ \rho_{i}=0, i=1, 2, 3 $ $ \rho_{1}=0.1, \rho_{2}=1.15, \rho_{3}=0.1 $ -
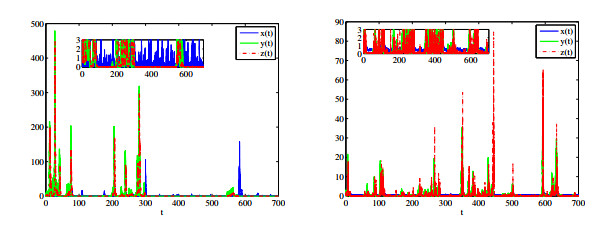
Figure 2.
Waveform plots of effector cell
$ x(t) $ $ y(t) $ $ z(t) $ $ \rho_{1}=0.1, \rho_{3}=0.1 $ $ \rho_{2}=0.1 $ $ \rho_{2}=0.7 $ -
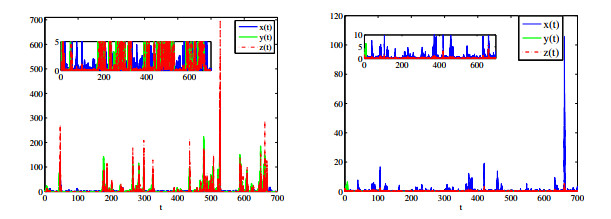
Figure 3.
Waveform plots of effector cell
$ x(t) $ $ y(t) $ $ z(t) $ $ \rho_{2}=0.7 $ $ \rho_{1}=1.15, \rho_{3}=0.1 $ $ \rho_{1}=0.1, \rho_{3}=1.15 $ -
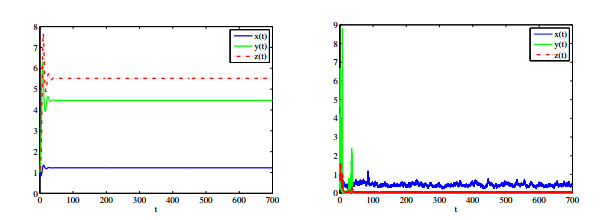
Figure 4.
Waveform plots of effector cell
$ x(t) $ $ y(t) $ $ z(t) $ $ \rho_{1}=1.15, \rho_{3}=1.15 $ $ \rho_{2}=0.7 $ $ \rho_{2}=1.15 $