| Citation: |
Ming Kang, Fengjie Geng, Ming Zhao. DYNAMICAL BEHAVIORS OF A STOCHASTIC PREDATOR-PREY MODEL WITH ANTI-PREDATOR BEHAVIOR[J]. Journal of Applied Analysis & Computation, 2023, 13(3): 1209-1224. doi: 10.11948/20210497
|
DYNAMICAL BEHAVIORS OF A STOCHASTIC PREDATOR-PREY MODEL WITH ANTI-PREDATOR BEHAVIOR
-
Abstract
In this paper, a stochastic predator-prey model is proposed and studied, where the model has anti-predator behavior. By constructing a suitable Lyapunov function, combined with the Itô's formula and the stochastic comparison theorem, the existence and uniqueness of the global positive solution of the system are proved. Then the stochastic boundedness of the system is established, and we discussed the asymptotic behavior of the solution which fluctuates around the equilibrium point of the deterministic model. Moreover, we provide sufficient conditions for the persistence and extinction of the predator and prey. Finally, the results obtained in this paper are verified by numerical simulation, and the anti-predator behavior and stochastic perturbation are analyzed as well.
-
Keywords:
- Stochastic predator-prey model /
- anti-predator behavior /
- boundedness /
- persistence /
- extinction
-
-
References
[1] J. Bao and J. Shao, Permanence and extinction of regime-switching predator-prey models, SIAM Journal on Mathematical Analysis, 2016, 48(1), 725–739. doi: 10.1137/15M1024512 [2] Y. Choh, M. Ignacio, M. W. Sabelis and A. Janssen, Predator-prey role reversals, juvenile experience and adult antipredator behaviour, Scientific Reports, 2012, 2. [3] T. C. Gard, Persistence in stochastic food web models, Bulletin of Mathematical Biology, 1984, 46(3), 357–370. doi: 10.1016/S0092-8240(84)80044-0 [4] T. C. Gard, Stability for multispecies population models in random environments, Nonlinear Analysis: Theory, Methods & Applications, 1986, 10(12), 1411–1419. [5] L. Imhof and S. Walcher, Exclusion and persistence in deterministic and stochastic chemostat models, Journal of Differential Equations, 2005, 217(1), 26–53. doi: 10.1016/j.jde.2005.06.017 [6] C. Ji, D. Jiang and X. Li, Qualitative analysis of a stochastic ratio-dependent predator-prey system, Journal of Computational and Applied Mathematics, 2011, 235(5), 1326–1341. doi: 10.1016/j.cam.2010.08.021 [7] K$\breve{r}$ivan and Vlastimil, Effects of optimal antipredator behavior of prey on predator–prey dynamics: The role of refuges, Theoretical Population Biology, 1998, 53(2), 131–142. doi: 10.1006/tpbi.1998.1351 [8] K. Kiss and S. Kovács, Qualitative behavior of n-dimensional ratio-dependent predator–prey systems, Applied Mathematics and Computation, 2008, 199(2), 535–546. doi: 10.1016/j.amc.2007.10.019 [9] H. Li and F. Cong, Dynamics of a stochastic holling–tanner predator–prey model, Physica A: Statistical Mechanics and its Applications, 2019, 531, 121761. doi: 10.1016/j.physa.2019.121761 [10] Q. Liu, D. Jiang, T. Hayat and A. Alsaedi, Stationary distribution and extinction of a stochastic predator–prey model with herd behavior, Journal of the Franklin Institute, 2018, 355(16), 8177–8193. doi: 10.1016/j.jfranklin.2018.09.013 [11] R. Liu and G. Liu, Dynamics of a stochastic three species prey-predator model with intraguild predation, Journal of Applied Analysis & Computation, 2020, 10(1), 81–103. [12] X. Liu and L. Chen, Complex dynamics of holling type ii lotka–volterra predator–prey system with impulsive perturbations on the predator, Chaos, Solitons & Fractals, 2003, 16(2), 311–320. [13] A. J. Lotka, Contribution to the theory of periodic reactions, The Journal of Physical Chemistry, 1910, 14(3), 271–274. doi: 10.1021/j150111a004 [14] J. Lv, H. Liu and X. Zou, Stationary distribution and persistence of a stochastic predator-prey model with a functional response, Journal of Applied Analysis & Computation, 2020, 10(4), 1242–1255. [15] J. Lv, X. Zou and Y. Li, Dynamical properties of a stochastic predator-prey model with functional response, Journal of Applied Analysis & Computation, 2020, 10(4), 1242–1255. [16] X. Mao, Stochastic Differential Equations and Applications (Second Edition), Woodhead Publishing, UK, 2011. [17] S. N. Raw, P. Mishra and B. Tiwari, Mathematical study about a predator–prey model with anti-predator behavior, International Journal of Applied and Computational Mathematics, 2020, 6(3), 68. doi: 10.1007/s40819-020-00822-5 [18] X. Sun, Y. Li and Y. Xiao, A predator–prey model with prey population guided anti-predator behavior, International Journal of Bifurcation and Chaos, 2017, 27(07), 1750099. doi: 10.1142/S0218127417500997 [19] B. Tang and Y. Xiao, Bifurcation analysis of a predator–prey model with anti-predator behaviour, Chaos, Solitons & Fractals, 2015, 70, 58–68. [20] V. Volterra, Variazioni e fluttuazioni del numero d"individui in specie animali conviventi, Memoria della Reale Accademia Nazionale dei Lincei, 1926, vol. 2, 31–113. [21] L. Wang, M. Zhang and M. Jia, A delayed predator-prey model with pery populationguided anti-predator behaviour and stage structure, Journal of Applied Analysis & Computation, 2021, 11(4), 1811–1824. [22] X. Zhao and Z. Zeng, Stationary distribution of a stochastic predator–prey system with stage structure for prey, Physica A: Statistical Mechanics and its Applications, 2020, 545, 123318. doi: 10.1016/j.physa.2019.123318 [23] Y. Zhao and D. Jiang, The threshold of a stochastic sis epidemic model with vaccination, Applied Mathematics and Computation, 2014, 243, 718–727. doi: 10.1016/j.amc.2014.05.124 -
-
Figures(7)
Export File
Citation
Ming Kang, Fengjie Geng, Ming Zhao. DYNAMICAL BEHAVIORS OF A STOCHASTIC PREDATOR-PREY MODEL WITH ANTI-PREDATOR BEHAVIOR[J]. Journal of Applied Analysis & Computation, 2023, 13(3): 1209-1224. doi: 10.11948/20210497
Format
Content
DownLoad:
-
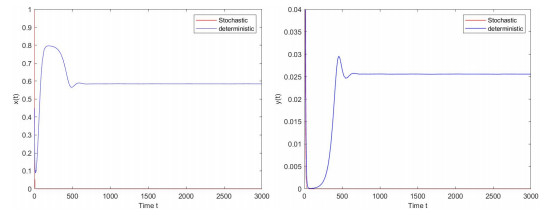
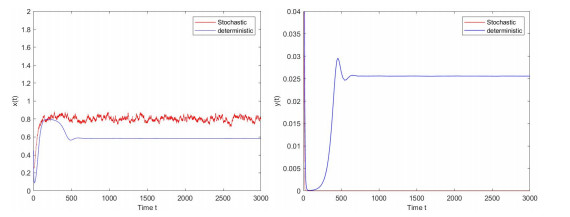
Figure 1.
the paths of the populations
$ x(t) $ $ y(t) $ $ \sigma_{1}=0.01, \sigma_{2}=0.01 $ -
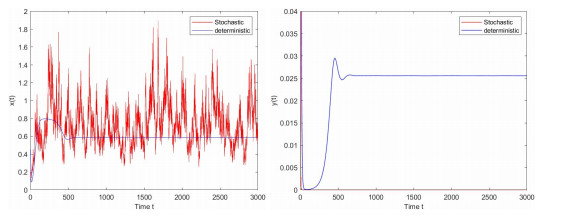
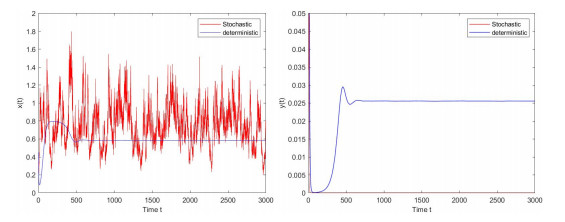
Figure 2.
the paths of the populations
$ x(t) $ $ y(t) $ $ \sigma_{1}=0.9, \sigma_{2}=0.01 $ -
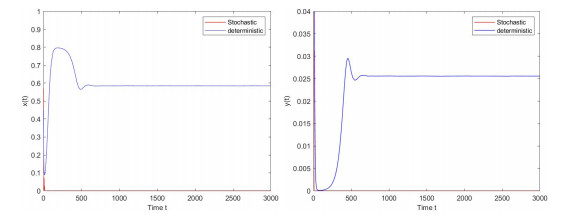
Figure 3.
the paths of the populations
$ x(t) $ $ y(t) $ $ \sigma_{1}=0.1, \sigma_{2}=1.2 $ -
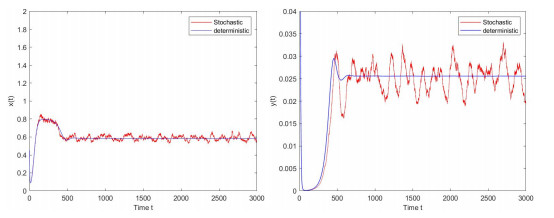
Figure 4.
the paths of the populations
$ x(t) $ $ y(t) $ $ \sigma_{1}=0.8, \sigma_{2}=1.1 $ -
Figure 5.
the paths of the populations
$ x(t) $ $ y(t) $ $ \sigma_{1}=0.01, \sigma_{2}=0.01, \eta=0.01 $ -
Figure 6.
the paths of the populations
$ x(t) $ $ y(t) $ $ \eta=0.8, \sigma_{1}=0.01, \sigma_{2}=0.01 $ -
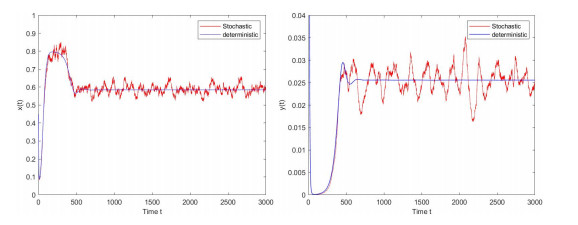
Figure 7.
the paths of the populations
$ x(t) $ $ y(t) $ $ \eta=0.8, \sigma_{1}=0.1, \sigma_{2}=0.3 $