| Citation: |
Jian-Guo Liu, Abdul-Majid Wazwaz, Run-Fa Zhang, Zhong-Zhou Lan, Wen-Hui Zhu. BREATHER-WAVE, MULTI-WAVE AND INTERACTION SOLUTIONS FOR THE (3+1)-DIMENSIONAL GENERALIZED BREAKING SOLITON EQUATION[J]. Journal of Applied Analysis & Computation, 2022, 12(6): 2426-2440. doi: 10.11948/20210507
|
BREATHER-WAVE, MULTI-WAVE AND INTERACTION SOLUTIONS FOR THE (3+1)-DIMENSIONAL GENERALIZED BREAKING SOLITON EQUATION
-
Abstract
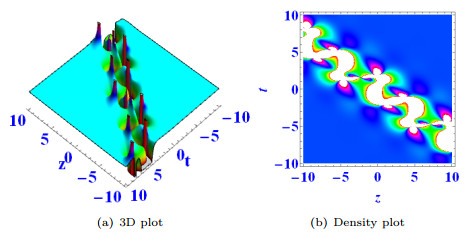
In this paper, a (3+1)-dimensional generalized breaking soliton equation in nonlinear media is investigated. The interaction solution between lump wave and N-soliton (N=2, 3, 4) are derived. The interaction solution between lump wave and periodic waves is also studied. Breather-wave and multi-wave solutions are obtained. The dynamical behavior is demonstrated by some 3D graphics and density plots. Via means of mathematical induction, we also obtain the exact solution containing three arbitrary functions.
-
-
References
[1] K. Aasma, R. Akmal, S. N. Kottakkaran, et al., Splines solutions of boundary value problems that arises in sculpturing electrical process of motors with two rotating mechanism circuit, Phys. Scripta, 2021, 96(10), 104001. [2] Z. Asim, R. Muhammad, Q. Z. Muhammad, et al., Dynamics of Different Nonlinearities to the Perturbed Nonlinear Schrödinger Equation via Solitary Wave Solutions with Numerical Simulation, Fractal Fract., 2021, 5(4), 213. [3] I. Bilge, M. S. Osman, A. Turgut, et al., Analytical and numerical solutions of mathematical biology models: The Newell-Whitehead-Segel and Allen-Cahn equations, Math. Method. Appl. Sci., 2020, 43(5), 2588–2600. doi: 10.1002/mma.6067 [4] W. Cheng, B. Li and Y. Chen, Construction of Soliton-Cnoidal Wave Interaction Solution for the (2+1)-Dimensional Breaking Soliton Equation, Commun. Theor. Phys., 2015, 63(5), 549–553. doi: 10.1088/0253-6102/63/5/549 [5] M. T. Darvishi and M. Najafi, Some exact solutions of the (2+1)-dimensional breaking soliton equation using the three-wave method, Int. J. Comput. Math. Sci., 2012, 6, 13–16. [6] Y. Fan and A. Chen, Lump and interactional solutions of the (2+1)-dimensional generalized breaking soliton equation, Mod. Phys. Lett. B, 2020, 34(3), 2050037. [7] J. Fei and W. Gao, Lie symmetries and invariant solutions of (2+1)-dimensional breaking soliton equation, Wave. Random Complex, 2020, 30(1), 54–64. [8] L. Gai, W. Ma and M. Li, Lump-type solutions, rogue wave type solutions and periodic lump-stripe interaction phenomena to a (3+1)-dimensional generalized breaking soliton equation, Phys. Lett. A, 2020, 384(8), 126178. doi: 10.1016/j.physleta.2019.126178 [9] L. Gao, Y. Zi, Y. Yin, et al., Bäcklund transformation, multiple wave solutions and lump solutions to a (3 + 1)-dimensional nonlinear evolution equation, Nonlinear Dyn., 2017, 89, 2233–2240. [10] H. Hao, D. Zhang, J. Zhang, et al., Rational and Periodic Solutions for a (2+1)-Dimensional Breaking Soliton Equation Associated with ZS-AKNS Hierarchy, Commun. Theor. Phys., 2010, 53(3), 430–434. [11] K. Hosseini, A. R. Seadawy, M. Mirzazadeh, et al., Multiwave, multicomplexiton, and positive multicomplexiton solutions to a (3+1)-dimensional generalized breaking soliton equation, Alex. Eng. J., 2020, 59, 3473–3479. [12] S. Imran, M. M. J. Mohammed, Z. Asim, et al., Exact traveling wave solutions for two prolific conformable M-Fractional differential equations via three diverse approaches, Results Phys., 2021, 28, 104557. [13] Y. Jiang, D. Xian and X. Kang, Homoclinic breather and rogue wave solutions to Maccari equation, Comput. Math. Appl., 2020, 79(7), 1890–1894. [14] B. Kaur and R. K. Gupta, Time fractional (2+1)-dimensional Wu-Zhang system: Dispersion analysis, similarity reductions, conservation laws, and exact solutions, Comput. Math. Appl., 2020, 79(4), 1031–1048. [15] K. A. Karmina, Y. Resat and M. S. Osman, Dynamic behavior of the (3+1)-dimensional KdV-Calogero-Bogoyavlenskii-Schiff equation, Opt. Quant. Electron., 2022, 54(3), 160. [16] H. Li, X. Wan, Z. Fu, et al., New special structures to the (2+1)-dimensional breaking soliton equations, Phys. Scr., 2011, 84, 035005. [17] J. Liu, W. Zhu, M. S. Osman, et al., An explicit plethora of different classes of interactive lump solutions for an extension form of 3D-Jimbo-Miwa model, Eur. Phys. J. Plus, 2020, 135(5), 412. [18] Z. Lan and J. Su, Solitary and rogue waves with controllable backgrounds for the non-autonomous generalized AB system, Nonlinear Dyn., 2019, 96, 2535–2546. [19] W. Ma, Y. Zhang and Y. Tang, Symbolic Computation of Lump Solutions to a Combined Equation Involving Three Types of Nonlinear Terms, East Asian J. Appl. Math., 2020, 10(4), 732–745. [20] W. Ma, Type (−λ, −λ*) reduced nonlocal integrable mKdV equations and their soliton solutions, Appl. Math. Lett., 2022, 131, 108074. [21] W. Ma, Riemann-Hilbert Problems and Soliton Solutions of Type (−λ, −λ*) Reduced Nonlocal Integrable mKdV Hierarchies, Mathematics, 2022, 10(6), 870. [22] W. Ma, Nonlocal integrable mKdV equations by two nonlocal reductions and their soliton solutions, J. Geom. Phys., 2022, 177, 104522. [23] W. Ma, N-soliton solution and the Hirota conditions in (2+1)-dimensions, Opt. Quant. Electron., 2020, 52, 511. [24] W. Ma, N-soliton solutions and the Hirota conditions in (1+1)-dimensions, Int. J. Nonlinear Sci. Numer. Simul., 2022, 23(1), 123–133. [25] W. Ma, X. Yong and X. Lü, Soliton solutions to the B-type Kadomtsev-Petviashvili equation under general dispersion relations, Wave Motion, 2021, 103, 102719. [26] W. Ma, N-soliton solution of a combined pKP-BKP equation, J. Geom. Phys., 2021, 165, 104191. [27] W. Ma, N-soliton solution and the Hirota condition of a (2+1)-dimensional combined equation, Math. Comput. Simul., 2021, 190, 270–279. [28] H. Naher and F. A. Abdullah, The improved (G'/G)-expansion method to the (2+1)-dimensional breaking soliton equation, J. Comput. Anal. Appl., 2014, 16(2), 220–235. [29] M. S. Osman, On multi-soliton solutions for the (2+1)-dimensional breaking soliton equation with variable coefficients in a graded-index waveguide, Comput. Math. Appl., 2018, 75(1), 1–6. [30] A. A. Omar, A. S. Mohammed, A. Hassan, et al., A novel analytical algorithm for generalized fifth-order time-fractional nonlinear evolution equations with conformable time derivative arising in shallow water waves, Alex. Eng. J., 2022, 61(7), 5753–5769. [31] B. Qin, B. Tian, L. Liu, et al., Bäcklund Transformation and Multisoliton Solutions in Terms of Wronskian Determinant for (2+1)-Dimensional Breaking Soliton Equations with Symbolic Computation, Commun. Theor. Phys., 2010, 12, 1059–1066. [32] J. Su and S. Zhang, Nth-order rogue waves for the AB system via the determinants, Appl. Math. Lett., 2021, 112, 106714. [33] J. Su, Y. Gao, G. Deng, et al., Solitary waves, breathers, and rogue waves modulated by long waves for a model of a baroclinic shear flow, Phys. Rev. E, 2019, 100, 042210. [34] T. Sibel, K. A. Karmina, T. Sun, et al., Nonlinear pulse propagation for novel optical solitons modeled by Fokas system in monomode optical fibers, Results Phys., 2022, 36, 105381. [35] K. Sachin, K. D. Shubham, B. Dumitru, et al., Lie Symmetries, Closed-Form Solutions, and Various Dynamical Profiles of Solitons for the Variable Coefficient (2+1)-Dimensional KP Equations, Symmetry, 2022, 14(3), 597. [36] A. M. Wazwaz, A (2+1)-dimensional time-dependent Date-Jimbo-Kashiwara-Miwa equation: Painlevé integrability and multiple soliton solutions, Comput. Math. Appl., 2020, 79(4), 1145–1149. [37] X. Wu, B. Tian, Q. Qu, et al., Rogue waves for a (2+1)-dimensional Gross-Pitaevskii equation with time-varying trapping potential in the Bose-Einstein condensate, Comput. Math. Appl., 2020, 79(4), 1023–1030. [38] M. Wang, B. Tian, Y. Sun, et al., Lump, mixed lump-stripe and rogue wave-stripe solutions of a (3+1)-dimensional nonlinear wave equation for a liquid with gas bubbles, Comput. Math. Appl., 2020, 79(3), 576–587. [39] A. M. Wazwaz, A New Integrable (2+1)-Dimensional Generalized Breaking Soliton Equation: N-Soliton Solutions and Traveling Wave Solutions, Commun. Theor. Phys., 2016, 66(4), 385–388. [40] G. Xu and A. M. Wazwaz, Characteristics of integrability, bidirectional solitons and localized solutions for a (3+1)-dimensional generalized breaking soliton equation, Nonlinear Dyn., 2019, 96(3), 1989–2000. [41] J. Yu, B. Ren, J. Wang, et al., Finite Symmetry Transformation Groups and Exact Solutions of Three Generalized Breaking Soliton Equations, Chinese J. Phys., 2013, 51(4), 657–664. [42] C. Yue, A. Elmoasry, M. M. A. Khater, et al., complex wave structures related to the nonlinear long-short wave interaction system: Analytical and numerical techniques, AIP Adv., 2020, 10(4), 045212. [43] Y. Yin, W. Ma, J. Liu, et al., Diversity of exact solutions to a (3+1)-dimensional nonlinear evolution equation and its reduction, Comput. Math. Appl., 2018, 76, 1275–1283. [44] P. Zhang, New exact solutions to breaking soliton equations and Whitham-Broer-Kaup equations, Appl. Math. Comput., 2010, 217(4), 1688–1696. [45] Z. Zhao and L. He, Bäcklund transformations and Riemann-Bäcklund method to a (3+1)-dimensional generalized breaking soliton equation, Eur. Phys. J. Plus, 2020, 135(8), 639. -
-
Figures(9)
Export File
Citation
Jian-Guo Liu, Abdul-Majid Wazwaz, Run-Fa Zhang, Zhong-Zhou Lan, Wen-Hui Zhu. BREATHER-WAVE, MULTI-WAVE AND INTERACTION SOLUTIONS FOR THE (3+1)-DIMENSIONAL GENERALIZED BREAKING SOLITON EQUATION[J]. Journal of Applied Analysis & Computation, 2022, 12(6): 2426-2440. doi: 10.11948/20210507
Format
Content
DownLoad:
-
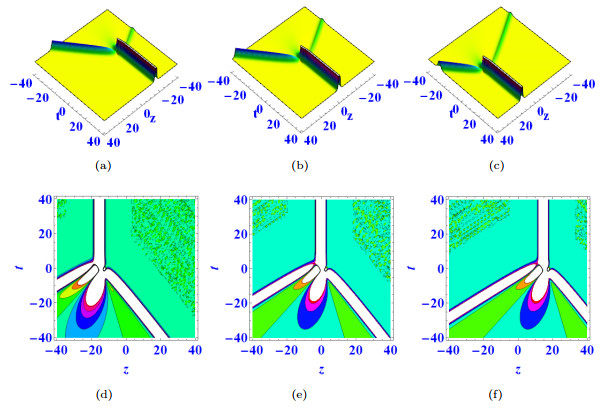
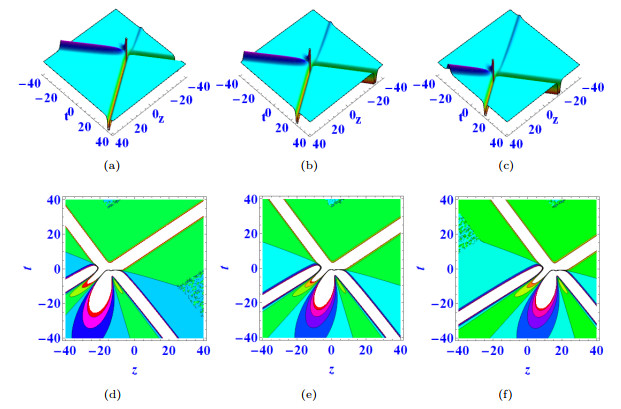
Figure 1.
$ \mathcal{G}_1= \mathcal{G}_5= \mathcal{G}_{11}=\alpha=a_1=d_1=d_2=e_1=k_1=k_2=1 $ ,$ \mathcal{G}_4=\mathcal{G}_9=-1 $ ,$ \mathcal{G}_6=-3 $ ,$ \beta=3 $ ,$ \mathcal{G}_{10}=a_2=k_{12}=-2 $ ,$ e_2=2 $ ,$ y=0 $ , when$ x=-10 $ in (a) (d),$ x=0 $ in (b) (e),$ x=10 $ in (c) (f). -
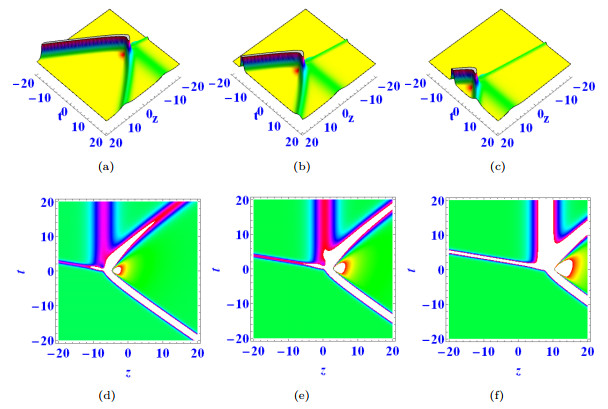
Figure 2.
$ \mathcal{G}_1= \mathcal{G}_5= \mathcal{G}_{11}=\alpha=a_1=d_1=d_2=e_1=k_1=k_2=1 $ ,$ \mathcal{G}_4=\mathcal{G}_9=-1 $ ,$ \mathcal{G}_6=-3 $ ,$ \beta=3 $ ,$ \mathcal{G}_{10} =a_2=-2 $ ,$ e_2=2 $ ,$ y=k_{12}=0 $ , when$ x=-10 $ in (a) (d),$ x=0 $ in (b) (e),$ x=10 $ in (c) (f). -
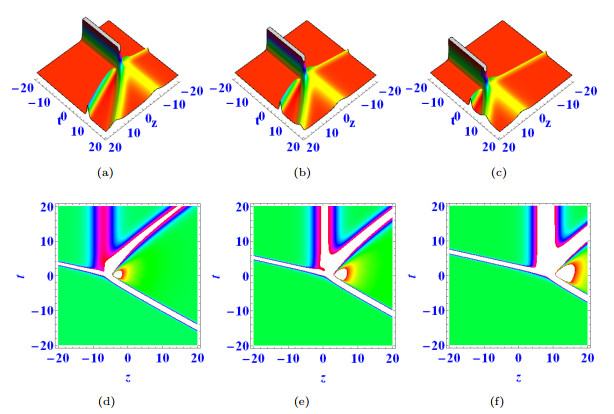
Figure 3.
$ \mathcal{G}_1= \mathcal{G}_5= \mathcal{G}_{11}=\alpha=a_1=d_1=d_2=e_1=1 $ ,$ k_1=e_3=4 $ ,$ \mathcal{G}_{10} =-2 $ ,$ \mathcal{G}_4=\mathcal{G}_9=-1 $ ,$ \mathcal{G}_6=d_3=-3 $ ,$ \beta=a_3=k_3=3 $ ,$ a_2=e_2=k_2=2 $ ,$ y=0 $ , when$ x=-5 $ in (a) (d),$ x=0 $ in (b) (e),$ x=5 $ in (c) (f). -
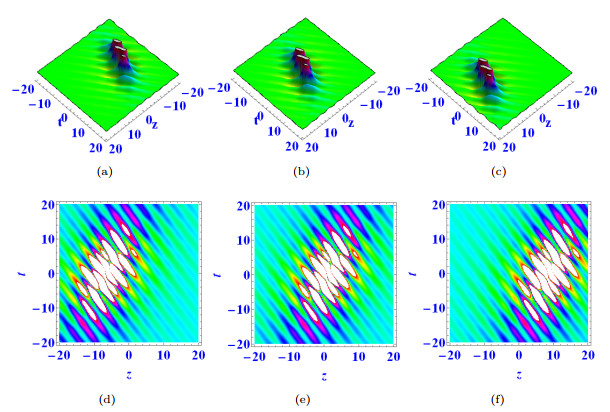
Figure 4.
$ \mathcal{G}_1= \mathcal{G}_5= \mathcal{G}_{11}=\alpha=a_1=d_1=d_2=e_1=1 $ ,$ k_1=e_3=4 $ ,$ k_4=6 $ ,$ y=0 $ ,$ a_2=e_2=k_2=2 $ ,$ \mathcal{G}_4=\mathcal{G}_9=e_4=-1 $ ,$ \mathcal{G}_6=d_3=d_4=-3 $ ,$ \beta=a_3=k_3=3 $ ,$ \mathcal{G}_{10} =a_4=-2 $ , when$ x=-5 $ in (a) (d),$ x=0 $ in (b) (e),$ x=5 $ in (c) (f). -
Figure 5.
$ \mathcal{G}_1= \mathcal{G}_5= \alpha=a_1=d_1=d_2=e_1=1 $ ,$ \mathcal{G}_{11}=10 $ ,$ \mathcal{G}_4=\mathcal{G}_9=-1 $ ,$ \mathcal{G}_6=-3 $ ,$ \beta=3 $ ,$ \mathcal{G}_{10} =a_2=-2 $ ,$ e_2=k_1=2 $ ,$ k_2=6 $ ,$ y=0 $ , when$ x=-5 $ in (a) (d),$ x=0 $ in (b) (e),$ x=5 $ in (c) (f). -
Figure 6.
$ k_1=d_4=-1 $ ,$ a_1=\alpha=a_2=d_2=d_3=1 $ ,$ \beta=3 $ ,$ a_3=-2 $ ,$ k_2=-6 $ ,$ k_3=2 $ ,$ x=y=0 $ . -
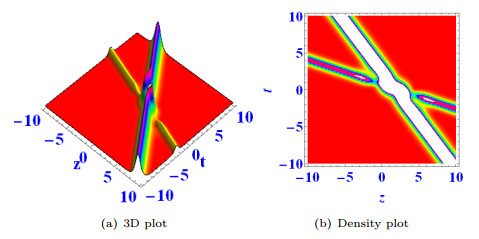
Figure 7.
$ k_1=k_2=k_3=a_1=\alpha=a_1=d_1=d_2=e_1=1 $ ,$ \beta=a_3=3 $ ,$ e_3=4 $ ,$ a_2=e_2=2 $ ,$ d_3=-3 $ ,$ x=y=0 $ . -
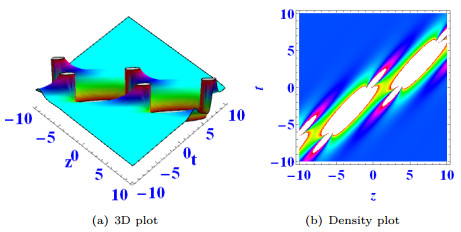
Figure 8.
$ k_1=a_1=\alpha=a_1=d_1=d_2=e_1=1 $ ,$ \beta=a_3=3 $ ,$ d_3=-3 $ ,$ e_3=4 $ ,$ a_2=e_2=k_2=2 $ ,$ x=y=k_3=0 $ . -
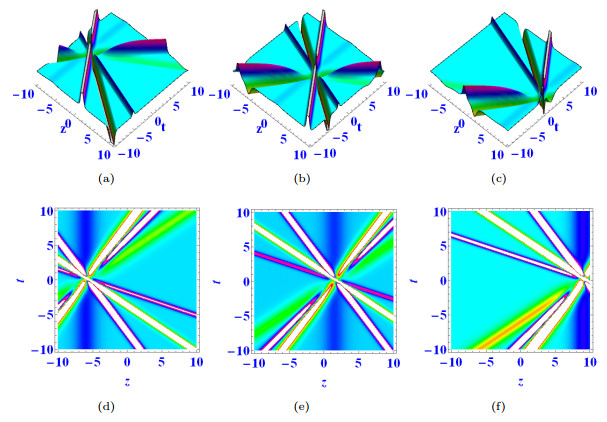
Figure 9.
$ k_1=k_2=k_3=a_1=\alpha=a_1=d_1=d_2=e_1=1 $ ,$ \beta=a_3=3 $ ,$ e_3=4 $ ,$ a_2=e_2=2 $ ,$ d_3=-3 $ ,$ y=0 $ , when$ x=-5 $ in (a) (d),$ x=0 $ in (b) (e),$ x=5 $ in (c) (f).